Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 86, 87, 88 của sách giáo khoa Toán 12 tập 1.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi sắp tới.
Dưới đây là bảng số liệu ghép nhóm về khối lượng 100 quả dứa mà người ta lấy ngẫu nhiên trong số dứa đã thu hoạch
Trả lời câu hỏi Hoạt động 1 trang 86 SGK Toán 12 Cùng khám phá
Dưới đây là bảng số liệu ghép nhóm về khối lượng 100 quả dứa mà người ta lấy ngẫu nhiên trong số dứa đã thu hoạch:
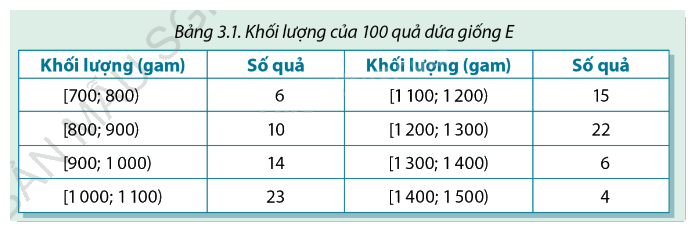
Khối lượng của quả nặng nhất và quả nhẹ nhất có thể chênh lệch nhau nhiều nhất là bao nhiêu?
Phương pháp giải:
- Tìm khoảng khối lượng nhỏ nhất và khoảng khối lượng lớn nhất trong bảng số liệu.
- Xác định giá trị khối lượng cực đại và cực tiểu.
- Tính chênh lệch lớn nhất.
Lời giải chi tiết:
Bảng số liệu ghép nhóm có các khoảng khối lượng như sau:
- Khoảng nhỏ nhất: [700; 800).
- Khoảng lớn nhất: [1400; 1500).
Khối lượng nhẹ nhất có thể nằm trong khoảng nhỏ nhất [700; 800), tức là giá trị nhỏ nhất có thể là 700gram.
Khối lượng nặng nhất có thể nằm trong khoảng lớn nhất [1400; 1500), tức là giá trị lớn nhất có thể là 1500 gram.
Vậy, chênh lệch lớn nhất giữa khối lượng của quả nặng nhất và quả nhẹ nhất là: 1500−700=800 gram.
Do đó, khối lượng chênh lệch lớn nhất giữa quả dứa nặng nhất và quả dứa nhẹ nhất có thể là 800 gram.
Trả lời câu hỏi Luyện tập 2 trang 88 SGK Toán 12 Cùng khám phá
Người ta tiến hành phỏng vấn hai nhóm khán giả về một bộ phim mới công chiếu. Nhóm A gồm những khán giả thuộc lứa tuổi 20 – 30, nhóm B thuộc lứa tuổi trên 30. Người được hỏi ý kiến phải đánh giá bộ phim bằng cách cho điểm theo một số tiêu chí nêu trong phiếu điều tra và sau đó lấy tổng số điểm (thang điểm 100). Bảng dưới đây trình bày kết quả điều tra hai nhóm khán giả:
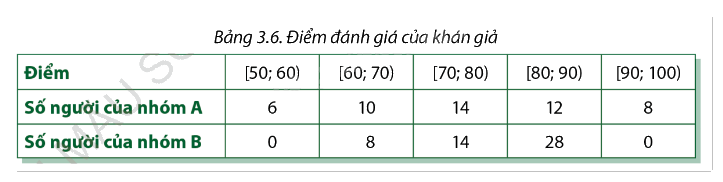
Ý kiến đánh giá của nhóm khán giả nào phân tán hơn?
Phương pháp giải:
So sánh khoảng biến thiên của điểm đánh giá từ số người nhóm A với khoảng biến thiên điểm của điểm đánh giá từ số người nhóm B. Khoảng biến thiên của nhóm nào lớn hơn thì ý kiến đánh giá của nhóm khán giả đó phân tán hơn.
Lời giải chi tiết:
Ý kiến đánh giá của nhóm khán giả A và B lần lượt có khoảng biến thiên tương ứng là: \({R_A} = 100 - 50 = 50;{R_B} = 90 - 60 = 30\).
Vì \({R_A} > {R_B}\) nên ý kiến đánh giá của nhóm khán giả A phân tán hơn so với nhóm khán giả B.
Trả lời câu hỏi Luyện tập 1 trang 87 SGK Toán 12 Cùng khám phá
Bảng 3.4 thống kê thành tích nhảy xa của một số học sinh lớp 12. Tìm khoảng biến thiên thành tích nhảy xa của số học sinh này.

Phương pháp giải:
- Xác định giá trị đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên.
- Tính hiệu số giữa hai đầu mút này.
Lời giải chi tiết:
Đầu mút phải của nhóm ghép cuối cùng là 300, đầu mút trái của nhóm ghép đầu tiên là 150. Vậy khoảng biến thiên thành tích nhảy xa của số học sinh này là: R = 300 – 150 = 150.
Trả lời câu hỏi Hoạt động 1 trang 86 SGK Toán 12 Cùng khám phá
Dưới đây là bảng số liệu ghép nhóm về khối lượng 100 quả dứa mà người ta lấy ngẫu nhiên trong số dứa đã thu hoạch:
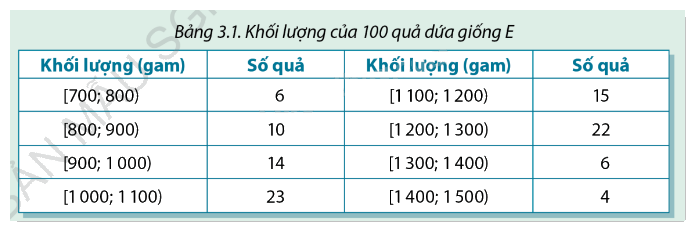
Khối lượng của quả nặng nhất và quả nhẹ nhất có thể chênh lệch nhau nhiều nhất là bao nhiêu?
Phương pháp giải:
- Tìm khoảng khối lượng nhỏ nhất và khoảng khối lượng lớn nhất trong bảng số liệu.
- Xác định giá trị khối lượng cực đại và cực tiểu.
- Tính chênh lệch lớn nhất.
Lời giải chi tiết:
Bảng số liệu ghép nhóm có các khoảng khối lượng như sau:
- Khoảng nhỏ nhất: [700; 800).
- Khoảng lớn nhất: [1400; 1500).
Khối lượng nhẹ nhất có thể nằm trong khoảng nhỏ nhất [700; 800), tức là giá trị nhỏ nhất có thể là 700gram.
Khối lượng nặng nhất có thể nằm trong khoảng lớn nhất [1400; 1500), tức là giá trị lớn nhất có thể là 1500 gram.
Vậy, chênh lệch lớn nhất giữa khối lượng của quả nặng nhất và quả nhẹ nhất là: 1500−700=800 gram.
Do đó, khối lượng chênh lệch lớn nhất giữa quả dứa nặng nhất và quả dứa nhẹ nhất có thể là 800 gram.
Trả lời câu hỏi Luyện tập 1 trang 87 SGK Toán 12 Cùng khám phá
Bảng 3.4 thống kê thành tích nhảy xa của một số học sinh lớp 12. Tìm khoảng biến thiên thành tích nhảy xa của số học sinh này.

Phương pháp giải:
- Xác định giá trị đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên.
- Tính hiệu số giữa hai đầu mút này.
Lời giải chi tiết:
Đầu mút phải của nhóm ghép cuối cùng là 300, đầu mút trái của nhóm ghép đầu tiên là 150. Vậy khoảng biến thiên thành tích nhảy xa của số học sinh này là: R = 300 – 150 = 150.
Trả lời câu hỏi Luyện tập 2 trang 88 SGK Toán 12 Cùng khám phá
Người ta tiến hành phỏng vấn hai nhóm khán giả về một bộ phim mới công chiếu. Nhóm A gồm những khán giả thuộc lứa tuổi 20 – 30, nhóm B thuộc lứa tuổi trên 30. Người được hỏi ý kiến phải đánh giá bộ phim bằng cách cho điểm theo một số tiêu chí nêu trong phiếu điều tra và sau đó lấy tổng số điểm (thang điểm 100). Bảng dưới đây trình bày kết quả điều tra hai nhóm khán giả:
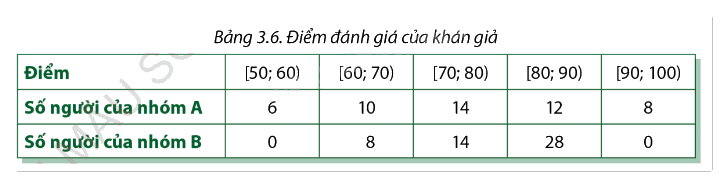
Ý kiến đánh giá của nhóm khán giả nào phân tán hơn?
Phương pháp giải:
So sánh khoảng biến thiên của điểm đánh giá từ số người nhóm A với khoảng biến thiên điểm của điểm đánh giá từ số người nhóm B. Khoảng biến thiên của nhóm nào lớn hơn thì ý kiến đánh giá của nhóm khán giả đó phân tán hơn.
Lời giải chi tiết:
Ý kiến đánh giá của nhóm khán giả A và B lần lượt có khoảng biến thiên tương ứng là: \({R_A} = 100 - 50 = 50;{R_B} = 90 - 60 = 30\).
Vì \({R_A} > {R_B}\) nên ý kiến đánh giá của nhóm khán giả A phân tán hơn so với nhóm khán giả B.
Mục 1 của SGK Toán 12 tập 1 thường tập trung vào các kiến thức nền tảng của một chương mới, thường là về giới hạn, đạo hàm hoặc tích phân. Việc nắm vững kiến thức này là vô cùng quan trọng để giải quyết các bài tập phức tạp hơn trong chương. Các bài tập trang 86, 87, 88 thường bao gồm các dạng bài tập cơ bản để kiểm tra sự hiểu biết của học sinh về các khái niệm và định lý đã học.
Giả sử trang 86 chứa các bài tập về tính giới hạn của hàm số. Chúng ta sẽ bắt đầu bằng việc ôn lại các định nghĩa về giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn thường gặp như phương pháp chia, phương pháp nhân liên hợp, phương pháp sử dụng định lý giới hạn.
Ví dụ, bài tập 1 có thể yêu cầu tính giới hạn: lim (x->2) (x^2 - 4) / (x - 2). Lời giải sẽ là: lim (x->2) (x^2 - 4) / (x - 2) = lim (x->2) (x - 2)(x + 2) / (x - 2) = lim (x->2) (x + 2) = 4.
Trang 87 có thể chứa các bài tập phức tạp hơn về giới hạn, ví dụ như giới hạn vô cùng, giới hạn của hàm số lượng giác. Trong trường hợp này, chúng ta cần sử dụng các định lý giới hạn đặc biệt và các kỹ thuật biến đổi phù hợp.
Ví dụ, bài tập 2 có thể yêu cầu tính giới hạn: lim (x->0) sin(x) / x. Lời giải sẽ là: lim (x->0) sin(x) / x = 1 (Đây là giới hạn lượng giác cơ bản).
Trang 88 thường chứa các bài tập tổng hợp, kết hợp nhiều kiến thức và kỹ năng khác nhau. Việc giải các bài tập này đòi hỏi học sinh phải có khả năng phân tích, tổng hợp và vận dụng linh hoạt các kiến thức đã học.
Ví dụ, bài tập 3 có thể yêu cầu tính giới hạn: lim (x->∞) (2x^2 + 1) / (x^2 + 3). Lời giải sẽ là: lim (x->∞) (2x^2 + 1) / (x^2 + 3) = 2 (Chia cả tử và mẫu cho x^2).
| Công thức | Mô tả |
|---|---|
| lim (x->0) sin(x) / x = 1 | Giới hạn lượng giác cơ bản |
| lim (x->0) (1 - cos(x)) / x = 0 | Giới hạn lượng giác cơ bản |
| lim (x->∞) 1/x = 0 | Giới hạn vô cùng |
Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 86, 87, 88 SGK Toán 12 tập 1. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất trong học tập.