Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 2 trang 68, 69, 70 SGK Toán 12 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải và tự tin làm bài tập.
Cho điểm trong không gian Oxyz. Trong ba mặt phẳng tọa độ là ba lưới ô vuông có cạnh bằng đơn vị. Biết rằng , và vị trí các điểm M’, A, B, C được cho như trong Hình 2.32. a) Biếu diễn theo hai vecto và . b) Biểu diễn theo hai vecto đơn vị . c) Biểu diễn theo ba vectơ dơn vị .
Trả lời câu hỏi Hoạt động 2 trang 68 SGK Toán 12 Cùng khám phá
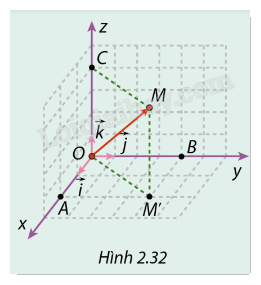
Cho điểm \(M\) trong không gian Oxyz. Trong ba mặt phẳng tọa độ là ba lưới ô vuông có cạnh bằng đơn vị. Biết rằng \(MM' \bot (Oxy)\), \(MC \bot Oz\) và vị trí các điểm M’, A, B, C được cho như trong Hình 2.32.
a) Biểu diễn \(\overrightarrow {OM} \) theo hai vecto \(\overrightarrow {O{M^\prime }} \) và \(\overrightarrow {OC} \).
b) Biểu diễn \(\overrightarrow {O{M^\prime }} \) theo hai vecto đơn vị \(\vec \imath ,\vec \jmath \).
c) Biểu diễn \(\overrightarrow {OM} \) theo ba vectơ dơn vị \(\vec i,\vec j,\vec k\).
Phương pháp giải:
Sử dụng các định nghĩa, các quy tắc về vectơ trong không gian và mối quan hệ trực giao giữa các mặt phẳng tọa độ để biểu diễn các vectơ theo các vectơ đơn vị.
Lời giải chi tiết:
a) Biểu diễn \(\overrightarrow {OM} \) theo hai vectơ \(\overrightarrow {OM'} \) và \(\overrightarrow {OC} \):
Do \(MM' \bot (Oxy)\), \(MC \bot Oz\) nên OCMM’ là hình chữ nhật.
Áp dụng quy tắc hình bình hành vào hình chữ nhật OCMM’, ta có:
\(\overrightarrow {OM} = \overrightarrow {OM'} + \overrightarrow {OC} \)
b) Biểu diễn \(\overrightarrow {OM'} \) theo hai vectơ đơn vị \(\vec i,\vec j\):
Áp dụng quy tắc hình bình hành vào hình chữ nhật OAM’B, ta có:
\(\overrightarrow {OM'} = \overrightarrow {OA} + \overrightarrow {OB} \)
Mà \(\overrightarrow {OA} = 2\overrightarrow i ,\overrightarrow {OB} = 4\overrightarrow j \) nên:
\(\overrightarrow {OM'} = 2\overrightarrow i + 4\overrightarrow j \)
c) Biểu diễn \(\overrightarrow {OM} \) theo ba vectơ đơn vị \(\vec i,\vec j,\vec k\):
Từ câu a, b ta có:
\(\overrightarrow {OM} = \overrightarrow {OM'} + \overrightarrow {OC} \) và \(\overrightarrow {OM'} = 2\overrightarrow i + 4\overrightarrow j \)
Lại có \(\overrightarrow {OC} = 4\overrightarrow k \) nên:
\(\overrightarrow {OM} = 2\vec i + 4\vec j + 4\vec k\)
Trả lời câu hỏi Luyện tập 2 trang 69 SGK Toán 12 Cùng khám phá
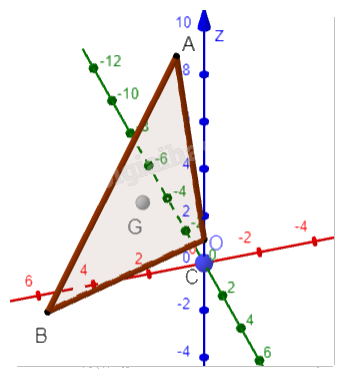
Trong không gian Oxyz, cho ba điểm A(1;0;9), B(6;1;0) và C(0;0;1). Gọi G là trọng tâm của tam giác ABC. Tìm toạ độ điểm G.
Phương pháp giải:
Trọng tâm của tam giác là trung bình cộng tọa độ của ba đỉnh của tam giác. Nếu các đỉnh của tam giác là \(A({x_1},{y_1},{z_1})\), \(B({x_2},{y_2},{z_2})\), và \(C({x_3},{y_3},{z_3})\), tọa độ của trọng tâm G được tính bằng:
\(G\left( {\frac{{{x_1} + {x_2} + {x_3}}}{3},\frac{{{y_1} + {y_2} + {y_3}}}{3},\frac{{{z_1} + {z_2} + {z_3}}}{3}} \right)\)
Lời giải chi tiết:
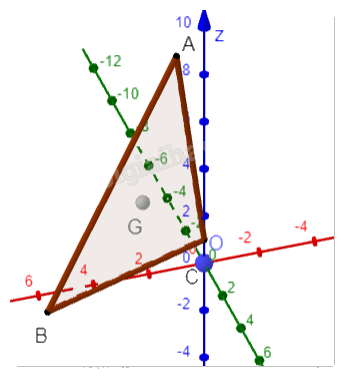
Toạ độ của điểm trọng tâm G là trung bình cộng của toạ độ các điểm A, B, C.
\({x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{1 + 6 + 0}}{3} = \frac{7}{3}\)
\({y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{0 + 1 + 0}}{3} = \frac{1}{3}\)
\({z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{9 + 0 + 1}}{3} = \frac{{10}}{3}\)
Toạ độ của trọng tâm G là: \(G\left( {\frac{7}{3},\frac{1}{3},\frac{{10}}{3}} \right)\)
Trả lời câu hỏi Luyện tập 3 trang 70 SGK Toán 12 Cùng khám phá
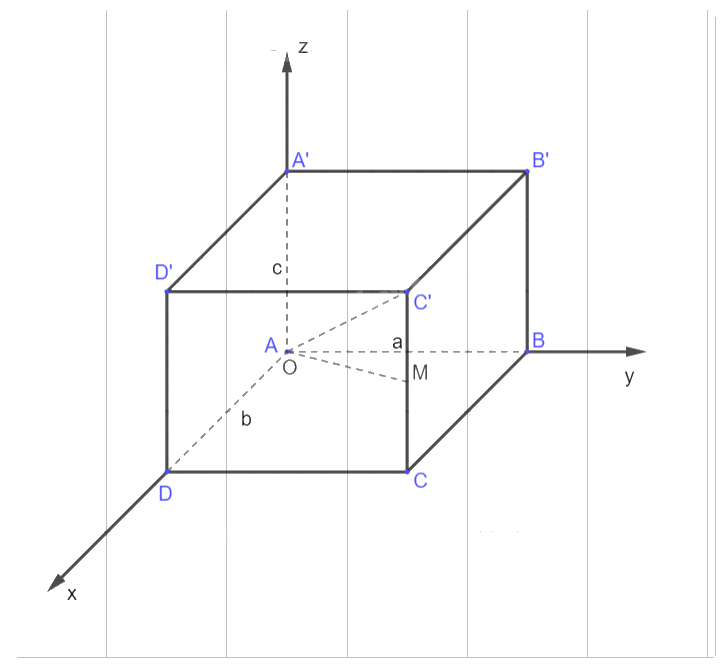
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ có đỉnh A trùng với gốc O, có \[\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {AA'} \] theo thứ tự cùng hướng với các vectơ đơn vị \(\vec i,\vec j,\vec k\) và có \(AB = a,AD = b,AA' = c\). Gọi M là trung điểm cạnh CC’. Hãy xác định toạ độ các điểm B, C, C’ và M.
Phương pháp giải:
Xác định tọa độ điểm cơ bản: Sử dụng các vectơ đơn vị để xác định tọa độ của các điểm quan trọng trong không gian.
Xác định tọa độ các điểm còn lại: Tính tọa độ của các điểm đối diện trong hình hộp dựa trên tọa độ của các điểm đã biết.
Tính tọa độ trung điểm: Sử dụng công thức tính trung điểm để tìm tọa độ của điểm trung gian trên cạnh.
Lời giải chi tiết:
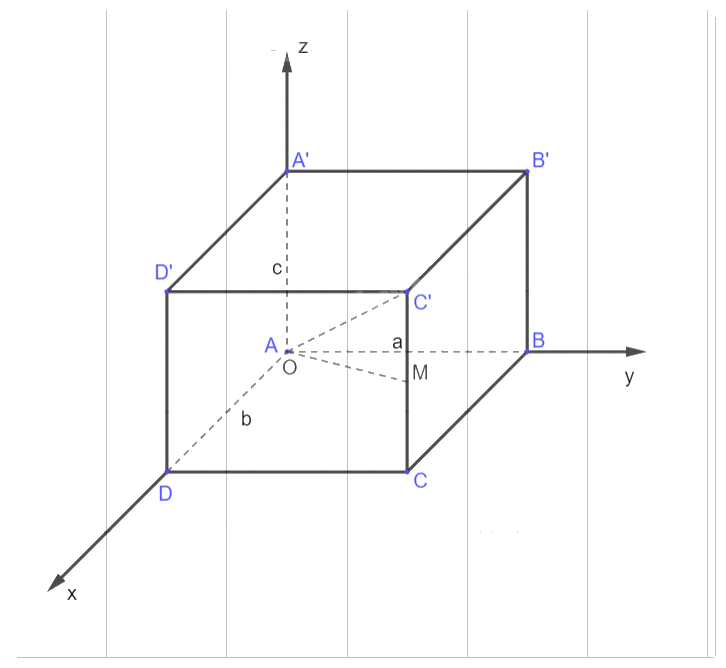
- Xác định tọa độ các điểm cơ bản:
Tọa độ của điểm A là (0, 0, 0) vì A trùng với gốc tọa độ O.
Tọa độ của điểm B: Điểm B nằm cách điểm A một đoạn a theo hướng của vector đơn vị \(\vec i\). Vì vậy, tọa độ của B là (a, 0, 0).
Tọa độ của điểm D: Điểm D nằm cách điểm A một đoạn b theo hướng của vector đơn vị \(\vec j\). Vì vậy, tọa độ của D là (0, b, 0).
Tọa độ của điểm A': Điểm A' nằm cách điểm A một đoạn c theo hướng của vector đơn vị \(\vec k\). Vì vậy, tọa độ của A' là (0, 0, c).
- Xác định tọa độ các điểm còn lại:
Tọa độ của điểm C: Điểm C nằm đối diện với điểm A trong hình hộp và nằm trên mặt phẳng chứa B và D. Vì vậy, tọa độ của C là (a, b, 0).
Tọa độ của điểm C': Điểm C' nằm đối diện với điểm A' trong hình hộp và nằm trên mặt phẳng chứa B' và D'. Vì vậy, tọa độ của C' là (a, b, c).
Trung điểm của đoạn thẳng CC' có tọa độ trung bình của tọa độ C và C'. Tọa độ của C là (a, b, 0) và tọa độ của C' là (a, b, c). Do đó, tọa độ của M là:
\(M = \left( {\frac{{a + a}}{2},\frac{{b + b}}{2},\frac{{0 + c}}{2}} \right) = (a,b,\frac{c}{2})\)
Trả lời câu hỏi Hoạt động 2 trang 68 SGK Toán 12 Cùng khám phá
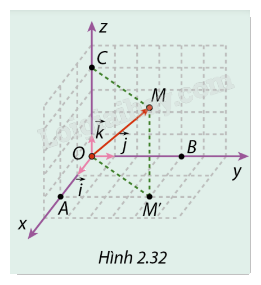
Cho điểm \(M\) trong không gian Oxyz. Trong ba mặt phẳng tọa độ là ba lưới ô vuông có cạnh bằng đơn vị. Biết rằng \(MM' \bot (Oxy)\), \(MC \bot Oz\) và vị trí các điểm M’, A, B, C được cho như trong Hình 2.32.
a) Biểu diễn \(\overrightarrow {OM} \) theo hai vecto \(\overrightarrow {O{M^\prime }} \) và \(\overrightarrow {OC} \).
b) Biểu diễn \(\overrightarrow {O{M^\prime }} \) theo hai vecto đơn vị \(\vec \imath ,\vec \jmath \).
c) Biểu diễn \(\overrightarrow {OM} \) theo ba vectơ dơn vị \(\vec i,\vec j,\vec k\).
Phương pháp giải:
Sử dụng các định nghĩa, các quy tắc về vectơ trong không gian và mối quan hệ trực giao giữa các mặt phẳng tọa độ để biểu diễn các vectơ theo các vectơ đơn vị.
Lời giải chi tiết:
a) Biểu diễn \(\overrightarrow {OM} \) theo hai vectơ \(\overrightarrow {OM'} \) và \(\overrightarrow {OC} \):
Do \(MM' \bot (Oxy)\), \(MC \bot Oz\) nên OCMM’ là hình chữ nhật.
Áp dụng quy tắc hình bình hành vào hình chữ nhật OCMM’, ta có:
\(\overrightarrow {OM} = \overrightarrow {OM'} + \overrightarrow {OC} \)
b) Biểu diễn \(\overrightarrow {OM'} \) theo hai vectơ đơn vị \(\vec i,\vec j\):
Áp dụng quy tắc hình bình hành vào hình chữ nhật OAM’B, ta có:
\(\overrightarrow {OM'} = \overrightarrow {OA} + \overrightarrow {OB} \)
Mà \(\overrightarrow {OA} = 2\overrightarrow i ,\overrightarrow {OB} = 4\overrightarrow j \) nên:
\(\overrightarrow {OM'} = 2\overrightarrow i + 4\overrightarrow j \)
c) Biểu diễn \(\overrightarrow {OM} \) theo ba vectơ đơn vị \(\vec i,\vec j,\vec k\):
Từ câu a, b ta có:
\(\overrightarrow {OM} = \overrightarrow {OM'} + \overrightarrow {OC} \) và \(\overrightarrow {OM'} = 2\overrightarrow i + 4\overrightarrow j \)
Lại có \(\overrightarrow {OC} = 4\overrightarrow k \) nên:
\(\overrightarrow {OM} = 2\vec i + 4\vec j + 4\vec k\)
Trả lời câu hỏi Luyện tập 2 trang 69 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba điểm A(1;0;9), B(6;1;0) và C(0;0;1). Gọi G là trọng tâm của tam giác ABC. Tìm toạ độ điểm G.
Phương pháp giải:
Trọng tâm của tam giác là trung bình cộng tọa độ của ba đỉnh của tam giác. Nếu các đỉnh của tam giác là \(A({x_1},{y_1},{z_1})\), \(B({x_2},{y_2},{z_2})\), và \(C({x_3},{y_3},{z_3})\), tọa độ của trọng tâm G được tính bằng:
\(G\left( {\frac{{{x_1} + {x_2} + {x_3}}}{3},\frac{{{y_1} + {y_2} + {y_3}}}{3},\frac{{{z_1} + {z_2} + {z_3}}}{3}} \right)\)
Lời giải chi tiết:
Toạ độ của điểm trọng tâm G là trung bình cộng của toạ độ các điểm A, B, C.
\({x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{1 + 6 + 0}}{3} = \frac{7}{3}\)
\({y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{0 + 1 + 0}}{3} = \frac{1}{3}\)
\({z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{9 + 0 + 1}}{3} = \frac{{10}}{3}\)
Toạ độ của trọng tâm G là: \(G\left( {\frac{7}{3},\frac{1}{3},\frac{{10}}{3}} \right)\)
Trả lời câu hỏi Luyện tập 3 trang 70 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ có đỉnh A trùng với gốc O, có \[\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {AA'} \] theo thứ tự cùng hướng với các vectơ đơn vị \(\vec i,\vec j,\vec k\) và có \(AB = a,AD = b,AA' = c\). Gọi M là trung điểm cạnh CC’. Hãy xác định toạ độ các điểm B, C, C’ và M.
Phương pháp giải:
Xác định tọa độ điểm cơ bản: Sử dụng các vectơ đơn vị để xác định tọa độ của các điểm quan trọng trong không gian.
Xác định tọa độ các điểm còn lại: Tính tọa độ của các điểm đối diện trong hình hộp dựa trên tọa độ của các điểm đã biết.
Tính tọa độ trung điểm: Sử dụng công thức tính trung điểm để tìm tọa độ của điểm trung gian trên cạnh.
Lời giải chi tiết:
- Xác định tọa độ các điểm cơ bản:
Tọa độ của điểm A là (0, 0, 0) vì A trùng với gốc tọa độ O.
Tọa độ của điểm B: Điểm B nằm cách điểm A một đoạn a theo hướng của vector đơn vị \(\vec i\). Vì vậy, tọa độ của B là (a, 0, 0).
Tọa độ của điểm D: Điểm D nằm cách điểm A một đoạn b theo hướng của vector đơn vị \(\vec j\). Vì vậy, tọa độ của D là (0, b, 0).
Tọa độ của điểm A': Điểm A' nằm cách điểm A một đoạn c theo hướng của vector đơn vị \(\vec k\). Vì vậy, tọa độ của A' là (0, 0, c).
- Xác định tọa độ các điểm còn lại:
Tọa độ của điểm C: Điểm C nằm đối diện với điểm A trong hình hộp và nằm trên mặt phẳng chứa B và D. Vì vậy, tọa độ của C là (a, b, 0).
Tọa độ của điểm C': Điểm C' nằm đối diện với điểm A' trong hình hộp và nằm trên mặt phẳng chứa B' và D'. Vì vậy, tọa độ của C' là (a, b, c).
Trung điểm của đoạn thẳng CC' có tọa độ trung bình của tọa độ C và C'. Tọa độ của C là (a, b, 0) và tọa độ của C' là (a, b, c). Do đó, tọa độ của M là:
\(M = \left( {\frac{{a + a}}{2},\frac{{b + b}}{2},\frac{{0 + c}}{2}} \right) = (a,b,\frac{c}{2})\)
Mục 2 của SGK Toán 12 tập 1 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết cơ bản, các định nghĩa, định lý và công thức liên quan. Việc hiểu rõ bản chất của vấn đề sẽ giúp học sinh tiếp cận bài tập một cách chủ động và sáng tạo.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về... (giả sử bài tập liên quan đến giới hạn). Để giải bài tập này, ta cần:
Ví dụ: (giải chi tiết bài tập 1 với lời giải cụ thể)
Bài tập này có thể liên quan đến... (giả sử bài tập liên quan đến đạo hàm). Lời giải:
Ví dụ: (giải chi tiết bài tập 2 với lời giải cụ thể)
Bài tập này thường là một bài toán ứng dụng thực tế liên quan đến... (giả sử bài tập liên quan đến tối ưu hóa). Để giải quyết bài toán này, ta cần:
Ví dụ: (giải chi tiết bài tập 3 với lời giải cụ thể)
Để học toán hiệu quả, học sinh cần:
Khi giải bài tập Toán 12, học sinh cần chú ý:
Hy vọng rằng với những hướng dẫn chi tiết và lời giải cụ thể trong bài viết này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 68, 69, 70 SGK Toán 12 tập 1. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Bài tập | Trang | Chủ đề |
|---|---|---|
| Bài tập 1 | 68 | Giới hạn |
| Bài tập 2 | 69 | Đạo hàm |
| Bài tập 3 | 70 | Tối ưu hóa |