Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Trong bài viết này, chúng ta sẽ cùng nhau Giải mục 4 trang 30 SGK Toán 12 tập 1, giúp bạn hiểu rõ hơn về kiến thức và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn cam kết mang đến cho bạn những bài giải chính xác, logic và đầy đủ, giúp bạn tự tin hơn trong quá trình học tập.
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau đây: a) (y = frac{{ - {x^2} - 2x - 2}}{{x + 1}}) b) ({rm{y}} = frac{{{x^2} - 2x - 3}}{{x - 2}})
Trả lời câu hỏi Luyện tập 3 trang 30 SGK Toán 12 Cùng khám phá
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau đây:
a) \(y = \frac{{ - {x^2} - 2x - 2}}{{x + 1}}\)
b) \({\rm{y}} = \frac{{{x^2} - 2x - 3}}{{x - 2}}\)
Phương pháp giải:
- Tìm tập xác định của hàm số.
- Xét sự biến thiên của hàm số.
- Vẽ đồ thị hàm số.
Lời giải chi tiết:
a)
- Tập xác định: D = R \ {-1}.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left( {\frac{{ - {{(x + 1)}^2} - 1}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left[ { - (x + 1) - \frac{1}{{x + 1}}} \right] = - \infty .\)
\(\mathop {\lim }\limits_{x \to - {1^ - }} y = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {\frac{{ - {{(x + 1)}^2} - 1}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \left[ { - (x + 1) - \frac{1}{{x + 1}}} \right] = \infty .\)
Suy ra x = -1 là tiệm cận đứng của hàm số.
\(\mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to \infty } [ - (x + 1)] - 0 = - \infty \).
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - \infty } [ - (x + 1)] - 0 = \infty \).
Suy ra hàm số không có tiệm cận ngang
\(\frac{{ - {x^2} - 2x - 2}}{{x + 1}} = - x - 1 + \frac{{ - 1}}{{x + 1}}\) (Sử dụng phép chia đa thức)
Khi \(x \to \pm \infty ,\frac{{ - 1}}{{x + 1}} \to 0\) nên \(y = - x - 1\) là tiệm cận xiên của hàm số.
Ta có: \({y^\prime } = \frac{{ - (2x + 2)(x + 1) + \left( {{x^2} + 2x + 2} \right)}}{{{{(x + 1)}^2}}} = \frac{{ - {x^2} - 2x}}{{{{(x + 1)}^2}}}\).
\({y^\prime } = 0 \leftrightarrow - {x^2} - 2x \leftrightarrow - x(x + 2) = 0 \leftrightarrow x = 0,{\rm{ }}x = - 2\).
Bảng biến thiên:
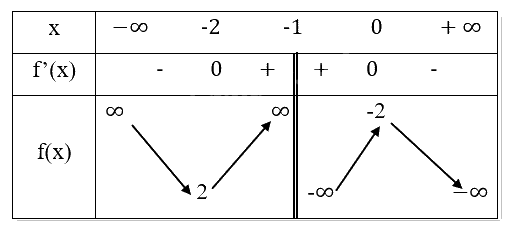
Chiều biến thiên: Hàm số nghịch biến trên các khoảng (−∞,-2) và (-1,0), đồng biến trên khoảng (-2,-1) và (-1,0).
Cực trị: Hàm số đạt cực tiểu tại \(x = - 2,{y_{CT}} = 2\).
Hàm số đạt cực đại tại \(x = 0,{y_{CD}} = - 2\).
- Vẽ đồ thị:
Tiệm cận đứng \({\rm{x}} = - 1\), tiệm cận xiên \(y = - x - 1\).
Giao điểm với trục Oy là \((0, - 2)\).
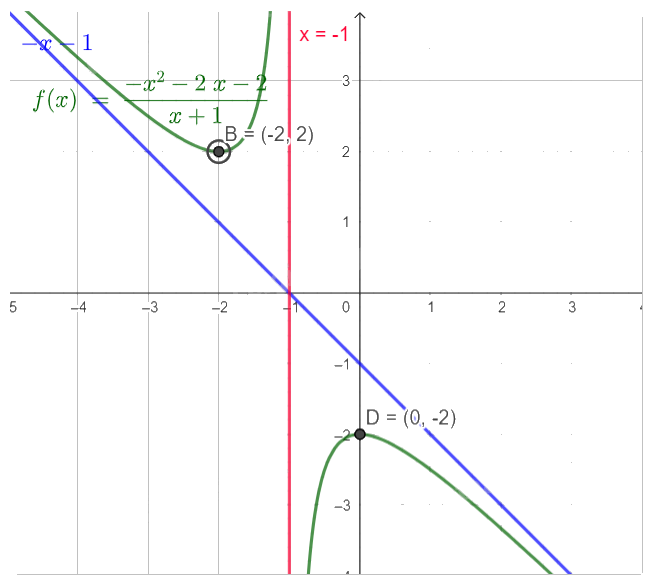
b)
- Tập xác định: D = R \ {2}.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to 2 + } y = \mathop {\lim }\limits_{x \to 2 + } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = - \infty \).
\(\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = \infty \).
Suy ra x = 2 là tiệm cận đứng của hàm số.
\(\mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = \infty \).
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = - \infty \).
Suy ra hàm số không có tiệm cận ngang
\(\frac{{{x^2} - 2x - 3}}{{x - 2}} = x + \frac{{ - 3}}{{x + 1}}\) .
Khi \(x \to \pm \infty ,\frac{{ - 3}}{{x + 1}} \to 0\) nên \(y = x\) là tiệm cận xiên của hàm số.
Ta có: \({y^\prime } = \frac{{(2x - 2)(x - 2) - \left( {{x^2} - 2x - 3} \right)}}{{{{(x - 2)}^2}}} = \frac{{{x^2} - 4x + 7}}{{{{(x - 2)}^2}}} > 0\forall x \in D\).
Vậy hàm số đồng biến trên tập xác định.
Bảng biến thiên:
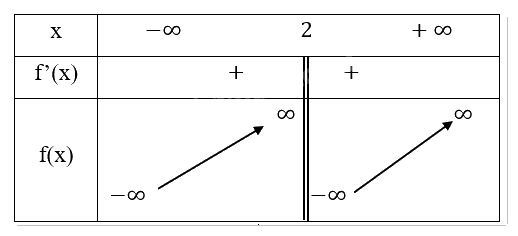
Chiều biến thiên: Hàm số đồng biến trên khoảng (-\(\infty ,2\)) và (2,\(\infty \)).
Cực trị: Hàm số không có cực trị.
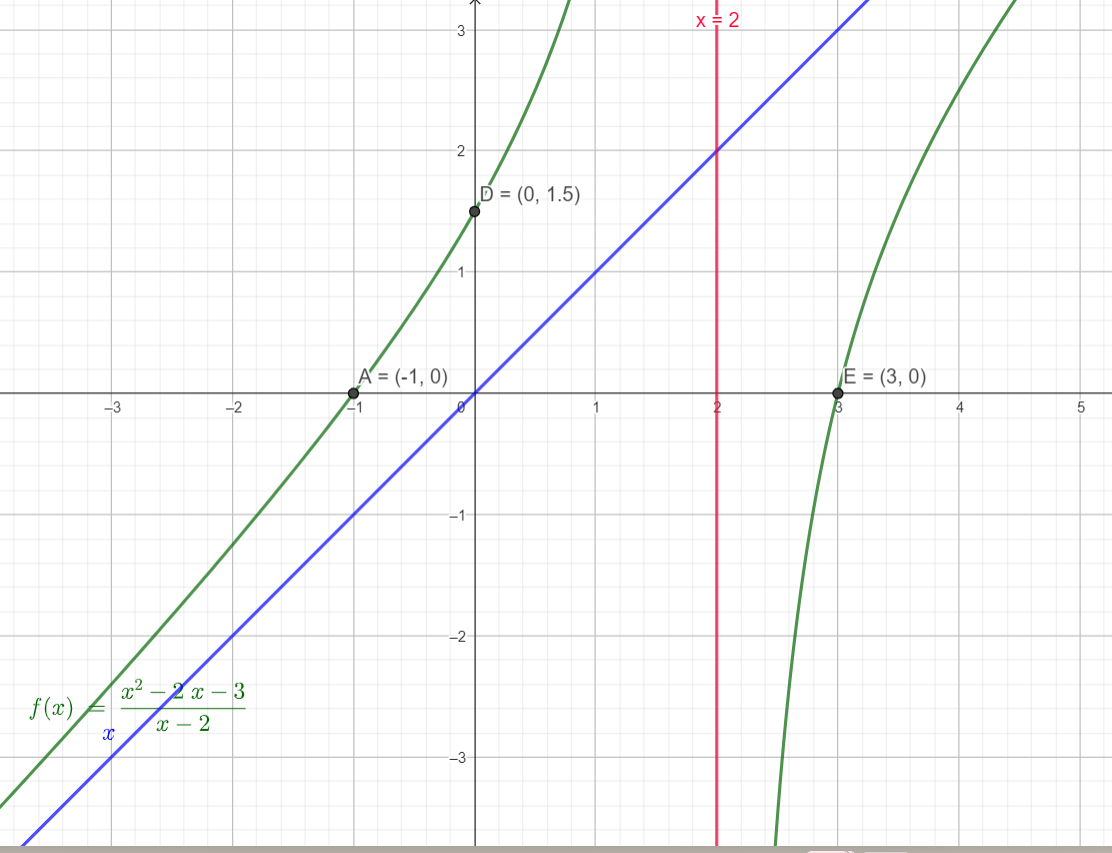
- Vẽ đồ thị:
Tiệm cận đứng x = 2, tiệm cận xiên y = x.
Giao điểm với trục Oy là (0,\(\frac{3}{2}\)).
Giao điểm với trục Ox là (-1,0) và (3,0).
Trả lời câu hỏi Luyện tập 3 trang 30 SGK Toán 12 Cùng khám phá
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau đây:
a) \(y = \frac{{ - {x^2} - 2x - 2}}{{x + 1}}\)
b) \({\rm{y}} = \frac{{{x^2} - 2x - 3}}{{x - 2}}\)
Phương pháp giải:
- Tìm tập xác định của hàm số.
- Xét sự biến thiên của hàm số.
- Vẽ đồ thị hàm số.
Lời giải chi tiết:
a)
- Tập xác định: D = R \ {-1}.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left( {\frac{{ - {{(x + 1)}^2} - 1}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left[ { - (x + 1) - \frac{1}{{x + 1}}} \right] = - \infty .\)
\(\mathop {\lim }\limits_{x \to - {1^ - }} y = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {\frac{{ - {{(x + 1)}^2} - 1}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \left[ { - (x + 1) - \frac{1}{{x + 1}}} \right] = \infty .\)
Suy ra x = -1 là tiệm cận đứng của hàm số.
\(\mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to \infty } [ - (x + 1)] - 0 = - \infty \).
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - \infty } [ - (x + 1)] - 0 = \infty \).
Suy ra hàm số không có tiệm cận ngang
\(\frac{{ - {x^2} - 2x - 2}}{{x + 1}} = - x - 1 + \frac{{ - 1}}{{x + 1}}\) (Sử dụng phép chia đa thức)
Khi \(x \to \pm \infty ,\frac{{ - 1}}{{x + 1}} \to 0\) nên \(y = - x - 1\) là tiệm cận xiên của hàm số.
Ta có: \({y^\prime } = \frac{{ - (2x + 2)(x + 1) + \left( {{x^2} + 2x + 2} \right)}}{{{{(x + 1)}^2}}} = \frac{{ - {x^2} - 2x}}{{{{(x + 1)}^2}}}\).
\({y^\prime } = 0 \leftrightarrow - {x^2} - 2x \leftrightarrow - x(x + 2) = 0 \leftrightarrow x = 0,{\rm{ }}x = - 2\).
Bảng biến thiên:
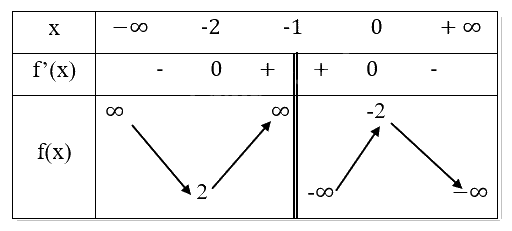
Chiều biến thiên: Hàm số nghịch biến trên các khoảng (−∞,-2) và (-1,0), đồng biến trên khoảng (-2,-1) và (-1,0).
Cực trị: Hàm số đạt cực tiểu tại \(x = - 2,{y_{CT}} = 2\).
Hàm số đạt cực đại tại \(x = 0,{y_{CD}} = - 2\).
- Vẽ đồ thị:
Tiệm cận đứng \({\rm{x}} = - 1\), tiệm cận xiên \(y = - x - 1\).
Giao điểm với trục Oy là \((0, - 2)\).
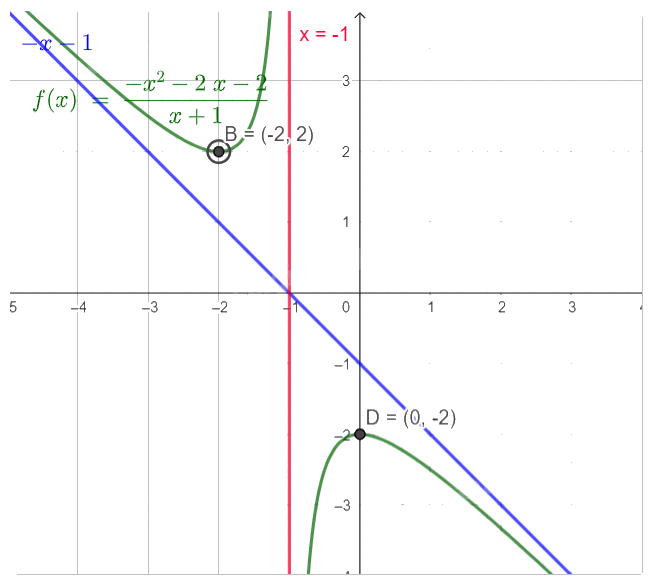
b)
- Tập xác định: D = R \ {2}.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to 2 + } y = \mathop {\lim }\limits_{x \to 2 + } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = - \infty \).
\(\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = \infty \).
Suy ra x = 2 là tiệm cận đứng của hàm số.
\(\mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = \infty \).
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = - \infty \).
Suy ra hàm số không có tiệm cận ngang
\(\frac{{{x^2} - 2x - 3}}{{x - 2}} = x + \frac{{ - 3}}{{x + 1}}\) .
Khi \(x \to \pm \infty ,\frac{{ - 3}}{{x + 1}} \to 0\) nên \(y = x\) là tiệm cận xiên của hàm số.
Ta có: \({y^\prime } = \frac{{(2x - 2)(x - 2) - \left( {{x^2} - 2x - 3} \right)}}{{{{(x - 2)}^2}}} = \frac{{{x^2} - 4x + 7}}{{{{(x - 2)}^2}}} > 0\forall x \in D\).
Vậy hàm số đồng biến trên tập xác định.
Bảng biến thiên:
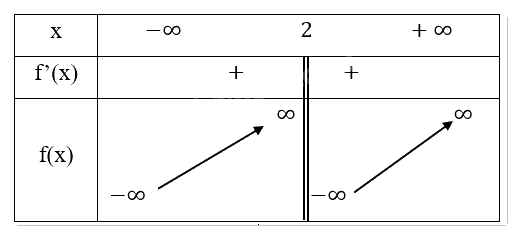
Chiều biến thiên: Hàm số đồng biến trên khoảng (-\(\infty ,2\)) và (2,\(\infty \)).
Cực trị: Hàm số không có cực trị.
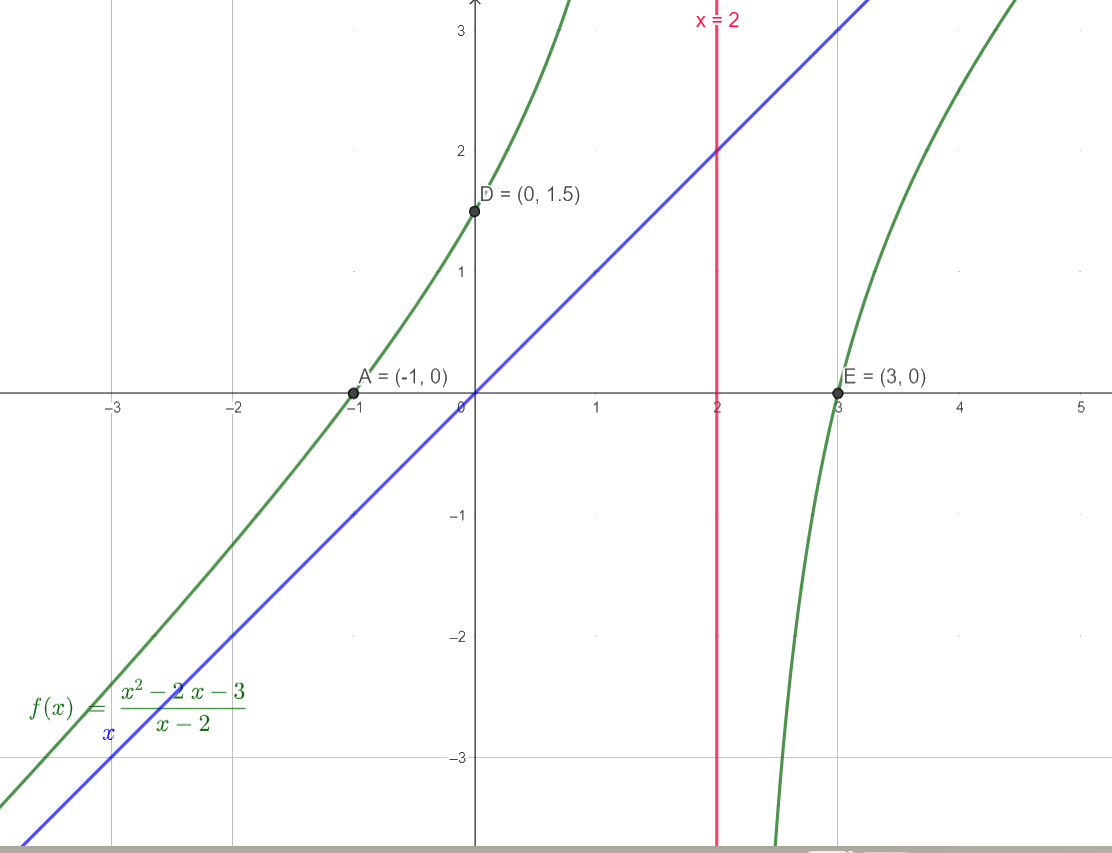
- Vẽ đồ thị:
Tiệm cận đứng x = 2, tiệm cận xiên y = x.
Giao điểm với trục Oy là (0,\(\frac{3}{2}\)).
Giao điểm với trục Ox là (-1,0) và (3,0).
Mục 4 trang 30 SGK Toán 12 tập 1 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các dạng bài tập như tính đạo hàm, tìm đạo hàm cấp hai, và ứng dụng đạo hàm để xét tính đơn điệu của hàm số. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 12.
Để giúp các em học sinh hiểu rõ hơn về cách giải các bài tập trong mục 4 trang 30, chúng ta sẽ đi vào phân tích từng bài tập cụ thể. Dưới đây là lời giải chi tiết cho từng bài tập:
Để tính đạo hàm của hàm số f(x) = x^3 - 2x^2 + 5x - 1, ta sử dụng các quy tắc đạo hàm cơ bản:
Áp dụng các quy tắc trên, ta có:
f'(x) = 3x^2 - 4x + 5
Để tìm đạo hàm cấp hai của hàm số g(x) = sin(2x), ta thực hiện các bước sau:
Để xét tính đơn điệu của hàm số h(x) = x^2 - 4x + 3, ta thực hiện các bước sau:
Ngoài các bài tập đã trình bày ở trên, mục 4 trang 30 SGK Toán 12 tập 1 còn xuất hiện nhiều dạng bài tập khác, như:
Để giải các bài tập về đạo hàm một cách hiệu quả, bạn nên:
Hy vọng rằng với những hướng dẫn chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 4 trang 30 SGK Toán 12 tập 1. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | f'(x) = 3x^2 - 4x + 5 |
| Bài 2 | g''(x) = -4sin(2x) |
| Bài 3 | Hàm số nghịch biến trên (-∞, 2) và đồng biến trên (2, +∞) |