Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 của chương trình học, cụ thể là trang 10, 11 và 12 của sách giáo khoa Toán 12 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của từng bài toán, nắm vững phương pháp giải và tự tin làm bài tập. Hãy cùng bắt đầu nhé!
Định nghĩa
Trả lời câu hỏi Luyện tập 1 trang 11 SGK Toán 12 Cùng khám phá
Tìm giá trị lớn nhất, giá trị bé nhất của hàm số\(y = f(x) = {x^3} - 6{x^2} + 9x + 1\) trên nửa khoảng\([ - 1;4)\)
Phương pháp giải:
Bước 1: Tính\(f'(x)\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định giá trị lớn nhất, giá trị bé nhất của hàm số trên nửa khoảng \([ - 1;4)\)
Lời giải chi tiết:
Ta có: \(f'(x) = 3{x^2} - 12x + 9\)
Xét \(f'(x) = 0\)
\( \Rightarrow 3{x^2} - 12x + 9 = 0\)
\( \Rightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Ta có bảng biến thiên là
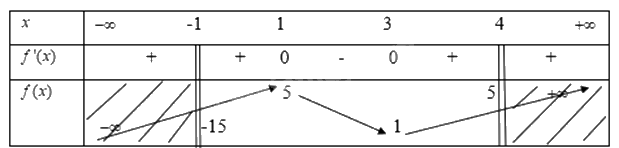
Từ bảng biến thiên ta thấy
Hàm số đạt giá trị cực đại trong nửa khoảng \([ - 1;4)\) tại \(x = 1\) khi đó \(y = 5\)
Và đạt giá trị cực tiểu trong nửa khoảng \([ - 1;4)\) tại\(x = - 1\) khi đó \(y = - 15\)
Trả lời câu hỏi Hoạt động 1 trang 10 SGK Toán 12 Cùng khám phá
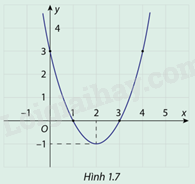
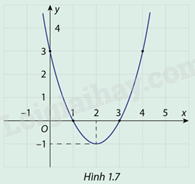
Cho hàm số \(y = f(x) = {x^2} - 4x + 3\) có đồ thị như hình 1.7
a) Tìm tọa độ điểm thấp nhất của đồ thị hàm số \(f(x)\) đã cho
b) Khi \(x\)thay đổi trên đoạn \([1;4]\), tìm \({x_0} \in [1;4]\) để \(f({x_0})\)có giá trị lớn nhất
Phương pháp giải:
a) Nhìn đồ thị hàm số rồi rút ra điểm có tọa dộ thấp nhất
b) Lập bảng biến thiên rồi tìm \({x_0} \in [1;4]\) để \(f({x_0})\) lớn nhất
Lời giải chi tiết:
a) Dựa vào dồ thị hàm số ta thấy tọa độ điểm thấp nhất là (2;-1)
b) Ta có: \(y' = 2x - 4\)
Xét \(y' = 0\)\( \Rightarrow 2x - 4 = 0\) \( \Rightarrow x = 2\)
Ta có bảng biến thiên
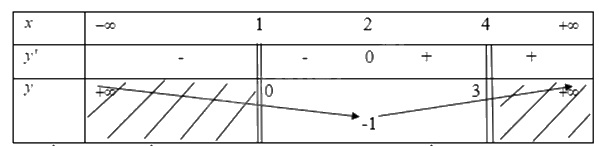
Từ bảng biến thiên ta thấy tại \({x_0} = 4\) thì \(f({x_0})\) đạt giá trị lớn nhất
Trả lời câu hỏi Luyện tập 2 trang 12 SGK Toán 12 Cùng khám phá
Trong một trò chơi, mỗi đội được phát một tấm bìa hình vuông có cạnh bằng 30 cm. Nhiệm vụ của mỗi đội chơi là cắt ở 4 góc của tấm bìa này 4 hình vuông bằng nhau rồi gập tấm bìa lại( hình 1.6) và dán keo để được một cái hộp không nắp có dạng hình hộp chữ nhật. Đội nào thiết kế được cái hộp có thể tích lớn nhất sẽ dành chiến thắng. Hãy xác định cạnh của các hình vuông bị cắt để thu được hộp có thể tích lớn nhất.
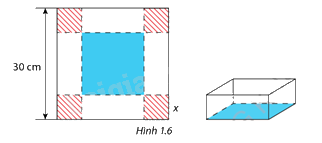
Phương pháp giải:
Bước 1: Lập công thức tính thể tích hình hộp dước dạng hàm số
Bước 2: Lập bảng biến thiên của hàm số
Bước 3: Tính thể tích lớn nhất của hình hộp là tìm giá trị lớn nhât của hàm số
Lời giải chi tiết:
Gọi độ dài hình vuông cần cắt là \(x(cm,0 < x < 30)\)
Khi đó độ dài cạnh hình hộp là\(30 - 2x\)(>0)
Thể tích hình hộp là
\(V = x(30 - 2x)(30 - 2x)\)
\( = 4{x^3} - 120{x^2} + 900x\)
Ta có \(V' = 12{x^2} - 240x + 900\)
Xét \(V' = 0\)
\( \Rightarrow 12{x^2} - 240x + 900 = 0\)
\( \Rightarrow \left[ \begin{array}{l}x = 5\\x = 15\end{array} \right.\)
Ta có bảng biến thiên
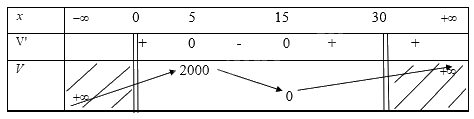
Từ bảng biến thiên ta thấy với \(x = 5\) thì thể tích hình hộp đạt giá trị lớn nhất là 2000
Trả lời câu hỏi Hoạt động 1 trang 10 SGK Toán 12 Cùng khám phá
Cho hàm số \(y = f(x) = {x^2} - 4x + 3\) có đồ thị như hình 1.7
a) Tìm tọa độ điểm thấp nhất của đồ thị hàm số \(f(x)\) đã cho
b) Khi \(x\)thay đổi trên đoạn \([1;4]\), tìm \({x_0} \in [1;4]\) để \(f({x_0})\)có giá trị lớn nhất
Phương pháp giải:
a) Nhìn đồ thị hàm số rồi rút ra điểm có tọa dộ thấp nhất
b) Lập bảng biến thiên rồi tìm \({x_0} \in [1;4]\) để \(f({x_0})\) lớn nhất
Lời giải chi tiết:
a) Dựa vào dồ thị hàm số ta thấy tọa độ điểm thấp nhất là (2;-1)
b) Ta có: \(y' = 2x - 4\)
Xét \(y' = 0\)\( \Rightarrow 2x - 4 = 0\) \( \Rightarrow x = 2\)
Ta có bảng biến thiên
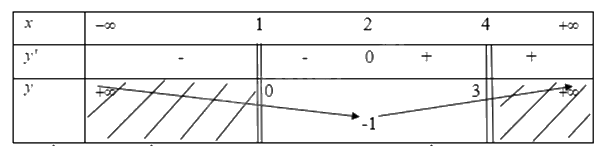
Từ bảng biến thiên ta thấy tại \({x_0} = 4\) thì \(f({x_0})\) đạt giá trị lớn nhất
Trả lời câu hỏi Luyện tập 1 trang 11 SGK Toán 12 Cùng khám phá
Tìm giá trị lớn nhất, giá trị bé nhất của hàm số\(y = f(x) = {x^3} - 6{x^2} + 9x + 1\) trên nửa khoảng\([ - 1;4)\)
Phương pháp giải:
Bước 1: Tính\(f'(x)\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định giá trị lớn nhất, giá trị bé nhất của hàm số trên nửa khoảng \([ - 1;4)\)
Lời giải chi tiết:
Ta có: \(f'(x) = 3{x^2} - 12x + 9\)
Xét \(f'(x) = 0\)
\( \Rightarrow 3{x^2} - 12x + 9 = 0\)
\( \Rightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Ta có bảng biến thiên là
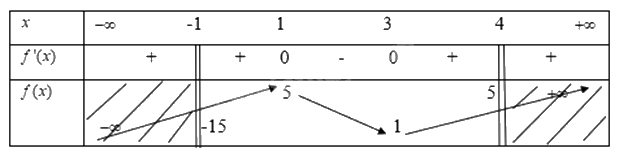
Từ bảng biến thiên ta thấy
Hàm số đạt giá trị cực đại trong nửa khoảng \([ - 1;4)\) tại \(x = 1\) khi đó \(y = 5\)
Và đạt giá trị cực tiểu trong nửa khoảng \([ - 1;4)\) tại\(x = - 1\) khi đó \(y = - 15\)
Trả lời câu hỏi Luyện tập 2 trang 12 SGK Toán 12 Cùng khám phá
Trong một trò chơi, mỗi đội được phát một tấm bìa hình vuông có cạnh bằng 30 cm. Nhiệm vụ của mỗi đội chơi là cắt ở 4 góc của tấm bìa này 4 hình vuông bằng nhau rồi gập tấm bìa lại( hình 1.6) và dán keo để được một cái hộp không nắp có dạng hình hộp chữ nhật. Đội nào thiết kế được cái hộp có thể tích lớn nhất sẽ dành chiến thắng. Hãy xác định cạnh của các hình vuông bị cắt để thu được hộp có thể tích lớn nhất.
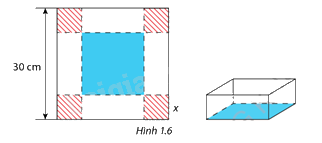
Phương pháp giải:
Bước 1: Lập công thức tính thể tích hình hộp dước dạng hàm số
Bước 2: Lập bảng biến thiên của hàm số
Bước 3: Tính thể tích lớn nhất của hình hộp là tìm giá trị lớn nhât của hàm số
Lời giải chi tiết:
Gọi độ dài hình vuông cần cắt là \(x(cm,0 < x < 30)\)
Khi đó độ dài cạnh hình hộp là\(30 - 2x\)(>0)
Thể tích hình hộp là
\(V = x(30 - 2x)(30 - 2x)\)
\( = 4{x^3} - 120{x^2} + 900x\)
Ta có \(V' = 12{x^2} - 240x + 900\)
Xét \(V' = 0\)
\( \Rightarrow 12{x^2} - 240x + 900 = 0\)
\( \Rightarrow \left[ \begin{array}{l}x = 5\\x = 15\end{array} \right.\)
Ta có bảng biến thiên
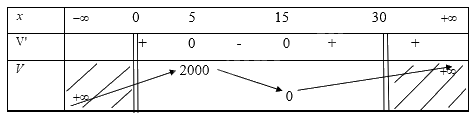
Từ bảng biến thiên ta thấy với \(x = 5\) thì thể tích hình hộp đạt giá trị lớn nhất là 2000
Mục 1 của SGK Toán 12 tập 1 thường tập trung vào các kiến thức nền tảng về hàm số, bao gồm các loại hàm số cơ bản như hàm số bậc nhất, hàm số bậc hai, hàm số mũ, hàm số logarit và các phép biến đổi hàm số. Việc nắm vững kiến thức này là vô cùng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Trang 10 thường chứa các bài tập về hàm số bậc nhất và hàm số bậc hai. Các bài tập này thường yêu cầu học sinh xác định các yếu tố của hàm số (hệ số a, b, c), vẽ đồ thị hàm số, tìm tập xác định, tập giá trị, khoảng đồng biến, nghịch biến và giải các phương trình, bất phương trình liên quan đến hàm số.
Trang 11 thường chứa các bài tập về hàm số bậc hai. Các bài tập này thường yêu cầu học sinh xác định các yếu tố của hàm số (hệ số a, b, c), tìm đỉnh của parabol, trục đối xứng, khoảng đồng biến, nghịch biến và giải các phương trình, bất phương trình liên quan đến hàm số.
Trang 12 thường chứa các bài tập tổng hợp về hàm số bậc nhất và hàm số bậc hai, cũng như các bài tập ứng dụng thực tế. Các bài tập này thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề phức tạp hơn.
| Bài tập | Nội dung |
|---|---|
| Bài 7 | Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. |
| Bài 8 | Giải bài toán thực tế liên quan đến hàm số. |
| Bài 9 | Khảo sát hàm số và vẽ đồ thị. |
Để giải tốt các bài tập về hàm số, học sinh cần nắm vững các kiến thức cơ bản về hàm số, các phép biến đổi hàm số và các phương pháp giải phương trình, bất phương trình. Ngoài ra, việc luyện tập thường xuyên và làm quen với các dạng bài tập khác nhau cũng rất quan trọng.
Một số phương pháp giải bài tập hàm số thường được sử dụng:
Để học tốt môn Toán nói chung và các bài tập về hàm số nói riêng, các em cần:
Hy vọng rằng với bài viết này, các em học sinh đã có thể hiểu rõ hơn về cách giải các bài tập trong mục 1 trang 10, 11, 12 SGK Toán 12 tập 1. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!