Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 3 trang 19, 20, 21 của sách giáo khoa Toán 12 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải và tự tin làm bài tập.
Trong Hình 1.21, đường cong là đồ thị ( C ) của hàm số (y = f(x) = x + frac{x}{{{x^2} - 1}}) và đường thẳng (Delta :y = x) . Gọi M, N lần lượt là hai điểm thuộc ( C ) và(Delta ) có cùng hoành độ x, với x > 1 hoặc x < -1. Nhận xét về độ dài của đoạn MN khi(x to - infty ) và (x to + infty )
Trả lời câu hỏi Luyện tập 3 trang 20 SGK Toán 12 Cùng khám phá
Sử dụng ghi chú ở trên, tìm tiệm cận xiên của đồ thị hàm số \(y = f(x) = \frac{{ - {x^2} - 3x - 3}}{{x + 1}}\).
Phương pháp giải:
Phân tích hàm số rồi áp dụng ghi chú: hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (\(a \ne 0,m \ne 0\) đa thức tử không chia hết cho đa thức mẫu) luôn được viết dưới dạng \(y = px + q + \frac{r}{{mx + n}}\)\((p,q,r \in R)\).Khi đó đồ thị hàm số có đường tiệm cận đứng \(x = - \frac{n}{m}\)là và đường tiệm cận xiên là \(y = px + q.\)
Lời giải chi tiết:
Ta có \(y = f(x) = \frac{{ - {x^2} - 3x - 3}}{{x + 1}}\)\( = - x - 2 - \frac{1}{{x + 1}}.\)
Áp dụng ghi chú hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (\(a \ne 0,m \ne 0\) đa thức tử không chia hết cho đa thức mẫu) luôn được viết dưới dạng \(y = px + q + \frac{r}{{mx + n}}\)\((p,q,r \in R)\).Khi đó đồ thị hàm số có đường tiệm cận xiên là \(y = px + q\), khi đó đường tiệm cận xiên của hàm số là \(y = - x - 2.\)
Trả lời câu hỏi Vận dụng 1 trang 20 SGK Toán 12 Cùng khám phá
Trong phần Khởi động đầu bài, tìm đường tiệm cận đứng của đồ thị hàm số \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\), từ đó nhận xét khối lượng của vật khi vận tốc của nó càng gần vận tốc ánh sáng.
Phương pháp giải:
Tìm giới hạn của khối lượng m(v) khi vận tốc v tiến gần đến tốc độ ánh sáng c.
Lời giải chi tiết:
Xét \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\).
Tập xác định: \(D = \mathbb{N}\backslash \{ c\} \).
Ta có: \(\mathop {\lim }\limits_{v \to {c^ + }} m(v) = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = + \infty .\)
\(\mathop {\lim }\limits_{v \to c - } m(v) = \mathop {\lim }\limits_{v \to {c^ - }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to c - } \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = + \infty .\)
Vậy đường thẳng x = c là tiệm cận đứng của đồ thị hàm số. Khi vận tốc của vật tiến dần đến tốc độ ánh sáng, khối lượng của vật càng lớn.
Trả lời câu hỏi Hoạt động 3 trang 19 SGK Toán 12 Cùng khám phá
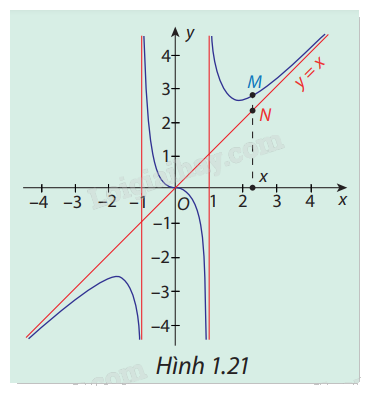
Trong Hình 1.21, đường cong là đồ thị ( C ) của hàm số \(y = f(x) = x + \frac{x}{{{x^2} - 1}}\) và đường thẳng \(\Delta :y = x\) . Gọi M, N lần lượt là hai điểm thuộc ( C ) và\(\Delta \) có cùng hoành độ x, với x > 1 hoặc x < -1. Nhận xét về độ dài của đoạn MN khi\(x \to - \infty \) và \(x \to + \infty .\)
Phương pháp giải:
Nhìn vào đồ thị rồi nhận xét.
Lời giải chi tiết:
Khi \(x \to - \infty \) và \(x \to + \infty \) thì độ dài MN càng ngắn.
Trả lời câu hỏi Vận dụng 2 trang 21 SGK Toán 12 Cùng khám phá
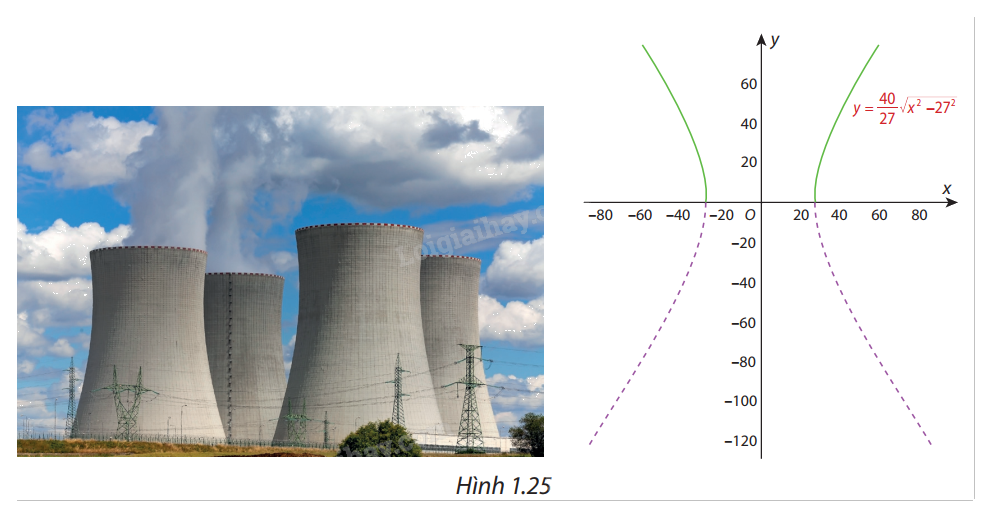
Một ống khói của nhà máy điện hạt nhân có mặt cắt là một hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) (Hình 1.25). Hét hai nhánh bên trên Ox của (H) là đồ thị (C) của hàm số \(y = \frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} \) (phần nét liền đậm). Chứng minh rằng đường thẳng \(y = \frac{{40}}{{27}}x\) là một đường tiệm cận của (C). Hãy chỉ ra them một đường tiệm cận xiên khác của (C).
Phương pháp giải:
Chứng minh \(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} - \frac{{40}}{{27}}x} \right) = 0\).
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} - \frac{{40}}{{27}}x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{40}}{{27}}\left( {\sqrt {{x^2} - {{27}^2}} - x} \right)} \right] = \frac{{40}}{{27}}\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - {{27}^2}} - x} \right)\)
\( = \frac{{40}}{{27}}\mathop {\lim }\limits_{x \to + \infty } \frac{{40}}{{27}}.\frac{{{x^2} - {{27}^2} - {x^2}}}{{\sqrt {{x^2} - {{27}^2}} + x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{40}}{{27}}.\left( {\frac{{ - {{27}^2}}}{{\sqrt {{x^2} - {{27}^2}} + x}}} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 40.27}}{{\sqrt {{x^2} - {{27}^2}} + x}}\)
\( = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 40.27}}{{x\sqrt {1 - \frac{{{{27}^2}}}{{{x^2}}}} + x}} = 0.\)
Vậy \(y = \frac{{40}}{{27}}x\) là tiệm cận xiên của (C).
Tương tự, một tiệm cận xiên khác của (C) là \(y = - \frac{{40}}{{27}}x\).
Trả lời câu hỏi Hoạt động 3 trang 19 SGK Toán 12 Cùng khám phá
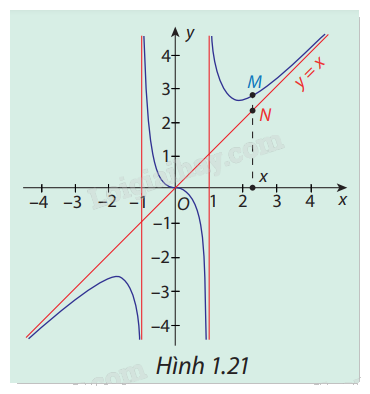
Trong Hình 1.21, đường cong là đồ thị ( C ) của hàm số \(y = f(x) = x + \frac{x}{{{x^2} - 1}}\) và đường thẳng \(\Delta :y = x\) . Gọi M, N lần lượt là hai điểm thuộc ( C ) và\(\Delta \) có cùng hoành độ x, với x > 1 hoặc x < -1. Nhận xét về độ dài của đoạn MN khi\(x \to - \infty \) và \(x \to + \infty .\)
Phương pháp giải:
Nhìn vào đồ thị rồi nhận xét.
Lời giải chi tiết:
Khi \(x \to - \infty \) và \(x \to + \infty \) thì độ dài MN càng ngắn.
Trả lời câu hỏi Luyện tập 3 trang 20 SGK Toán 12 Cùng khám phá
Sử dụng ghi chú ở trên, tìm tiệm cận xiên của đồ thị hàm số \(y = f(x) = \frac{{ - {x^2} - 3x - 3}}{{x + 1}}\).
Phương pháp giải:
Phân tích hàm số rồi áp dụng ghi chú: hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (\(a \ne 0,m \ne 0\) đa thức tử không chia hết cho đa thức mẫu) luôn được viết dưới dạng \(y = px + q + \frac{r}{{mx + n}}\)\((p,q,r \in R)\).Khi đó đồ thị hàm số có đường tiệm cận đứng \(x = - \frac{n}{m}\)là và đường tiệm cận xiên là \(y = px + q.\)
Lời giải chi tiết:
Ta có \(y = f(x) = \frac{{ - {x^2} - 3x - 3}}{{x + 1}}\)\( = - x - 2 - \frac{1}{{x + 1}}.\)
Áp dụng ghi chú hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (\(a \ne 0,m \ne 0\) đa thức tử không chia hết cho đa thức mẫu) luôn được viết dưới dạng \(y = px + q + \frac{r}{{mx + n}}\)\((p,q,r \in R)\).Khi đó đồ thị hàm số có đường tiệm cận xiên là \(y = px + q\), khi đó đường tiệm cận xiên của hàm số là \(y = - x - 2.\)
Trả lời câu hỏi Vận dụng 1 trang 20 SGK Toán 12 Cùng khám phá
Trong phần Khởi động đầu bài, tìm đường tiệm cận đứng của đồ thị hàm số \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\), từ đó nhận xét khối lượng của vật khi vận tốc của nó càng gần vận tốc ánh sáng.
Phương pháp giải:
Tìm giới hạn của khối lượng m(v) khi vận tốc v tiến gần đến tốc độ ánh sáng c.
Lời giải chi tiết:
Xét \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\).
Tập xác định: \(D = \mathbb{N}\backslash \{ c\} \).
Ta có: \(\mathop {\lim }\limits_{v \to {c^ + }} m(v) = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = + \infty .\)
\(\mathop {\lim }\limits_{v \to c - } m(v) = \mathop {\lim }\limits_{v \to {c^ - }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to c - } \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = + \infty .\)
Vậy đường thẳng x = c là tiệm cận đứng của đồ thị hàm số. Khi vận tốc của vật tiến dần đến tốc độ ánh sáng, khối lượng của vật càng lớn.
Trả lời câu hỏi Vận dụng 2 trang 21 SGK Toán 12 Cùng khám phá
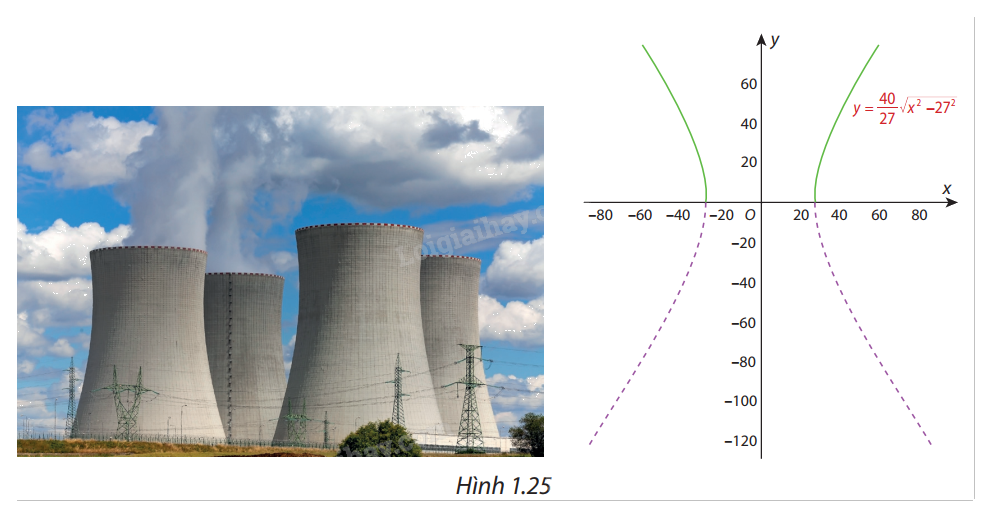
Một ống khói của nhà máy điện hạt nhân có mặt cắt là một hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) (Hình 1.25). Hét hai nhánh bên trên Ox của (H) là đồ thị (C) của hàm số \(y = \frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} \) (phần nét liền đậm). Chứng minh rằng đường thẳng \(y = \frac{{40}}{{27}}x\) là một đường tiệm cận của (C). Hãy chỉ ra them một đường tiệm cận xiên khác của (C).
Phương pháp giải:
Chứng minh \(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} - \frac{{40}}{{27}}x} \right) = 0\).
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} - \frac{{40}}{{27}}x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{40}}{{27}}\left( {\sqrt {{x^2} - {{27}^2}} - x} \right)} \right] = \frac{{40}}{{27}}\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - {{27}^2}} - x} \right)\)
\( = \frac{{40}}{{27}}\mathop {\lim }\limits_{x \to + \infty } \frac{{40}}{{27}}.\frac{{{x^2} - {{27}^2} - {x^2}}}{{\sqrt {{x^2} - {{27}^2}} + x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{40}}{{27}}.\left( {\frac{{ - {{27}^2}}}{{\sqrt {{x^2} - {{27}^2}} + x}}} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 40.27}}{{\sqrt {{x^2} - {{27}^2}} + x}}\)
\( = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 40.27}}{{x\sqrt {1 - \frac{{{{27}^2}}}{{{x^2}}}} + x}} = 0.\)
Vậy \(y = \frac{{40}}{{27}}x\) là tiệm cận xiên của (C).
Tương tự, một tiệm cận xiên khác của (C) là \(y = - \frac{{40}}{{27}}x\).
Mục 3 trong SGK Toán 12 tập 1 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết cơ bản, các định nghĩa, định lý và công thức liên quan. Việc hiểu rõ bản chất của vấn đề sẽ giúp học sinh tiếp cận bài tập một cách chủ động và sáng tạo.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về... (giả sử bài tập liên quan đến giới hạn). Để giải bài tập này, ta cần:
Ví dụ minh họa: ... (giải chi tiết bài tập)
Bài tập này có thể liên quan đến... (giả sử bài tập liên quan đến đạo hàm). Cách giải:
Ví dụ minh họa: ... (giải chi tiết bài tập)
Bài tập này thường là một bài toán ứng dụng thực tế, yêu cầu học sinh kết hợp kiến thức về... (giả sử bài tập liên quan đến tích phân). Để giải quyết bài toán này, ta cần:
Ví dụ minh họa: ... (giải chi tiết bài tập)
Để học toán hiệu quả, học sinh cần:
Khi giải bài tập Toán 12, học sinh cần chú ý:
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 3 trang 19, 20, 21 SGK Toán 12 tập 1. Chúc các em học tập tốt và đạt kết quả cao!