Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 69, 70 SGK Toán 12 tập 2 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án và phương pháp giải các bài tập trong mục, giúp các em hiểu rõ kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất để hỗ trợ các em trong quá trình học tập.
Cho hai mặt phẳng \((\alpha )\) và \((\beta )\) lần lượt có các vectơ pháp tuyến là \(\vec n\) và \(\vec n'\). Lấy hai đường thẳng \(a\), \(a'\) cùng vuông góc với \((\alpha )\), và hai đường thẳng \(b\), \(b'\) cùng vuông góc với \((\beta )\). (Hình 5.28) Hỏi hai góc \((a,b)\) và \((a',b')\) có bằng nhau không? Vì sao?
Trả lời câu hỏi Luyện tập 3 trang 70 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tính góc giữa mặt phẳng \((\alpha ):\sqrt 3 x - y + 2 = 0\) và các mặt phẳng toạ độ \((Oxy)\), \((Oxz)\), \((Oyz)\).
Phương pháp giải:
- Xác định vectơ pháp tuyến của mặt phẳng \((\alpha )\).
- Góc giữa hai mặt phẳng là góc giữa các vectơ pháp tuyến của chúng:
\(\cos \theta = \frac{{{{\vec n}_1} \cdot {{\vec n}_2}}}{{|{{\vec n}_1}||{{\vec n}_2}|}}\)
Trong đó, \({\vec n_1} \cdot {\vec n_2}\) là tích vô hướng, \(|{\vec n_1}|\) và \(|{\vec n_2}|\) là độ lớn của các vectơ.
Lời giải chi tiết:
Cho mặt phẳng \((\alpha )\): \(\sqrt 3 x - y + 2 = 0\).
Vectơ pháp tuyến của mặt phẳng \(\alpha \): \({\vec n_\alpha } = (\sqrt 3 , - 1,0)\).
Góc giữa mặt phẳng \((\alpha )\) và Oxy:
- Vectơ pháp tuyến của Oxy: \({\vec n_{Oxy}} = (0,0,1)\).
Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oxy}} = \sqrt 3 .0 + ( - 1).0 + 0.1 = 0\)
Độ lớn:
\(|{\vec n_\alpha }| = \sqrt {3 + 1 + 0} = 2,\quad |{\vec n_{Oxy}}| = \sqrt {0 + 0 + 1} = 1\)
\(\cos \theta = \frac{0}{{2 \times 1}} = 0\quad \Rightarrow \theta = {90^\circ }\)
Góc giữa mặt phẳng \((\alpha )\) và Oxz:
- Vectơ pháp tuyến của Oxz: \({\vec n_{Oxz}} = (0,1,0)\).
Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oxz}} = \sqrt 3 .0 + ( - 1).1 + 0.0 = - 1\)
Độ lớn:
\(|{\vec n_{Oxz}}| = \sqrt {0 + 1 + 0} = 1\)
\(\cos \theta = \frac{{ - 1}}{{2 \times 1}} = - \frac{1}{2}\quad \Rightarrow \theta = {120^\circ }\)
Góc giữa mặt phẳng \((\alpha )\) và Oyz:
- Vectơ pháp tuyến của Oyz: \({\vec n_{Oyz}} = (1,0,0)\). Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oyz}} = \sqrt 3 .1 + ( - 1).0 + 0.0 = \sqrt 3 \)
Độ lớn:
\(|{\vec n_{Oyz}}| = \sqrt {1 + 0 + 0} = 1\)
\(\cos \theta = \frac{{\sqrt 3 }}{{2 \times 1}} = \frac{{\sqrt 3 }}{2}\quad \Rightarrow \theta = {30^\circ }\)
Trả lời câu hỏi Vận dụng trang 70 SGK Toán 12 Cùng khám phá
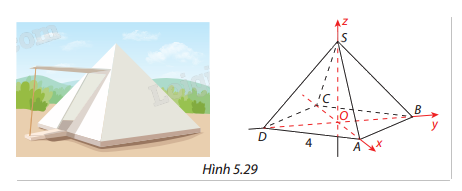
Để chuẩn bị cho chuyến đi dã ngoại, nhóm bạn Đức thiết kế lều cắm trại dạng hình chóp từ giác đều có đáy là hình vuông cạnh 4m. Theo bản vẽ thiết kế thì góc giữa hai mặt bên của lều bằng 60°. Bằng phương pháp tọa độ, hãy tính chiều cao của lều này.
Phương pháp giải:
- Xây dựng hệ tọa độ và xác định tọa độ các điểm
- Xác định vector pháp tuyến của các mặt bên
- Sử dụng công thức tính góc giữa hai mặt phẳng qua vector pháp tuyến
- Giải phương trình để tìm chiều cao
Lời giải chi tiết:
Gọi h là chiều cao cần tìm của hình chóp S.ABCD.
Do mặt đáy là hình vuông cạnh 4m nên \(OA = OB = OC = OD = 2\sqrt 2 \)
Toạ độ các điểm là \(A(2\sqrt 2 ;0;0)\), \(B(0;2\sqrt 2 ;0)\), \(C( - 2\sqrt 2 ;0;0)\), \(D(0; - 2\sqrt 2 ;0)\) và \(S(0;0;h)\).
Vectơ chỉ phương của mặt phẳng SAB là \(\overrightarrow {AB} = ( - 2\sqrt 2 ;2\sqrt 2 ;0)\) và \(\overrightarrow {SA} = (2\sqrt 2 ;0; - h)\)
Suy ra vectơ pháp tuyến của mặt phẳng SAB là
\(\overrightarrow {{n_{SAB}}} = \overrightarrow {AB} .\overrightarrow {SA} = (2\sqrt 2 .( - h) - 0.0;\,\,\,0.2\sqrt 2 - ( - 2\sqrt 2 ).( - h);\,\,\,( - 2\sqrt 2 ).0 - 2\sqrt 2 .2\sqrt 2 = ( - 2\sqrt 2 .h; - 2\sqrt 2 .h; - 8)\)
Vectơ chỉ phương của mặt phẳng SCD là \(\overrightarrow {DC} = ( - 2\sqrt 2 ;2\sqrt 2 ;0)\) và \(\overrightarrow {SC} = ( - 2\sqrt 2 ;0; - h)\)
Suy ra vectơ pháp tuyến của mặt phẳng SCD là
\(\overrightarrow {{n_{SCD}}} = \overrightarrow {DC} .\overrightarrow {SC} = (2\sqrt 2 .( - h) - 0.0;\,\,\,0.( - 2\sqrt 2 ) - ( - 2\sqrt 2 ).( - h);\,\,\,( - 2\sqrt 2 ).0 - 2\sqrt 2 .( - 2\sqrt 2 )) = ( - 2\sqrt 2 .h; - 2\sqrt 2 .h;8)\)
Ta có:
\(\overrightarrow {{n_{SAB}}} .\overrightarrow {{n_{SCD}}} = 8{h^2} + 8{h^2} - 64 = 16{h^2} - 64 = 16({h^2} - 4)\)
\(\left| {\overrightarrow {{n_{SAB}}} } \right| = \sqrt {8{h^2} + 8{h^2} + 64} = \sqrt {16{h^2} + 64} = 4\sqrt {{h^2} + 4} \)
\(\left| {\overrightarrow {{n_{SCD}}} } \right| = \sqrt {8{h^2} + 8{h^2} + 64} = \sqrt {16{h^2} + 64} = 4\sqrt {{h^2} + 4} \)
Góc giữa hai mặt phẳng SAB và SCD bằng 60° nên suy ra:
\(\cos 60^\circ = \frac{{16({h^2} - 4)}}{{4\sqrt {{h^2} + 4} .4\sqrt {{h^2} + 4} }} = \frac{{16({h^2} - 4)}}{{16({h^2} + 4)}} = \frac{{{h^2} - 4}}{{{h^2} + 4}} = \frac{1}{2}\)
\( \Leftrightarrow 2{h^2} - 8 = {h^2} + 4\)
\( \Leftrightarrow {h^2} = 12\)
\( \Leftrightarrow h = \sqrt {12} = 2\sqrt 3 \)
Vậy chiều cao của lều là \(2\sqrt 3 \)m.
Trả lời câu hỏi Hoạt động 3 trang 69 SGK Toán 12 Cùng khám phá
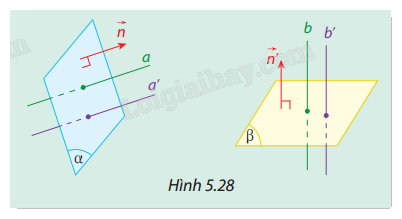
Cho hai mặt phẳng \((\alpha )\) và \((\beta )\) lần lượt có các vectơ pháp tuyến là \(\vec n\) và \(\vec n'\). Lấy hai đường thẳng \(a\), \(a'\) cùng vuông góc với \((\alpha )\), và hai đường thẳng \(b\), \(b'\) cùng vuông góc với \((\beta )\). (Hình 5.28) Hỏi hai góc \((a,b)\) và \((a',b')\) có bằng nhau không? Vì sao?
Phương pháp giải:
Sử dụng tính chất góc giữa hai đường thẳng sẽ bằng góc giữa hai vectơ chỉ phương của chúng.
Lời giải chi tiết:
Vectơ pháp tuyến của mặt phẳng \((\alpha )\) là \(\vec n\), và của mặt phẳng \((\beta )\) là \(\vec n'\).
Nếu hai đường thẳng \(a\) và \(a'\) vuông góc với \((\alpha )\), và \(b\) và \(b'\) vuông góc với \((\beta )\), thì hai vectơ \(\vec n\) và \(\vec n'\)lần lượt là hai vectơ chỉ phương của \(a\) và \(a'\), \(b\) và \(b'\).
Mà góc giữa hai đường thẳng bằng góc giữa hai vectơ chỉ phương của chúng nên
\((a,b) = (a',b')\) do cùng bằng với góc \((\overrightarrow n ,\overrightarrow {n'} )\).
Vậy nếu \(\vec a\) vuông góc với \((\alpha )\) và \(\vec b\) vuông góc với \((\beta )\), thì hai góc \((a,b)\) và \((a',b')\) sẽ bằng nhau vì cùng liên quan đến vectơ pháp tuyến \(\vec n\) và \(\vec n'\).
Trả lời câu hỏi Hoạt động 3 trang 69 SGK Toán 12 Cùng khám phá
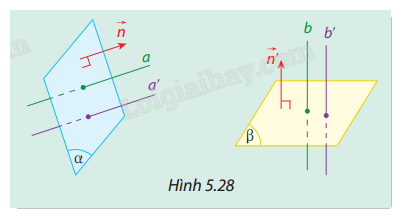
Cho hai mặt phẳng \((\alpha )\) và \((\beta )\) lần lượt có các vectơ pháp tuyến là \(\vec n\) và \(\vec n'\). Lấy hai đường thẳng \(a\), \(a'\) cùng vuông góc với \((\alpha )\), và hai đường thẳng \(b\), \(b'\) cùng vuông góc với \((\beta )\). (Hình 5.28) Hỏi hai góc \((a,b)\) và \((a',b')\) có bằng nhau không? Vì sao?
Phương pháp giải:
Sử dụng tính chất góc giữa hai đường thẳng sẽ bằng góc giữa hai vectơ chỉ phương của chúng.
Lời giải chi tiết:
Vectơ pháp tuyến của mặt phẳng \((\alpha )\) là \(\vec n\), và của mặt phẳng \((\beta )\) là \(\vec n'\).
Nếu hai đường thẳng \(a\) và \(a'\) vuông góc với \((\alpha )\), và \(b\) và \(b'\) vuông góc với \((\beta )\), thì hai vectơ \(\vec n\) và \(\vec n'\)lần lượt là hai vectơ chỉ phương của \(a\) và \(a'\), \(b\) và \(b'\).
Mà góc giữa hai đường thẳng bằng góc giữa hai vectơ chỉ phương của chúng nên
\((a,b) = (a',b')\) do cùng bằng với góc \((\overrightarrow n ,\overrightarrow {n'} )\).
Vậy nếu \(\vec a\) vuông góc với \((\alpha )\) và \(\vec b\) vuông góc với \((\beta )\), thì hai góc \((a,b)\) và \((a',b')\) sẽ bằng nhau vì cùng liên quan đến vectơ pháp tuyến \(\vec n\) và \(\vec n'\).
Trả lời câu hỏi Luyện tập 3 trang 70 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tính góc giữa mặt phẳng \((\alpha ):\sqrt 3 x - y + 2 = 0\) và các mặt phẳng toạ độ \((Oxy)\), \((Oxz)\), \((Oyz)\).
Phương pháp giải:
- Xác định vectơ pháp tuyến của mặt phẳng \((\alpha )\).
- Góc giữa hai mặt phẳng là góc giữa các vectơ pháp tuyến của chúng:
\(\cos \theta = \frac{{{{\vec n}_1} \cdot {{\vec n}_2}}}{{|{{\vec n}_1}||{{\vec n}_2}|}}\)
Trong đó, \({\vec n_1} \cdot {\vec n_2}\) là tích vô hướng, \(|{\vec n_1}|\) và \(|{\vec n_2}|\) là độ lớn của các vectơ.
Lời giải chi tiết:
Cho mặt phẳng \((\alpha )\): \(\sqrt 3 x - y + 2 = 0\).
Vectơ pháp tuyến của mặt phẳng \(\alpha \): \({\vec n_\alpha } = (\sqrt 3 , - 1,0)\).
Góc giữa mặt phẳng \((\alpha )\) và Oxy:
- Vectơ pháp tuyến của Oxy: \({\vec n_{Oxy}} = (0,0,1)\).
Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oxy}} = \sqrt 3 .0 + ( - 1).0 + 0.1 = 0\)
Độ lớn:
\(|{\vec n_\alpha }| = \sqrt {3 + 1 + 0} = 2,\quad |{\vec n_{Oxy}}| = \sqrt {0 + 0 + 1} = 1\)
\(\cos \theta = \frac{0}{{2 \times 1}} = 0\quad \Rightarrow \theta = {90^\circ }\)
Góc giữa mặt phẳng \((\alpha )\) và Oxz:
- Vectơ pháp tuyến của Oxz: \({\vec n_{Oxz}} = (0,1,0)\).
Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oxz}} = \sqrt 3 .0 + ( - 1).1 + 0.0 = - 1\)
Độ lớn:
\(|{\vec n_{Oxz}}| = \sqrt {0 + 1 + 0} = 1\)
\(\cos \theta = \frac{{ - 1}}{{2 \times 1}} = - \frac{1}{2}\quad \Rightarrow \theta = {120^\circ }\)
Góc giữa mặt phẳng \((\alpha )\) và Oyz:
- Vectơ pháp tuyến của Oyz: \({\vec n_{Oyz}} = (1,0,0)\). Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oyz}} = \sqrt 3 .1 + ( - 1).0 + 0.0 = \sqrt 3 \)
Độ lớn:
\(|{\vec n_{Oyz}}| = \sqrt {1 + 0 + 0} = 1\)
\(\cos \theta = \frac{{\sqrt 3 }}{{2 \times 1}} = \frac{{\sqrt 3 }}{2}\quad \Rightarrow \theta = {30^\circ }\)
Trả lời câu hỏi Vận dụng trang 70 SGK Toán 12 Cùng khám phá
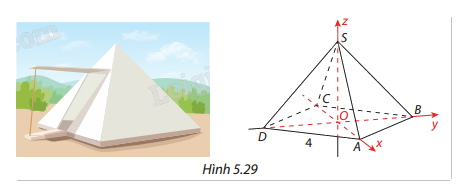
Để chuẩn bị cho chuyến đi dã ngoại, nhóm bạn Đức thiết kế lều cắm trại dạng hình chóp từ giác đều có đáy là hình vuông cạnh 4m. Theo bản vẽ thiết kế thì góc giữa hai mặt bên của lều bằng 60°. Bằng phương pháp tọa độ, hãy tính chiều cao của lều này.
Phương pháp giải:
- Xây dựng hệ tọa độ và xác định tọa độ các điểm
- Xác định vector pháp tuyến của các mặt bên
- Sử dụng công thức tính góc giữa hai mặt phẳng qua vector pháp tuyến
- Giải phương trình để tìm chiều cao
Lời giải chi tiết:
Gọi h là chiều cao cần tìm của hình chóp S.ABCD.
Do mặt đáy là hình vuông cạnh 4m nên \(OA = OB = OC = OD = 2\sqrt 2 \)
Toạ độ các điểm là \(A(2\sqrt 2 ;0;0)\), \(B(0;2\sqrt 2 ;0)\), \(C( - 2\sqrt 2 ;0;0)\), \(D(0; - 2\sqrt 2 ;0)\) và \(S(0;0;h)\).
Vectơ chỉ phương của mặt phẳng SAB là \(\overrightarrow {AB} = ( - 2\sqrt 2 ;2\sqrt 2 ;0)\) và \(\overrightarrow {SA} = (2\sqrt 2 ;0; - h)\)
Suy ra vectơ pháp tuyến của mặt phẳng SAB là
\(\overrightarrow {{n_{SAB}}} = \overrightarrow {AB} .\overrightarrow {SA} = (2\sqrt 2 .( - h) - 0.0;\,\,\,0.2\sqrt 2 - ( - 2\sqrt 2 ).( - h);\,\,\,( - 2\sqrt 2 ).0 - 2\sqrt 2 .2\sqrt 2 = ( - 2\sqrt 2 .h; - 2\sqrt 2 .h; - 8)\)
Vectơ chỉ phương của mặt phẳng SCD là \(\overrightarrow {DC} = ( - 2\sqrt 2 ;2\sqrt 2 ;0)\) và \(\overrightarrow {SC} = ( - 2\sqrt 2 ;0; - h)\)
Suy ra vectơ pháp tuyến của mặt phẳng SCD là
\(\overrightarrow {{n_{SCD}}} = \overrightarrow {DC} .\overrightarrow {SC} = (2\sqrt 2 .( - h) - 0.0;\,\,\,0.( - 2\sqrt 2 ) - ( - 2\sqrt 2 ).( - h);\,\,\,( - 2\sqrt 2 ).0 - 2\sqrt 2 .( - 2\sqrt 2 )) = ( - 2\sqrt 2 .h; - 2\sqrt 2 .h;8)\)
Ta có:
\(\overrightarrow {{n_{SAB}}} .\overrightarrow {{n_{SCD}}} = 8{h^2} + 8{h^2} - 64 = 16{h^2} - 64 = 16({h^2} - 4)\)
\(\left| {\overrightarrow {{n_{SAB}}} } \right| = \sqrt {8{h^2} + 8{h^2} + 64} = \sqrt {16{h^2} + 64} = 4\sqrt {{h^2} + 4} \)
\(\left| {\overrightarrow {{n_{SCD}}} } \right| = \sqrt {8{h^2} + 8{h^2} + 64} = \sqrt {16{h^2} + 64} = 4\sqrt {{h^2} + 4} \)
Góc giữa hai mặt phẳng SAB và SCD bằng 60° nên suy ra:
\(\cos 60^\circ = \frac{{16({h^2} - 4)}}{{4\sqrt {{h^2} + 4} .4\sqrt {{h^2} + 4} }} = \frac{{16({h^2} - 4)}}{{16({h^2} + 4)}} = \frac{{{h^2} - 4}}{{{h^2} + 4}} = \frac{1}{2}\)
\( \Leftrightarrow 2{h^2} - 8 = {h^2} + 4\)
\( \Leftrightarrow {h^2} = 12\)
\( \Leftrightarrow h = \sqrt {12} = 2\sqrt 3 \)
Vậy chiều cao của lều là \(2\sqrt 3 \)m.
Mục 3 trong SGK Toán 12 tập 2 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ đi sâu vào từng bài tập, cung cấp lời giải chi tiết và dễ hiểu, giúp các em tự tin hơn khi làm bài tập về nhà và chuẩn bị cho các kỳ thi.
Bài tập này yêu cầu học sinh giải các phương trình lượng giác cơ bản, sử dụng các công thức biến đổi lượng giác và các phương pháp giải phương trình quen thuộc. Ví dụ:
Phương pháp đặt ẩn phụ: Sử dụng khi phương trình có dạng phức tạp, có thể đưa về phương trình bậc hai hoặc phương trình đơn giản hơn bằng cách đặt ẩn phụ.
Sử dụng công thức lượng giác: Áp dụng các công thức cộng, trừ, nhân, chia góc, công thức hạ bậc, công thức nhân đôi để biến đổi phương trình về dạng đơn giản hơn.
Sử dụng đường tròn lượng giác: Tìm các giá trị của góc thỏa mãn phương trình bằng cách xác định vị trí trên đường tròn lượng giác.
Bài tập này thường yêu cầu học sinh sử dụng các kỹ năng giải phương trình lượng giác phức tạp hơn, kết hợp nhiều phương pháp và công thức khác nhau. Ví dụ:
Phương pháp đổi biến: Sử dụng khi phương trình có dạng đặc biệt, có thể đưa về phương trình quen thuộc bằng cách đổi biến.
Sử dụng tính chất đối xứng của hàm số lượng giác: Tìm các nghiệm của phương trình bằng cách sử dụng tính chất đối xứng của hàm số lượng giác.
Sử dụng phương pháp đánh giá: Đánh giá giá trị của biểu thức lượng giác để tìm ra khoảng giá trị của nghiệm.
Bài tập này yêu cầu học sinh áp dụng kiến thức về phương trình lượng giác để giải các bài toán thực tế, ví dụ như bài toán về dao động điều hòa, bài toán về góc và khoảng cách. Để giải quyết các bài toán này, học sinh cần phân tích đề bài, xác định các yếu tố liên quan đến lượng giác và xây dựng phương trình phù hợp.
Để đạt kết quả tốt nhất khi giải bài tập mục 3 trang 69, 70 SGK Toán 12 tập 2, học sinh cần:
Nắm vững lý thuyết: Hiểu rõ các định nghĩa, định lý, công thức và phương pháp giải liên quan đến phương trình lượng giác.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Sử dụng các nguồn tài liệu tham khảo: Tham khảo thêm các sách giáo khoa, tài liệu tham khảo, bài giảng trực tuyến để hiểu rõ hơn về kiến thức.
Hy vọng bài giải chi tiết mục 3 trang 69, 70 SGK Toán 12 tập 2 tại giaitoan.edu.vn sẽ giúp các em học sinh hiểu rõ hơn về kiến thức và rèn luyện kỹ năng giải toán. Chúc các em học tập tốt!