Chào mừng các em học sinh đến với bài giải bài tập 1.17 trang 22 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
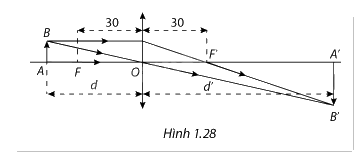
Một thấu kính hội tụ có tiêu cự f=30cm như hình 1.28. Trong vật lý, ta biết rằng nếu đặt vật thật AB cách quang tâm O của thấu kính một khoảng d(cm) lơn hơn 30cm thì được ảnh thật A’B’ cách quang tâm của thấu kính một khoảng d’(cm). Ngược lại, nếu 0<d<30 thì ta có ảnh ảo. Công thức thấu kính là \(\frac{1}{d} + \frac{1}{{d'}} = \frac{{\rm{1}}}{{\rm{f}}}\). a) Từ công thức thấu kính, tìm biểu thức xác định d’ theo d. b) Xem biểu thức của d’ ở câu a là một hàm số theo d, kí hiệu là h(d). Tìm các
Đề bài
Một thấu kính hội tụ có tiêu cự f=30cm như hình 1.28. Trong vật lý, ta biết rằng nếu đặt vật thật AB cách quang tâm O của thấu kính một khoảng d(cm) lơn hơn 30cm thì được ảnh thật A’B’ cách quang tâm của thấu kính một khoảng d’(cm). Ngược lại, nếu 0<d<30 thì ta có ảnh ảo. Công thức thấu kính là \(\frac{1}{d} + \frac{1}{{d'}} = \frac{{\rm{1}}}{{\rm{f}}}\).
a) Từ công thức thấu kính, tìm biểu thức xác định d’ theo d.
b) Xem biểu thức của d’ ở câu a là một hàm số theo d, kí hiệu là h(d). Tìm các đường tiệm cận của h(d).
Phương pháp giải - Xem chi tiết
Từ công thức \(\frac{1}{d} + \frac{1}{{d'}} = \frac{{\rm{1}}}{{\rm{f}}}\) rút ra d’.
Tìm \(h\left( d \right)\;\), \(h\left( d \right)\;\).
Lời giải chi tiết
a) Ta có: \(\frac{1}{d} + \frac{1}{{d'}} = \frac{{\rm{1}}}{{\rm{f}}} = \frac{1}{{30}}\)
\( \Rightarrow \frac{1}{{d'}} = \frac{{\rm{1}}}{{30}} - \frac{1}{d} = \frac{{d - 30}}{{30d}}\)
\( \Rightarrow d' = \frac{{30d}}{{d - 30}}\)
b) Ta có \(h(d) = \frac{{30d}}{{d - 30}}\)
c) \(\mathop {\lim }\limits_{d \to + \infty } h\left( d \right)\;\; = \mathop {\lim }\limits_{d \to + \infty } \frac{{30}}{{1 - \frac{3}{d}}} = 30\;\)
Suy ra y = 30 là đường tiệm cận ngang của hàm số.
\(\mathop {\lim }\limits_{d \to {{30}^ + }} h\left( d \right)\;\; = \mathop {\lim }\limits_{d \to {{30}^ + }} \frac{{30d}}{{d - 30}} = + \infty \;,\mathop {\lim }\limits_{d \to {{30}^ - }} h\left( d \right)\;\; = \mathop {\lim }\limits_{d \to {{30}^ - }} \frac{{30d}}{{d - 30}} = - \infty \;\)
Suy ra x = 30 là đường tiệm cận đứng của h(d).
Bài tập 1.17 trang 22 SGK Toán 12 tập 1 yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết một bài toán thực tế liên quan đến tốc độ thay đổi của một đại lượng. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và công thức đạo hàm cơ bản, cũng như kỹ năng phân tích và giải quyết bài toán.
Bài tập thường đề cập đến một tình huống cụ thể, ví dụ như một vật thể chuyển động, một quá trình tăng trưởng, hoặc một sự thay đổi nào đó. Học sinh cần xác định được hàm số mô tả đại lượng cần tìm, sau đó tính đạo hàm của hàm số đó để tìm ra tốc độ thay đổi của đại lượng tại một thời điểm hoặc một vị trí nhất định.
Giả sử bài tập yêu cầu tính vận tốc của một vật thể tại thời điểm t, biết rằng quãng đường vật thể đi được là hàm số s(t) = 2t2 + 3t + 1. Để giải bài tập này, chúng ta thực hiện các bước sau:
Bài tập 1.17 trang 22 SGK Toán 12 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải quyết bài toán thực tế. Bằng cách nắm vững phương pháp giải và luyện tập thường xuyên, các em sẽ tự tin hơn trong việc học tập môn Toán.
| Công thức đạo hàm cơ bản | Ví dụ |
|---|---|
| Đạo hàm của hằng số | (c)' = 0 |
| Đạo hàm của hàm số lũy thừa | (xn)' = nxn-1 |
| Đạo hàm của tổng | (u + v)' = u' + v' |