Chào mừng các em học sinh đến với bài giải chi tiết bài tập 2.21 trang 80 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác, dễ hiểu và các phương pháp giải bài tập hiệu quả.
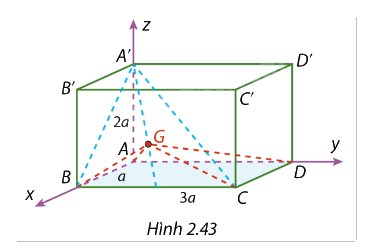
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A'B'C'D' có đỉnh A trùng với gốc tọa độ và các đỉnh B, D, A' tương ứng thuộc các tia Ox, Oy, Oz như trong Hình 2.43. Cho biết AB = a, AD = 3a, AA' = 2a \ (a > 0). Gọi G là trọng tâm của tam giác A'BC. a) Tìm toạ độ điểm G. b) Tính khoảng cách từ G đến mặt phẳng (ABCD). c) Tính thể tích khóp G.ABCD.
Đề bài
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A'B'C'D' có đỉnh A trùng với gốc tọa độ và các đỉnh B, D, A' tương ứng thuộc các tia Ox, Oy, Oz như trong Hình 2.43. Cho biết AB = a, AD = 3a, AA' = 2a \ (a > 0). Gọi G là trọng tâm của tam giác A'BC.
a) Tìm toạ độ điểm G.
b) Tính khoảng cách từ G đến mặt phẳng (ABCD).
c) Tính thể tích khóp G.ABCD.
Phương pháp giải - Xem chi tiết
a) Sử dụng công thức trọng tâm của tam giác trong không gian Oxyz.
b) Sử dụng công thức khoảng cách từ một điểm đến một mặt phẳng trong không gian.
c) Sử dụng công thức thể tích khối chóp trong không gian.
Lời giải chi tiết
a) Tọa độ các điểm \(B(a;0;0)\), \(C(0;3a;0)\), \(A'(0;0;2a)\). Tọa độ của điểm \(G\) - trọng tâm tam giác A'BC:
\(G\left( {\frac{{0 + a + 0}}{3},\frac{{0 + 0 + 3a}}{3},\frac{{2a + 0 + 0}}{3}} \right) = G\left( {\frac{a}{3};a;\frac{{2a}}{3}} \right)\)
b) Phương trình mặt phẳng \((ABCD)\) là: \(z = 0\). Khoảng cách từ \(G\left( {\frac{a}{3};a;\frac{{2a}}{3}} \right)\) đến mặt phẳng \((ABCD)\) là:
\(d = \left| {\frac{{2a}}{3} - 0} \right| = \frac{{2a}}{3}\)
c) Thể tích khối chóp G.ABCD: Sử dụng công thức thể tích khối chóp với chiều cao là khoảng cách từ \(G\) đến mặt phẳng \((ABCD)\) và diện tích đáy là diện tích hình chữ nhật ABCD:
\(V = \frac{1}{3} \times {S_{ABCD}} \times d = \frac{1}{3} \times (AB \times AD) \times \frac{{2a}}{3} = \frac{1}{3} \times a \times 3a \times \frac{{2a}}{3} = \frac{{2{a^3}}}{3}\)
Bài tập 2.21 trang 80 SGK Toán 12 tập 1 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm, điều kiện cực trị và cách xác định khoảng đồng biến, nghịch biến của hàm số.
Đề bài: Cho hàm số y = f(x) = x3 - 3x2 + 2. Hãy tìm các điểm cực trị của hàm số.
Phân tích: Để tìm các điểm cực trị, chúng ta cần thực hiện các bước sau:
Bước 1: Tính đạo hàm bậc nhất
f'(x) = 3x2 - 6x
Bước 2: Tìm các điểm mà f'(x) = 0
3x2 - 6x = 0
3x(x - 2) = 0
Suy ra x = 0 hoặc x = 2
Bước 3: Khảo sát dấu của f'(x)
Ta lập bảng xét dấu f'(x):
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Từ bảng xét dấu, ta thấy:
Kết luận: Hàm số y = x3 - 3x2 + 2 đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.
Để hiểu sâu hơn về cách giải bài tập khảo sát hàm số, các em có thể tham khảo thêm các bài tập tương tự sau:
Ngoài ra, các em cũng có thể tìm hiểu thêm về các phương pháp giải bài tập khảo sát hàm số trên các trang web học toán online uy tín như giaitoan.edu.vn. Chúng tôi luôn cập nhật những lời giải chi tiết, dễ hiểu và các phương pháp giải bài tập hiệu quả để giúp các em học tập tốt hơn.
Khi giải bài tập khảo sát hàm số, các em cần lưu ý những điều sau:
Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!