Chào mừng các em học sinh đến với bài giải bài tập 4.20 trang 31 SGK Toán 12 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
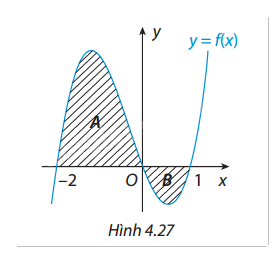
Cho hàm số \(y = f(x)\) có đồ thị như Hình 4.27 và diện tích hai phần \[A,{\rm{ }}B\] lần lượt bằng 11 và 2. Tính \(\int_{ - 2}^1 f (x)dx\).
Đề bài
Cho hàm số \(y = f(x)\) có đồ thị như Hình 4.27 và diện tích hai phần \(A,{\rm{ }}B\) lần lượt bằng 11 và 2. Tính \(\int_{ - 2}^1 f (x)dx\).
Phương pháp giải - Xem chi tiết
- Xác định dấu của \(f(x)\) trên các khoảng \([ - 2,0]\) và \([0,1]\).
- Tính tích phân từ -2 đễn 1 dựa vào diện tích đã cho.
Lời giải chi tiết
- Từ đồ thi, \(A\) ở bên trái trục tung \((x = 0)\) và diện tích của \(A\) là 11 (dương).
- Phằn \(B\) nằm phía bên phải và diện tích của \(B\) là 2 (âm do đồ thị ở dưới trục \(x\)).
- Tích phân từ -2 đến 1 của \(f(x)\):
\(\int_{ - 2}^1 f (x)dx = 11 - 2 = 9\).
Bài tập 4.20 trang 31 SGK Toán 12 tập 2 là một bài toán quan trọng trong chương trình học về đạo hàm. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm của hàm số, các quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hàm số y = f(x) có đạo hàm f'(x) = (x-1)^2(x+2). Hỏi hàm số y = f(x) đồng biến trên khoảng nào?)
Để giải bài tập này, chúng ta cần xác định khoảng mà trên đó đạo hàm f'(x) dương. Hàm số y = f(x) đồng biến trên khoảng (a, b) nếu f'(x) > 0 với mọi x thuộc (a, b).
Ta có f'(x) = (x-1)^2(x+2). Để f'(x) > 0, ta cần xét dấu của f'(x). Vì (x-1)^2 luôn dương với mọi x khác 1, nên dấu của f'(x) phụ thuộc vào dấu của (x+2).
Vậy, hàm số y = f(x) đồng biến trên khoảng (-2, 1) và (1, +∞).
Khi xét dấu của đạo hàm, cần chú ý đến các điểm mà đạo hàm bằng 0 hoặc không xác định. Tại các điểm này, hàm số có thể không đồng biến hoặc nghịch biến.
Để củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm, các em có thể tham khảo các bài tập tương tự sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài tập 4.20 trang 31 SGK Toán 12 tập 2 là một bài toán quan trọng giúp các em hiểu rõ hơn về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các em sẽ tự tin hơn khi giải các bài tập tương tự.
| Khái niệm | Công thức |
|---|---|
| Đạo hàm | f'(x) = lim (h->0) [f(x+h) - f(x)] / h |
| Đạo hàm của hàm số lũy thừa | (x^n)' = nx^(n-1) |
| Đạo hàm của hàm số lượng giác | (sin x)' = cos x, (cos x)' = -sin x |