Chào mừng các em học sinh đến với bài giải chi tiết bài tập 5.29 trang 71 SGK Toán 12 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12, tập trung vào kiến thức về số phức và các phép toán liên quan.
Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
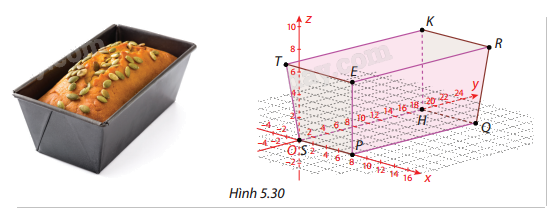
Một khuôn nướng bánh mì được mô phỏng trong không gian Oxyz như Hình 5.30 với các điểm sau: \(S(0;0;0)\), \(P(8;0;0)\), \(Q(8;18;0)\), \(T( - 1; - 1;7)\), \(R(9;19;7)\). Tính góc giữa hai cạnh kề nhau, giữa cạnh bên và mặt đáy, giữa mặt bên và mặt đáy của khuôn.
Đề bài
Một khuôn nướng bánh mì được mô phỏng trong không gian Oxyz như Hình 5.30 với các điểm sau: \(S(0;0;0)\), \(P(8;0;0)\), \(Q(8;18;0)\), \(T( - 1; - 1;7)\), \(R(9;19;7)\). Tính góc giữa hai cạnh kề nhau, giữa cạnh bên và mặt đáy, giữa mặt bên và mặt đáy của khuôn.
Phương pháp giải - Xem chi tiết
1. Tính góc giữa hai cạnh kề
- Xác định vectơ chỉ phương của hai cạnh:
- Sử dụng công thức tính góc giữa hai vectơ:
\(\cos \theta = \frac{{\vec u \cdot \vec v}}{{|\vec u||\vec v|}}\)
2. Tính góc giữa cạnh bên và mặt đáy:
- Xác định các vectơ chỉ phương của cạnh bên và mặt đáy.
- Sử dụng công thức tính góc giữa hai vectơ:
\(\cos \theta = \frac{{\vec u \cdot \vec v}}{{|\vec u||\vec v|}}\)
3. Tính góc giữa mặt bên và mặt đáy:
- Tính vectơ pháp tuyến của mặt bên và mặt đáy.
- Sử dụng công thức tính góc giữa hai mặt phẳng:
\(\cos \theta = \frac{{|\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} |}}{{|\overrightarrow {{n_1}} ||\overrightarrow {{n_2}} |}}\)
Lời giải chi tiết
- Tính góc giữa hai cạnh kề nhau:
Ta có các vectơ chỉ phương sau:
\(\overrightarrow {SP} = P - S = (8 - 0;0 - 0;0 - 0) = (8;0;0)\)
\(\overrightarrow {SQ} = Q - S = (8 - 0;18 - 0;0 - 0) = (8;18;0)\)
\(\overrightarrow {ST} = T - S = ( - 1 - 0; - 1 - 0;7 - 0) = ( - 1; - 1;7)\)
\(\overrightarrow {SH} = \overrightarrow {PQ} = (0;18;0)\)
\(\overrightarrow {SE} = (9; - 1;7)\)
Góc giữa những cặp cạnh kề nhau:
\(\begin{array}{l}\cos (\overrightarrow {SP} ,\overrightarrow {ST} ) = \frac{{8.( - 1) + 0.( - 1) + 0.( - 7)}}{{\sqrt {{8^2}} .\sqrt {{{( - 1)}^2} + {{( - 1)}^2} + {{( - 7)}^2}} }} = \frac{{ - 8}}{{8.\sqrt {51} }} = \frac{{ - 1}}{{\sqrt {51} }} \Rightarrow (\overrightarrow {SP} ,\overrightarrow {ST} ) \approx {98^\circ }\\ \Leftrightarrow (\overrightarrow {PS} ,\overrightarrow {PE} ) = (\overrightarrow {HQ} ,\overrightarrow {HK} ) = (\overrightarrow {QH} ,\overrightarrow {QR} ) \approx {98^\circ }\end{array}\)
\(\begin{array}{l}\cos (\overrightarrow {EP} ,\overrightarrow {ER} ) = \frac{{( - 1).(0) + (1).(2) + ( - 7).(0)}}{{\sqrt {{{( - 1)}^2} + {1^2} + {{( - 7)}^2}} .\sqrt {{0^2} + {2^2} + {0^2}} }} = \frac{2}{{\sqrt {51} .2}} = \frac{1}{{\sqrt {51} }} \Rightarrow (\overrightarrow {EP} ,\overrightarrow {ER} ) \approx {82^\circ }\\ \Leftrightarrow (\overrightarrow {RE} ,\overrightarrow {RQ} ) = (\overrightarrow {TS} ,\overrightarrow {TK} ) = (\overrightarrow {KT} ,\overrightarrow {KH} ) \approx {82^\circ }\end{array}\)
\(\begin{array}{l}\cos (\overrightarrow {ET} ,\overrightarrow {EP} ) = \frac{{( - 10).( - 1) + (0).(1) + (0).( - 7)}}{{\sqrt {{{( - 10)}^2} + {0^2} + {0^2}} .\sqrt {{{( - 1)}^2} + {1^2} + {{( - 7)}^2}} }} = \frac{{10}}{{10.\sqrt {51} }} = \frac{1}{{\sqrt {51} }} \Rightarrow (\overrightarrow {ET} ,\overrightarrow {EP} ) \approx {82^\circ }\\ \Leftrightarrow (\overrightarrow {TE} ,\overrightarrow {TS} ) = (\overrightarrow {KH} ,\overrightarrow {KR} ) = (\overrightarrow {RK} ,\overrightarrow {RQ} ) \approx {82^\circ }\end{array}\)
\(\begin{array}{l}\cos (\overrightarrow {PE} ,\overrightarrow {PQ} ) = \frac{{(1).(0) + ( - 1).(18) + (7).(0)}}{{\sqrt {{1^2} + {{( - 1)}^2} + {7^2}} .\sqrt {{0^2} + {{18}^2} + {0^2}} }} = \frac{{ - 18}}{{\sqrt {51} .18}} = \frac{{ - 1}}{{\sqrt {51} }} \Rightarrow (\overrightarrow {PE} ,\overrightarrow {PQ} ) \approx {98^\circ }\\ \Leftrightarrow (\overrightarrow {QP} ,\overrightarrow {QR} ) = (ST,\overrightarrow {SH} ) = (\overrightarrow {HS} ,\overrightarrow {HK} ) \approx {98^\circ }\end{array}\)
\(\cos (\overrightarrow {SP} ,\overrightarrow {SH} ) = \frac{{8.(0) + 0.(18) + 0.(0)}}{{\sqrt {{8^2}} .\sqrt {{0^2} + {{18}^2} + {0^2}} }} = 0 \Rightarrow (\overrightarrow {SP} ,\overrightarrow {SH} ) = {90^\circ }\)
\(\cos (\overrightarrow {PS} ,\overrightarrow {PQ} ) = \frac{{( - 8).(0) + 0.(18) + 0.(0)}}{{\sqrt {{{( - 8)}^2}} .\sqrt {{0^2} + {{18}^2} + {0^2}} }} = 0 \Rightarrow (\overrightarrow {PS} ,\overrightarrow {PQ} ) = {90^\circ }\)
Các cặp cạnh còn lại có số đo góc là 90°
- Tính góc giữa cạnh bên và mặt đáy:
Chọn một cạnh bên là ST.
Vectơ pháp tuyến của mặt đáy SPQH là:
\(\vec n = \overrightarrow {SP} \times \overrightarrow {SQ} = (0.0 - 0.18;0.8 - 8.0;8.18 - 0.8) = (0;0;144)\)
\( \Rightarrow \theta = \arccos \left( {\frac{7}{{\sqrt {51} }}} \right)\)
- Tính góc giữa mặt bên và mặt đáy của khuôn.
Chọn mặt bên là STEP
Vectơ pháp tuyến của mặt phẳng STEP là:
\(\overrightarrow {{n_{STEP}}} = \overrightarrow {SP} .\overrightarrow {ST} = (0.7 - 0.( - 1);0.( - 1) - 8.7;8.( - 1) - 0.( - 1)) = (0; - 56; - 8)\)
Góc giữa mặt bên STEP và mặt đáy SPQH là:
\(\cos \theta = \frac{{\left| {0.0 + 0.( - 56) + 144.( - 8)} \right|}}{{\sqrt {{{144}^2}} .\sqrt {{{( - 56)}^2} + {{( - 8)}^2}} }} = \frac{{1208}}{{144.40\sqrt 2 }} = \frac{{151}}{{720\sqrt 2 }} \Rightarrow \theta \approx 81^\circ \)
Bài tập 5.29 trang 71 SGK Toán 12 tập 2 yêu cầu tìm số phức z thỏa mãn một phương trình hoặc hệ phương trình liên quan đến số phức. Để giải bài tập này, chúng ta cần nắm vững các kiến thức cơ bản về số phức, bao gồm:
Tùy thuộc vào dạng bài cụ thể, phương pháp giải có thể khác nhau. Dưới đây là một số phương pháp thường được sử dụng:
Bài toán: Tìm số phức z thỏa mãn |z - (1 + i)| = 2.
Giải:
Đặt z = x + yi, với x, y là các số thực. Khi đó, |z - (1 + i)| = |(x - 1) + (y - 1)i| = √((x - 1)2 + (y - 1)2). Theo đề bài, ta có:
√((x - 1)2 + (y - 1)2) = 2
Bình phương hai vế, ta được:
(x - 1)2 + (y - 1)2 = 4
Đây là phương trình đường tròn tâm I(1, 1) bán kính R = 2 trên mặt phẳng phức. Vậy, số phức z thỏa mãn bài toán là các số phức có điểm biểu diễn nằm trên đường tròn này.
Để củng cố kiến thức và kỹ năng giải bài tập về số phức, các em có thể luyện tập thêm các bài tập tương tự trong SGK Toán 12 tập 2 và các tài liệu tham khảo khác. Hãy chú trọng việc nắm vững các kiến thức cơ bản và rèn luyện kỹ năng giải toán thường xuyên.
Bài tập 5.29 trang 71 SGK Toán 12 tập 2 là một bài tập quan trọng giúp các em hiểu sâu hơn về số phức và các phép toán liên quan. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em có thể tự tin giải bài tập này và các bài tập tương tự một cách hiệu quả. Chúc các em học tốt!
Lưu ý: Bài giải trên chỉ là một ví dụ minh họa cho một dạng bài cụ thể. Các em cần xem lại đề bài gốc để áp dụng phương pháp giải phù hợp.