Chào mừng các em học sinh đến với bài giải bài tập 1.39 trang 47 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12 tập 1, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
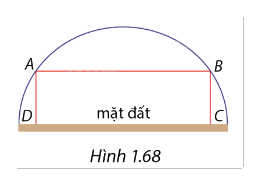
Một cổng vòm có dạng nửa hình tròn trên mặt đất với bán kính R=5 m. Người ta muốn đặt một khung hình chữ nhật ABCD để thiết kế trang trí, với hai điểm A,B đính trên vòm và CD đặt trên mặt đất (Hình 1.68). Tìm khoảng cách A,B so với mặt đất để diện tích hình chữ nhật ABCD là lớn nhất.
Đề bài
Một cổng vòm có dạng nửa hình tròn trên mặt đất với bán kính R=5 m. Người ta muốn đặt một khung hình chữ nhật ABCD để thiết kế trang trí, với hai điểm A,B đính trên vòm và CD đặt trên mặt đất (Hình 1.68). Tìm khoảng cách A,B so với mặt đất để diện tích hình chữ nhật ABCD là lớn nhất.
Phương pháp giải - Xem chi tiết
- Đặt y (m) là khoảng cách từ AB đến mặt đất. Vì A và B nằm trên vòm nửa hình tròn có bán kính R=5 m, nên tọa độ của A và B có thể biểu diễn dưới dạng (x,y).
- Tìm phương trình đường tròn và tính diện tích S của hình chữ nhật ABCD.
- Biểu diễn S dưới dạng một hàm của y và cực đại hóa S bằng cách tìm đạo hàm.
Lời giải chi tiết
Gọi y (m) là khoảng cách từ A và B đến mặt đất (y>0).
Vì A và B nằm trên nửa hình tròn có tâm tại gốc tọa độ (0,0) và bán kính R=5 m, tọa độ của chúng thỏa mãn phương trình đường tròn:
\({x^2} + {y^2} = 25\)
Giả sử A có toạ độ \(( - x,y)\) và B có toạ độ \((x,y)\).
Chiều dài AB là: \(\sqrt {{{( - x - x)}^2} + {{(y - y)}^2}} = 2x\)
Diện tích hình chữ nhật ABCD là: \(S = AB.AD = 2xy\)
Thay \(x = \sqrt {25 - {y^2}} \) vào biểu thức diện tích ta được: \(S = 2\sqrt {25 - {y^2}} .y\)
Đạo hàm của S theo y: \(\)\(S' = 2\left( {\sqrt {25 - {y^2}} + y.\frac{{ - y}}{{\sqrt {25 - {y^2}} }}} \right) = 2\left( {\frac{{25 - {y^2} - {y^2}}}{{\sqrt {25 - {y^2}} }}} \right) = 2\left( {\frac{{25 - 2{y^2}}}{{\sqrt {25 - {y^2}} }}} \right)\)
Đặt đạo hàm bằng 0, ta có: \(S' = 0 \Leftrightarrow 25 - 2{y^2} = 0 \Leftrightarrow 2{y^2} = 25 \Rightarrow y = \frac{{5\sqrt 2 }}{2}\)
Đạo hàm cấp 2 của S:
\(\begin{array}{l}S'' = 2.\frac{{ - 4y.\sqrt {25 - {y^2}} + (25 - 2{y^2})\frac{y}{{\sqrt {25 - {y^2}} }}}}{{25 - {y^2}}}\\ = 2.\frac{{ - 4y\sqrt {25 - {y^2}} + \frac{{y\left( {25 - 2{y^2}} \right)}}{{\sqrt {25 - {y^2}} }}}}{{25 - {y^2}}}\\ = 2.\frac{{ - 4y\left( {25 - {y^2}} \right) + y\left( {25 - 2{y^2}} \right)}}{{\left( {25 - {y^2}} \right)\sqrt {25 - {y^2}} }}\\ = 2.\frac{{ - 4y\left( {25 - {y^2}} \right) + y\left( {25 - 2{y^2}} \right)}}{{\left( {25 - {y^2}} \right)\sqrt {25 - {y^2}} }}\\ = 2.\frac{{ - 100y + 4{y^3} + 25y - 2{y^3}}}{{\left( {25 - {y^2}} \right)\sqrt {25 - {y^2}} }}\\ = 2.\frac{{ - 75y + 2{y^3}}}{{\left( {25 - {y^2}} \right)\sqrt {25 - {y^2}} }}\end{array}\)
Thay \(y = \frac{{5\sqrt 2 }}{2}\) vào đạo hàm cấp 2 ta được:
\(S''\left( {\frac{{5\sqrt 2 }}{2}} \right) = 2.\frac{{ - 75.\left( {\frac{{5\sqrt 2 }}{2}} \right) + 2{{\left( {\frac{{5\sqrt 2 }}{2}} \right)}^3}}}{{\left( {25 - {{\left( {\frac{{5\sqrt 2 }}{2}} \right)}^2}} \right)\sqrt {25 - {{\left( {\frac{{5\sqrt 2 }}{2}} \right)}^2}} }} = - 8 < 0\)
Vì giá trị âm nên \(y = \frac{{5\sqrt 2 }}{2}\)là cực đại của hàm S.
Vậy A, B cách mặt đất một khoảng \(y = \frac{{5\sqrt 2 }}{2}\) thì diện tích hình chữ nhật ABCD là lớn nhất.
Bài tập 1.39 trang 47 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học về đạo hàm. Bài toán này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết một bài toán thực tế liên quan đến tốc độ thay đổi của một đại lượng nào đó.
(Đề bài sẽ được chèn vào đây - ví dụ: Một vật chuyển động theo phương trình s(t) = t3 - 3t2 + 5t + 2, trong đó s(t) là quãng đường đi được sau thời gian t. Hãy tìm vận tốc của vật tại thời điểm t = 2.)
Để giải bài tập này, chúng ta cần thực hiện các bước sau:
(Lời giải chi tiết sẽ được chèn vào đây, bao gồm các bước tính toán cụ thể và giải thích rõ ràng. Ví dụ:
s(t) = t3 - 3t2 + 5t + 2
v(t) = s'(t) = 3t2 - 6t + 5
v(2) = 3(2)2 - 6(2) + 5 = 12 - 12 + 5 = 5
Vậy vận tốc của vật tại thời điểm t = 2 là 5 đơn vị quãng đường/thời gian.)
Các bài tập tương tự thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến:
Để giải tốt các bài tập về đạo hàm, các em cần:
Ngoài SGK Toán 12 tập 1, các em có thể tham khảo thêm các tài liệu sau:
Bài tập 1.39 trang 47 SGK Toán 12 tập 1 là một bài tập quan trọng giúp các em củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán 12.