Chào mừng các em học sinh đến với bài giải chi tiết bài tập 5.22 trang 65 SGK Toán 12 tập 2. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Giả sử một máy bay thương mại M đang bay trên bầu trời theo một đường thẳng từ D đến E có hình chiếu trên mặt đất là đoạn CB. Tại D, máy bay bay cách mặt đất là 9000 m và tại E là 12000 m. Một ra-đa được đặt trên mặt đất tại vị trí O cách C là 20000 m, cách B là 16000 m và (widehat {BOC} = {90^^circ }). Xét hệ trục tọa độ Oxyz (đơn vị: 1000 m) với O là vị trí đặt ra-đa, B thuộc tia Oy, C thuộc tia Ox, khi đó ta có tọa độ các điểm như Hình 5.24. Giả sử ra-đa có bán kính dò tìm tối đa là 1600
Đề bài
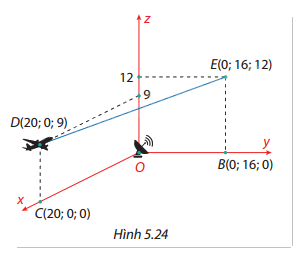
Giả sử một máy bay thương mại M đang bay trên bầu trời theo một đường thẳng từ D đến E có hình chiếu trên mặt đất là đoạn CB. Tại D, máy bay bay cách mặt đất là 9000 m và tại E là 12000 m. Một ra-đa được đặt trên mặt đất tại vị trí O cách C là 20000 m, cách B là 16000 m và \(\widehat {BOC} = {90^\circ }\). Xét hệ trục tọa độ Oxyz (đơn vị: 1000 m) với O là vị trí đặt ra-đa, B thuộc tia Oy, C thuộc tia Ox, khi đó ta có tọa độ các điểm như Hình 5.24. Giả sử ra-đa có bán kính dò tìm tối đa là 16000 m. Hỏi ra-đa này có thể dò tìm được tín hiệu của máy bay M khi bay trên bầu trời từ D đến E hay không? Vì sao?
Phương pháp giải - Xem chi tiết
- Viết phương trình tham số của đường thẳng DE từ tọa độ điểm \(D\) và \(E\).
- Sử dụng công thức khoảng cách từ điểm \(O\) đến đường thẳng DE trong không gian. Nếu khoảng cách nhỏ hơn hoặc bằng bán kính dò tìm \(16000{\mkern 1mu} m\), ra-đa sẽ bắt được tín hiệu máy bay.
Lời giải chi tiết
Tọa độ điểm \(D(20;0;9)\) và \(E(0;16;12)\). Vectơ chỉ phương của đường thẳng DE là:
\(\overrightarrow {DE} = (0 - 20;16 - 0;12 - 9) = ( - 20;16;3)\)
Phương trình tham số của đường thẳng DE:
\(\left\{ {\begin{array}{*{20}{l}}{x = 20 - 20t}\\{y = 16t}\\{z = 9 + 3t}\end{array}} \right.\)
trong đó t là tham số.
Gọi H là hình chiếu của O trên đường thẳng DE, suy ra toạ độ điểm M là:
\(H(20 - 20t;16t;9 + 3t)\)
Và tích vô hướng của \(\overrightarrow {OH} \) và \(\overrightarrow {DE} \) là:
\(\overrightarrow {DE} .\overrightarrow {OH} = ( - 20).(20 - 20t) + 16.16t + 3.(9 + 3t) = 0\)
Giải phương trình trên ta được điểm \(t = \frac{{373}}{{665}}\)
Điểm H có toạ độ là \(\left( {\frac{{1168}}{{133}};\frac{{5968}}{{665}};\frac{{7104}}{{665}}} \right)\)
Khoảng cách từ O đến đến đường thẳng DE chính là độ dài đoạn thẳng OH
\(d = \sqrt {{{\left( {\frac{{1168}}{{133}}} \right)}^2} + {{\left( {\frac{{5968}}{{665}}} \right)}^2} + {{\left( {\frac{{7104}}{{665}}} \right)}^2}} \approx 16,486 = 16486m\)
Vì khoảng cách từ ra-da tới đường bay của máy bay M lớn hơn bán kính dò tìm tối đa của ra-da nên không thể thấy tín hiệu của máy bay M.
Bài tập 5.22 trang 65 SGK Toán 12 tập 2 yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để tìm cực trị và khảo sát hàm số. Đây là một dạng bài tập quan trọng, thường xuyên xuất hiện trong các kỳ thi THPT Quốc gia.
Cho hàm số y = f(x) = x3 - 3x2 + 2. Hãy tìm:
Bước 1: Tìm tập xác định của hàm số
Hàm số y = f(x) = x3 - 3x2 + 2 là hàm đa thức, do đó tập xác định của hàm số là D = ℝ.
Bước 2: Tính đạo hàm bậc nhất của hàm số
f'(x) = 3x2 - 6x
Bước 3: Tìm các điểm cực trị của hàm số
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Suy ra x = 0 hoặc x = 2
Bước 4: Xác định loại cực trị
Ta xét dấu của f'(x) trên các khoảng:
Vậy hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
Bước 5: Tính giá trị của hàm số tại các điểm cực trị
f(0) = 03 - 3(0)2 + 2 = 2
f(2) = 23 - 3(2)2 + 2 = 8 - 12 + 2 = -2
Bước 6: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-1; 2]
Ta tính giá trị của hàm số tại các điểm đầu mút của đoạn và các điểm cực trị nằm trong đoạn:
So sánh các giá trị, ta thấy:
Giá trị lớn nhất của hàm số trên đoạn [-1; 2] là 2 (đạt được tại x = 0).
Giá trị nhỏ nhất của hàm số trên đoạn [-1; 2] là -2 (đạt được tại x = -1 và x = 2).
Hàm số y = f(x) = x3 - 3x2 + 2 đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2. Trên đoạn [-1; 2], giá trị lớn nhất của hàm số là 2 và giá trị nhỏ nhất là -2.
Để giải quyết các bài toán về khảo sát hàm số và tìm cực trị, học sinh cần nắm vững các kiến thức sau:
Hy vọng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về cách giải bài tập 5.22 trang 65 SGK Toán 12 tập 2. Chúc các em học tập tốt!