Chào mừng các em học sinh đến với bài giải bài tập 1.3 trang 9 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài viết này cung cấp lời giải chi tiết, dễ hiểu, giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ các em học tập tốt môn Toán. Hãy cùng khám phá bài giải ngay sau đây!
a) (y = frac{x}{3}{(x - 3)^2}) b) (y = left| x right|) c) (y = {3^{x - 2{x^2}}}) d) (y = ln ({x^2} + e))
Đề bài
a) \(y = \frac{x}{3}{(x - 3)^2}\)
b) \(y = \left| x \right|\)
c) \(y = {3^{x - 2{x^2}}}\)
d) \(y = \ln ({x^2} + e)\)
Phương pháp giải - Xem chi tiết
Bước 1: Tính \(y'\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định cực trị của hàm số dựa vào bảng biến thiên
Lời giải chi tiết
a) \(y = \frac{x}{3}{(x - 3)^2}\)
Hàm số trên xác định trên R
Ta có: \(y' = \frac{{{{(x - 3)}^2}}}{3} + \frac{{x.2(x - 3)}}{3}\)
\( = \frac{{3{x^2} - 12x + 9}}{3}\)
\( = {x^2} - 4x + 3 = (x - 3)(x - 1)\)
Xét \(y' = 0\) \( \Rightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\)
Ta có bảng biến thiên:
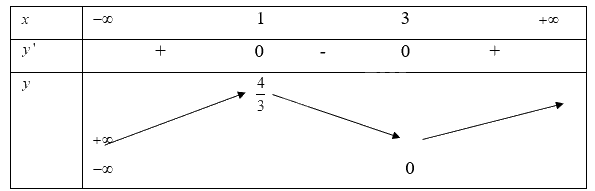
Từ bảng biến thiên ta có
Hàm số đạt giá trị cực đại tại \(x = 1\)khi đó\(y = \frac{4}{3}\)
Hàm số đạt giá trị cực tiểu tại \(x = 3\)khi đó \(y = 0\)
b) \(y = \left| x \right|\)
Hàm số trên xác định trên R
\(y = \left| x \right|\)\( = \sqrt {{x^2}} \)
Ta có: \(y' = \frac{{2x}}{{2\sqrt {{x^2}} }} = \frac{x}{{\sqrt {{x^2}} }}\)
Vì \(\sqrt {{x^2}} > 0\)nên dấu của \(y'\)cũng là dấu của \(x\)
Khi đó ta có bảng biến thiên
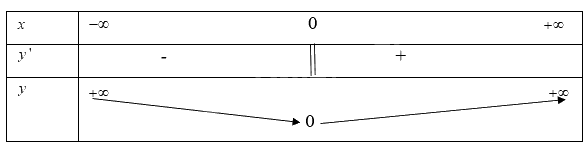
Từ bảng biến thiên ta có
Hàm số trên đạt giá trị cực tiểu tại \(x = 0\) khi đó \(y = 0\)
c) \(y = {3^{x - 2{x^2}}}\)
Hàm số trên xác định trên R
Ta có: \(y' = {3^{x - 2{x^2}}}(1 - 4x)\)
Xét \(y' = 0\)\( \Rightarrow 1 - 4x = 0\) \( \Rightarrow x = \frac{1}{4}\)
Ta có bảng biến thiên
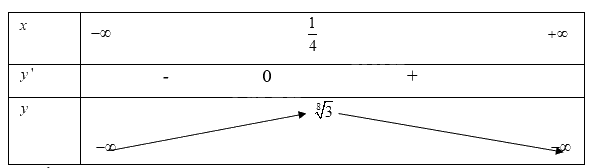
Từ bảng biến thiên ta có
Hàm số trên đạt giá trị cực tiểu tại\(x = \frac{1}{4}\)khi đó \(y = \sqrt[8]{3}\)
d) \(y = \ln ({x^2} + e)\)
Hàm số trên xác định trên R
Ta có: \(y' = \frac{{2x}}{{{x^2} + e}}\)
Xét \(y' = 0\)\( \Rightarrow x = 0\)
Ta có bảng biến thiên
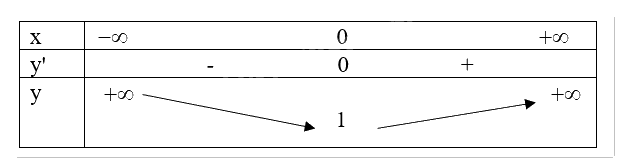
Từ bảng biến thiên ta có:
Hàm số trên đạt giá trị cực tiểu tại \(x = 0\)khi đó \(y = 1\)
Bài tập 1.3 trang 9 SGK Toán 12 tập 1 thuộc chương trình học môn Toán lớp 12, tập trung vào việc ôn tập các kiến thức về hàm số bậc hai và ứng dụng của chúng. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập 1.3 bao gồm một số câu hỏi trắc nghiệm và bài tập tự luận, yêu cầu học sinh:
Để giải bài tập 1.3 trang 9 SGK Toán 12 tập 1 một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Bài 1: Cho hàm số y = x2 - 4x + 3. Tìm tọa độ đỉnh của parabol.
Giải:
Hệ số a = 1, b = -4, c = 3.
x0 = -b/2a = -(-4)/(2*1) = 2.
y0 = -Δ/4a = -( (-4)2 - 4*1*3 ) / (4*1) = -(16 - 12) / 4 = -1.
Vậy tọa độ đỉnh của parabol là I(2, -1).
Ngoài SGK Toán 12 tập 1, học sinh có thể tham khảo thêm các tài liệu sau:
Bài tập 1.3 trang 9 SGK Toán 12 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!