Chào mừng các em học sinh đến với bài giải chi tiết bài tập 2.23 trang 80 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến kiến thức đã học.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Trong Hoá học, cấu tạo của phân tử amoniac (\(N{H_3}\)) có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen (\(N\)) và đáy là tam giác \({H_1}{H_2}{H_3}\) với \({H_1}\), \({H_2}\), \({H_3}\) là vị trí của ba nguyên tử hydrogen (\(H\)). Góc tạo bởi liên kết \(H - N - H\), có hai cạnh là hai đoạn thẳng nối \(N\) với hai trong ba điểm \({H_1}\), \({H_2}\), \({H_3}\) (chẳng hạn như \({H_1}N{H_2}\)), được gọi là góc liên kết của phân tử \(N{H_3}\). Góc này xấp xỉ \({107^\circ }\). Trong khô
Đề bài
Trong Hoá học, cấu tạo của phân tử amoniac (\(N{H_3}\)) có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen (\(N\)) và đáy là tam giác \({H_1}{H_2}{H_3}\) với \({H_1}\), \({H_2}\), \({H_3}\) là vị trí của ba nguyên tử hydrogen (\(H\)). Góc tạo bởi liên kết \(H - N - H\), có hai cạnh là hai đoạn thẳng nối \(N\) với hai trong ba điểm \({H_1}\), \({H_2}\), \({H_3}\) (chẳng hạn như \({H_1}N{H_2}\)), được gọi là góc liên kết của phân tử \(N{H_3}\). Góc này xấp xỉ \({107^\circ }\).
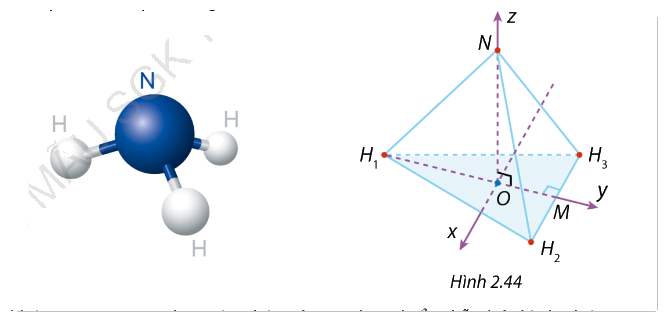
Trong không gian Oxyz, cho một phân tử \(N{H_3}\) được biểu diễn bởi hình chóp tam giác đều \(N.{H_1}{H_2}{H_3}\) với \(O\) là tâm của đáy. Nguyên tử nitrogen được biểu diễn bởi điểm \(N\) thuộc trục Oz, ba nguyên tử hydrogen ở các vị trí \({H_1}\), \({H_2}\), \({H_3}\) trong đó \({H_1}(0; - 2;0)\) và \({H_2}{H_3}\) song song với trục Ox (Hình 2.44).
a) Tính khoảng cách giữa hai nguyên tử hydrogen.
b) Tính khoảng cách giữa nguyên tử nitrogen với mỗi nguyên tử hydrogen (làm tròn các kết quả tính toán đến hàng phần trăm).
Phương pháp giải - Xem chi tiết
a) Sử dụng định lý sin trong công thức để tính khoảng cách giữa hai nguyên tử hydrogen (d) có góc bằng ∝.
\(d = 2R.\sin (\alpha )\)
b) Sử dụng công thức tính khoảng cách giữa hai điểm trong không gian:
\(d(N,{H_1}) = \sqrt {{{({x_{{H_1}}} - {x_N})}^2} + {{({y_{{H_1}}} - {y_N})}^2} + {{({z_{{H_1}}} - {z_N})}^2}} \)
Thay các tọa độ tương ứng để tính khoảng cách \(d(N,{H_1})\), \(d(N,{H_2})\), \(d(N,{H_3})\).
Lời giải chi tiết
a)
Bởi vì tam giác \({H_1}{H_2}{H_3}\) là tam giác đều nên áp dụng vào định lý sin trong tam giác, ta có:
\({H_1}{H_2} = {H_1}{H_3} = {H_2}{H_3} = 2R\sin {60^\circ } = \sqrt 3 R\)
Trong trường hợp này, O là trọng tâm của tam giác \({H_1}{H_2}{H_3}\) và O cũng là bán kính đường tròn ngoại tiếp nên \(R = 2\), ta có: \(d = 2\sqrt 3 \)
b) Để tính khoảng cách giữa nguyên tử nitrogen \(N(0;0;z)\) với nguyên tử hydrogen \({H_1}(0; - 2;0)\), ta sử dụng công thức:
\(N{H_1} = \sqrt {{{(0 - 0)}^2} + {{(0 + 2)}^2} + {{(z - 0)}^2}} = \sqrt {4 + {z^2}} \)
Vì khoảng cách từ gốc toạ độ O đến \({H_2}\) là 2, do đó \({H_2}\) có toạ độ là
\({H_2}(2\cos \theta ;2\sin \theta ;0)\)
Với θ là góc \(\widehat {xO{H_2}}\). Và vì \({H_1}{H_2}{H_3}\) là tam giác đều nên \(\widehat {xO{H_2}} = 30^\circ \).
Vậy \({H_2}\) có toạ độ là: \({H_2}(\sqrt 3 ;1;0)\)
Toạ độ của vectơ \(\overrightarrow {N{H_1}} ,\overrightarrow {N{H_2}} \)là:
\(\overrightarrow {N{H_1}} = \left( {0; - 2; - z} \right),\overrightarrow {N{H_2}} = \left( {\sqrt 3 ;1; - z} \right)\)
Từ đó ta có \(z\): \(\cos {107^\circ } = \frac{{\overrightarrow {N{H_1}} .\overrightarrow {N{H_2}} }}{{\left| {\overrightarrow {N{H_1}} } \right|.\left| {\overrightarrow {N{H_2}} } \right|}} = \frac{{ - 2 + {z^2}}}{{4 + {z^2}}}\)
Suy ra: \( - 2 + {z^2} = \left( {4 + {z^2}} \right).\cos 107^\circ \Leftrightarrow 0,71{z^2} = 0,83 \Rightarrow z = 1,08\).
Bài tập 2.23 trang 80 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về đường thẳng và mặt phẳng trong không gian. Để giải bài tập này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hai đường thẳng d1 và d2. Tìm giao điểm của hai đường thẳng này.)
Lời giải:
Để tìm giao điểm của hai đường thẳng d1 và d2, ta cần giải hệ phương trình:
(Phương trình của d1)
(Phương trình của d2)
Giải hệ phương trình này, ta tìm được tọa độ giao điểm (x, y, z). Nếu hệ phương trình vô nghiệm, thì hai đường thẳng không có giao điểm.
Ngoài bài tập 2.23, còn rất nhiều bài tập tương tự liên quan đến đường thẳng và mặt phẳng trong không gian. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Kiến thức về đường thẳng và mặt phẳng trong không gian có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như:
Để nắm vững kiến thức về đường thẳng và mặt phẳng trong không gian, các em nên luyện tập thêm nhiều bài tập khác nhau. Các em có thể tìm thấy các bài tập này trong SGK Toán 12 tập 1, các sách bài tập Toán 12, hoặc trên các trang web học toán online như giaitoan.edu.vn.
Bài tập 2.23 trang 80 SGK Toán 12 tập 1 là một bài toán quan trọng, giúp các em rèn luyện kỹ năng giải các bài toán liên quan đến đường thẳng và mặt phẳng trong không gian. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày ở trên, các em sẽ tự tin hơn khi làm bài tập Toán 12.