Chào mừng các em học sinh đến với bài giải chi tiết bài tập 1.44 trang 48 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học Toán 12 tập 1, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
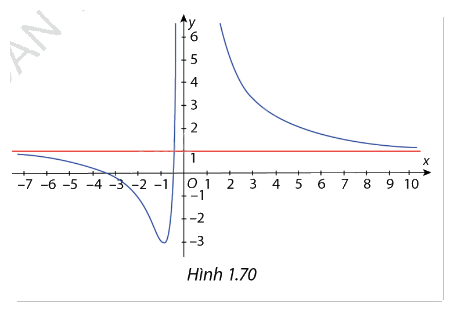
Cho hàm số \(y = \frac{{{x^2} + 7x + 3}}{{{x^2}}}\) có đồ thị là đường cong như Hình 1.70. Đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận? A. 1 . B. 2 . C. 3 . D. 4 .
Đề bài
Cho hàm số \(y = \frac{{{x^2} + 7x + 3}}{{{x^2}}}\) có đồ thị là đường cong như Hình 1.70. Đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận?
A. 1
B. 2
C. 3
D. 4
Phương pháp giải - Xem chi tiết
Khái niệm: Đường tiệm cận của một hàm số là một đường thẳng mà đồ thị của hàm số tiến đến càng gần khi giá trị của biến số tiến ra vô cùng hoặc tiến tới một điểm đặc biệt nào đó nhưng không bao giờ chạm vào đường thẳng đó.
Lời giải chi tiết
Nhìn vào đồ thị có thể thấy đồ thị hàm số có 1 tiệm cận ngang là \(y = 1\).
Ngoài ra đồ thị còn 1 tiệm cận đứng đó là \(x = 0\)
Vậy đồ thị hàm số có 2 đường tiệm cận. Chọn B.
Bài tập 1.44 trang 48 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học về đạo hàm. Bài toán này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán liên quan đến tính đơn điệu của hàm số, cực trị của hàm số và ứng dụng của đạo hàm trong việc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
Bài tập 1.44 thường có dạng như sau: Cho hàm số y = f(x). Tìm các điểm cực trị của hàm số. Xác định khoảng đồng biến, nghịch biến của hàm số. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
Giải:
Hy vọng với bài giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải bài tập 1.44 trang 48 SGK Toán 12 tập 1. Chúc các em học tập tốt!