Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 47, 48, 49 SGK Toán 12 tập 2 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin làm bài tập.
Bài học này thuộc chương trình Toán 12 tập 2, tập trung vào các kiến thức về tích phân và ứng dụng của tích phân.
Trong không gian \(Oxyz\), cho hai mặt phẳng \(\left( {{\alpha _1}} \right):2x - 3y + z + 3 = 0\), \(\left( {{\alpha _2}} \right):4x - 6y + 2z + 5 = 0\)và điểm \(M( - 2;0;1)\). a) Hãy chỉ ra một vectơ pháp tuyến của mỗi mặt phẳng. Có nhận xét gì về phương của các vectơ này? b) Mặt phẳng nào đi qua điểm M? c) Hai mặt phẳng này song song với nhau không? Vì sao?
Trả lời câu hỏi Luyện tập 7 trang 48 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho hình lăng trụ \(ABC.A'B'C'\) với các điểm \(A'(3;2; - 5)\), \(A(3;1; - 1)\), \(B(2; - 1;4)\), và \(C(0;2;1)\).
a) Chứng minh rằng mặt phẳng (ABC) song song với mặt phẳng \(\alpha \): \(9x + 13y + 7z = 0\)
b) Viết phương trình mặt phẳng (A'B'C').
Phương pháp giải:
a)
- Tìm vectơ pháp tuyến của mặt phẳng (ABC).
- Sử dụng tính chất: Hai mặt phẳng song song khi và chỉ khi các vector pháp tuyến của chúng cùng phương, nghĩa là tỉ số các hệ số của hai phương trình mặt phẳng phải tương ứng với nhau.
b)
- Vectơ pháp tuyến của mặt phẳng A′B′C′ cũng là vectơ pháp tuyến của mặt phẳng ABC vì hai mặt phẳng này song song.
- Sau đó viết phương trình mặt phẳng dựa vào vectơ pháp tuyến này và tọa độ của một điểm trên mặt phẳng, ví dụ A′.
Lời giải chi tiết:
a)
Tọa độ các điểm \(A(3;1; - 1)\), \(B(2; - 1;4)\), \(C(0;2;1)\).
Vector \(\overrightarrow {AB} = B - A = (2 - 3, - 1 - 1,4 - ( - 1)) = ( - 1, - 2,5)\).
Vector \(\overrightarrow {AC} = C - A = (0 - 3,2 - 1,1 - ( - 1)) = ( - 3,1,2)\).
Tích có hướng của \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) là:
\(\overrightarrow {{n_{ABC}}} = \overrightarrow {AB} \times \overrightarrow {AC} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\{ - 1}&{ - 2}&5\\{ - 3}&1&2\end{array}} \right| = {\bf{i}} \cdot (( - 2) \cdot 2 - 5 \cdot 1) - {\bf{j}} \cdot (( - 1) \cdot 2 - 5 \cdot ( - 3)) + {\bf{k}} \cdot (( - 1) \cdot 1 - ( - 2) \cdot ( - 3))\)
\( = {\bf{i}} \cdot ( - 4 - 5) - {\bf{j}} \cdot ( - 2 + 15) + {\bf{k}} \cdot ( - 1 - 6) = {\bf{i}} \cdot ( - 9) - {\bf{j}} \cdot (13) + {\bf{k}} \cdot ( - 7) = ( - 9, - 13, - 7).\)
Vậy vector pháp tuyến của mặt phẳng (ABC) là \(\overrightarrow {{n_{ABC}}} = ( - 9, - 13, - 7)\).
Phương trình mặt phẳng \(\alpha \) cho trước là: \(9x + 13y + 7z = 0\).
Vector pháp tuyến của mặt phẳng \(\alpha \) là \(\overrightarrow {{n_\alpha }} = (9,13,7)\).
Ta thấy \(\overrightarrow {{n_{ABC}}} = ( - 9, - 13, - 7)\) là cùng phương với \(\overrightarrow {{n_\alpha }} \), do đó hai mặt phẳng (ABC) và \(\alpha \) song song với nhau.
b)
Vì \(ABC.A'B'C'\) là hình lăng trụ nên mặt phẳng ABC và mặt phẳng A′B′C′ song song với nhau nên vectơ pháp tuyến của mặt phẳng ABC cũng là vectơ pháp tuyến của mặt phẳng A′B′C′.
Suy ra vector pháp tuyến của mặt phẳng A′B′C′ là \(\overrightarrow {{n_{A'B'C'}}} = ( - 9, - 13, - 7)\).
Phương trình mặt phẳng (A'B'C') là:
\( - 9(x - 3) - 13(y - 2) - 7(z + 5) = 0\)
hay rút gọn lại là:
\( - 9x - 13y - 7z + 18 = 0\)
Trả lời câu hỏi Hoạt động 6 trang 47 SGK Toán 12 Cùng khám phá
Trong không gian \(Oxyz\), cho hai mặt phẳng \(\left( {{\alpha _1}} \right):2x - 3y + z + 3 = 0\), \(\left( {{\alpha _2}} \right):4x - 6y + 2z + 5 = 0\)và điểm \(M( - 2;0;1)\).
a) Hãy chỉ ra một vectơ pháp tuyến của mỗi mặt phẳng. Có nhận xét gì về phương của các vectơ này?
b) Mặt phẳng nào đi qua điểm M?
c) Hai mặt phẳng này song song với nhau không? Vì sao?
Phương pháp giải:
a) Phương trình mặt phẳng có dạng \(Ax + By + Cz + D = 0\) thì \(\overrightarrow n = \left( {A;B;C} \right)\) chính là vectơ pháp tuyến của mặt phẳng đó.
b) Thay \(M\) vào từng phương trình của mặt phẳng để kiểm tra.
c) Nếu vectơ pháp tuyến của hai mặt phẳng song song hoặc trùng nhau thì hai mặt phẳng đó cũng song song hoặc trùng nhau.
Lời giải chi tiết:
a)
Vectơ pháp tuyến của hai mặt phẳng là:
\(\overrightarrow {{n_{{\alpha _1}}}} = \left( {2; - 3;1} \right)\), \(\overrightarrow {{n_{{\alpha _2}}}} = \left( {4; - 6;2} \right)\)
Có thể thấy hai vectơ này cùng phương với nhau vì:
\(\frac{4}{2} = \frac{{ - 6}}{{ - 3}} = \frac{2}{1} = 2\)
b)
Thay M vào phương trình mặt phẳng \(({\alpha _1})\):
\(2.( - 2) - 3.0 + 1 + 3 = 0\)
Thay M vào phương trình mặt phẳng \(({\alpha _2})\):
\(4.( - 2) - 6.0 + 2.1 + 5 = - 1 \ne 0\)
Vậy M thuộc mặt phẳng \(({\alpha _1})\) nhưng không thuộc mặt phẳng \(({\alpha _2})\).
c)
Từ câu a có thể thấy hai vectơ pháp tuyến \(\overrightarrow {{n_{{\alpha _1}}}} ,\overrightarrow {{n_{{\alpha _2}}}} \) song song với nhau nên hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) có thể song song hoặc trùng nhau.
Mặt khác, điểm M thuộc mặt phẳng \(({\alpha _1})\) nhưng không thuộc mặt phẳng \(({\alpha _2})\) nên hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) song song với nhau.
Trả lời câu hỏi Luyện tập 8 trang 49 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho hình chóp S.ABC có \(S(2; - 1;7)\), \(A(2; - 1;3)\), \(B(5;2;3)\), \(C(8; - 1;3)\). Chứng minh rằng mặt phẳng (SAB) vuông góc với hai mặt phẳng (ABC) và (SBC).
Phương pháp giải:
Để chứng minh mặt phẳng \((SAB)\) vuông góc với mặt phẳng \((ABC)\), ta cần kiểm tra xem tích vô hướng của hai vectơ pháp tuyến của hai mặt phẳng này có bằng 0 hay không. - Tương tự, để chứng minh mặt phẳng \((SAB)\) vuông góc với mặt phẳng \((SBC)\), ta cũng kiểm tra điều kiện tích vô hướng giữa hai vectơ pháp tuyến của chúng.
Lời giải chi tiết:
* Tìm vectơ pháp tuyến của các mặt phẳng
a) Mặt phẳng \((ABC)\):
- Ta cần tìm hai vectơ chỉ phương của mặt phẳng \((ABC)\):
\(\overrightarrow {AB} = B - A = (5 - 2;2 + 1;3 - 3) = (3;3;0),\)
\(\overrightarrow {AC} = C - A = (8 - 2; - 1 + 1;3 - 3) = (6;0;0).\)
- Vectơ pháp tuyến của mặt phẳng \((ABC)\) là tích có hướng của \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
\(\overrightarrow {{n_{ABC}}} = \overrightarrow {AB} \times \overrightarrow {AC} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\3&3&0\\6&0&0\end{array}} \right| = (0;0; - 18).\)
Do đó, một vectơ pháp tuyến của mặt phẳng \((ABC)\) là \(\overrightarrow {{n_{ABC}}} = (0;0; - 18)\).
b) Mặt phẳng \((SAB)\):
- Ta cần tìm hai vectơ chỉ phương của mặt phẳng \((SAB)\):
\(\overrightarrow {SA} = A - S = (2 - 2; - 1 + 1;3 - 7) = (0;0; - 4),\)
\(\overrightarrow {SB} = B - S = (5 - 2;2 + 1;3 - 7) = (3;3; - 4).\)
- Vectơ pháp tuyến của mặt phẳng \((SAB)\) là tích có hướng của \(\overrightarrow {SA} \) và \(\overrightarrow {SB} \):
\(\overrightarrow {{n_{SAB}}} = \overrightarrow {SA} \times \overrightarrow {SB} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\0&0&{ - 4}\\3&3&{ - 4}\end{array}} \right| = (12; - 12;0).\)
Do đó, một vectơ pháp tuyến của mặt phẳng \((SAB)\) là \(\overrightarrow {{n_{SAB}}} = (12; - 12;0)\).
c) Mặt phẳng \((SBC)\):
- Tương tự, ta cần tìm hai vectơ chỉ phương của mặt phẳng \((SBC)\):
\(\overrightarrow {SB} = (3;3; - 4)\quad {\rm{v\`a }}\quad \overrightarrow {SC} = C - S = (8 - 2; - 1 + 1;3 - 7) = (6;0; - 4).\)
- Vectơ pháp tuyến của mặt phẳng \((SBC)\) là tích có hướng của \(\overrightarrow {SB} \) và \(\overrightarrow {SC} \):
\(\overrightarrow {{n_{SBC}}} = \overrightarrow {SB} \times \overrightarrow {SC} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\3&3&{ - 4}\\6&0&{ - 4}\end{array}} \right| = ( - 12; - 12; - 18).\)
Do đó, một vectơ pháp tuyến của mặt phẳng \((SBC)\) là:
\(\overrightarrow {{n_{SBC}}} = ( - 12; - 12; - 18)\)
* Chứng minh các mặt phẳng vuông góc
a) Mặt phẳng \((SAB)\) và \((ABC)\):
- Để kiểm tra \((SAB)\) vuông góc với \((ABC)\), ta tính tích vô hướng của \(\overrightarrow {{n_{SAB}}} \) và \(\overrightarrow {{n_{ABC}}} \):
\(\overrightarrow {{n_{SAB}}} \cdot \overrightarrow {{n_{ABC}}} = (12; - 12;0) \cdot (0;0; - 18) = 12 \times 0 + ( - 12) \times 0 + 0 \times ( - 18) = 0.\)
- Vì tích vô hướng bằng 0, nên \((SAB) \bot (ABC)\).
b) Mặt phẳng \((SAB)\) và \((SBC)\):
- Tương tự, ta tính tích vô hướng của \(\overrightarrow {{n_{SAB}}} \) và \(\overrightarrow {{n_{SBC}}} \):
\(\overrightarrow {{n_{SAB}}} \cdot \overrightarrow {{n_{SBC}}} = (12; - 12;0) \cdot ( - 12; - 12; - 18) = 12 \times ( - 12) + ( - 12) \times ( - 12) + 0 \times ( - 18) = - 144 + 144 + 0 = 0.\)
- Vì tích vô hướng bằng 0, nên \((SAB) \bot (SBC)\).
Trả lời câu hỏi Luyện tập 9 trang 49 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, viết phương trình mặt phẳng \((\alpha )\) đi qua \(A( - 3;2; - 1)\) và vuông góc với hai mặt phẳng \((P):2x - y + 3z - 1 = 0\), \((Q):x + 2y - 2z + 3 = 0\).
Phương pháp giải:
- Vectơ pháp tuyến của mặt phẳng \((\alpha )\) phải vuông góc với cả hai vectơ pháp tuyến của các mặt phẳng \((P)\) và \((Q)\).
- Từ đó, ta tìm vectơ pháp tuyến của \((\alpha )\) bằng tích có hướng của hai vectơ pháp tuyến của \((P)\) và \((Q)\).
- Sau khi có vectơ pháp tuyến của \((\alpha )\), sử dụng điểm \(A( - 3;2; - 1)\) để lập phương trình mặt phẳng \((\alpha )\).
Lời giải chi tiết:
- Vectơ pháp tuyến của mặt phẳng \((P)\) là:
\(\overrightarrow {{n_P}} = (2; - 1;3).\)
- Vectơ pháp tuyến của mặt phẳng \((Q)\) là:
\(\overrightarrow {{n_Q}} = (1;2; - 2).\)
- Vectơ pháp tuyến của mặt phẳng \((\alpha )\) phải vuông góc với cả hai vectơ \(\overrightarrow {{n_P}} \) và \(\overrightarrow {{n_Q}} \), do đó ta tìm tích có hướng của hai vectơ này:
\(\overrightarrow {{n_\alpha }} = \overrightarrow {{n_P}} \times \overrightarrow {{n_Q}} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\2&{ - 1}&3\\1&2&{ - 2}\end{array}} \right| = {\bf{i}}\left| {\begin{array}{*{20}{c}}{ - 1}&3\\2&{ - 2}\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}2&3\\1&{ - 2}\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}2&{ - 1}\\1&2\end{array}} \right|\)
Tính các định thức con:
\(\overrightarrow {{n_\alpha }} = {\bf{i}} \cdot (( - 1)( - 2) - (3)(2)) - {\bf{j}} \cdot ((2)( - 2) - (3)(1)) + {\bf{k}} \cdot ((2)(2) - ( - 1)(1))\)
\( = {\bf{i}} \cdot (2 - 6) - {\bf{j}} \cdot ( - 4 - 3) + {\bf{k}} \cdot (4 + 1)\)
\( = {\bf{i}} \cdot ( - 4) - {\bf{j}} \cdot ( - 7) + {\bf{k}} \cdot (5)\)
\( = ( - 4;7;5).\)
Vậy vectơ pháp tuyến của mặt phẳng \((\alpha )\) là \(\overrightarrow {{n_\alpha }} = ( - 4;7;5)\).
- Phương trình tổng quát của mặt phẳng \((\alpha )\) có dạng:
\( - 4(x + 3) + 7(y - 2) + 5(z + 1) = 0.\)
- Ta thế tọa độ điểm \(A( - 3;2; - 1)\) vào phương trình:
\( - 4(x + 3) + 7(y - 2) + 5(z + 1) = 0.\)
Mở rộng phương trình:
\( - 4x - 12 + 7y - 14 + 5z + 5 = 0\)
\( - 4x + 7y + 5z - 21 = 0.\)
Vậy phương trình của mặt phẳng \((\alpha )\) là:
\( - 4x + 7y + 5z - 21 = 0.\)
Trả lời câu hỏi Hoạt động 7 trang 48 SGK Toán 12 Cùng khám phá
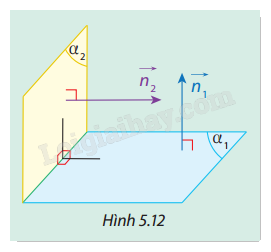
Cho hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) có vectơ pháp tuyến tương ứng là \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) (Hình 5.12).
a) Có nhận xét gì về góc giữa \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) khi \(({\alpha _1}) \bot ({\alpha _2})\)?
b) Nếu \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) vuông góc với nhau thì \(({\alpha _1})\) và \(({\alpha _2})\) có vuông góc với nhau không? Vì sao?
Phương pháp giải:
a) Góc giữa hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) cũng là góc giữa hai vectơ \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).
b) Tương tự thì góc góc giữa hai vectơ \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) cũng là góc giữa hai mặt phẳng \(({\alpha _1})\) và.
Lời giải chi tiết:
a)
Khi hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) vuông góc, điều này có nghĩa rằng góc giữa hai mặt phẳng bằng \({90^\circ }\).
Do đó, vectơ pháp tuyến \(\overrightarrow {{n_1}} \) của mặt phẳng \(({\alpha _1})\) và vectơ pháp tuyến \(\overrightarrow {{n_2}} \) của mặt phẳng \(({\alpha _2})\) cũng sẽ vuông góc với nhau.
Điều này được biểu diễn bằng tích vô hướng của hai vectơ \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \):
\(\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} = 0.\)
Kết luận: Khi \(({\alpha _1}) \bot ({\alpha _2})\), thì \(\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \).
b)
Nếu \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) vuông góc với nhau, tức là \(\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} = 0\), thì hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) cũng sẽ vuông góc với nhau vì:
\(\left( {{\alpha _1}} \right) \bot \overrightarrow {{n_1}} ,\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \to \left( {{\alpha _1}} \right)//\overrightarrow {{n_2}} \)
Mà
\(\left( {{\alpha _2}} \right) \bot \overrightarrow {{n_2}} \to \left( {{\alpha _1}} \right) \bot \left( {{\alpha _2}} \right)\).
Trả lời câu hỏi Hoạt động 6 trang 47 SGK Toán 12 Cùng khám phá
Trong không gian \(Oxyz\), cho hai mặt phẳng \(\left( {{\alpha _1}} \right):2x - 3y + z + 3 = 0\), \(\left( {{\alpha _2}} \right):4x - 6y + 2z + 5 = 0\)và điểm \(M( - 2;0;1)\).
a) Hãy chỉ ra một vectơ pháp tuyến của mỗi mặt phẳng. Có nhận xét gì về phương của các vectơ này?
b) Mặt phẳng nào đi qua điểm M?
c) Hai mặt phẳng này song song với nhau không? Vì sao?
Phương pháp giải:
a) Phương trình mặt phẳng có dạng \(Ax + By + Cz + D = 0\) thì \(\overrightarrow n = \left( {A;B;C} \right)\) chính là vectơ pháp tuyến của mặt phẳng đó.
b) Thay \(M\) vào từng phương trình của mặt phẳng để kiểm tra.
c) Nếu vectơ pháp tuyến của hai mặt phẳng song song hoặc trùng nhau thì hai mặt phẳng đó cũng song song hoặc trùng nhau.
Lời giải chi tiết:
a)
Vectơ pháp tuyến của hai mặt phẳng là:
\(\overrightarrow {{n_{{\alpha _1}}}} = \left( {2; - 3;1} \right)\), \(\overrightarrow {{n_{{\alpha _2}}}} = \left( {4; - 6;2} \right)\)
Có thể thấy hai vectơ này cùng phương với nhau vì:
\(\frac{4}{2} = \frac{{ - 6}}{{ - 3}} = \frac{2}{1} = 2\)
b)
Thay M vào phương trình mặt phẳng \(({\alpha _1})\):
\(2.( - 2) - 3.0 + 1 + 3 = 0\)
Thay M vào phương trình mặt phẳng \(({\alpha _2})\):
\(4.( - 2) - 6.0 + 2.1 + 5 = - 1 \ne 0\)
Vậy M thuộc mặt phẳng \(({\alpha _1})\) nhưng không thuộc mặt phẳng \(({\alpha _2})\).
c)
Từ câu a có thể thấy hai vectơ pháp tuyến \(\overrightarrow {{n_{{\alpha _1}}}} ,\overrightarrow {{n_{{\alpha _2}}}} \) song song với nhau nên hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) có thể song song hoặc trùng nhau.
Mặt khác, điểm M thuộc mặt phẳng \(({\alpha _1})\) nhưng không thuộc mặt phẳng \(({\alpha _2})\) nên hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) song song với nhau.
Trả lời câu hỏi Luyện tập 7 trang 48 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho hình lăng trụ \(ABC.A'B'C'\) với các điểm \(A'(3;2; - 5)\), \(A(3;1; - 1)\), \(B(2; - 1;4)\), và \(C(0;2;1)\).
a) Chứng minh rằng mặt phẳng (ABC) song song với mặt phẳng \(\alpha \): \(9x + 13y + 7z = 0\)
b) Viết phương trình mặt phẳng (A'B'C').
Phương pháp giải:
a)
- Tìm vectơ pháp tuyến của mặt phẳng (ABC).
- Sử dụng tính chất: Hai mặt phẳng song song khi và chỉ khi các vector pháp tuyến của chúng cùng phương, nghĩa là tỉ số các hệ số của hai phương trình mặt phẳng phải tương ứng với nhau.
b)
- Vectơ pháp tuyến của mặt phẳng A′B′C′ cũng là vectơ pháp tuyến của mặt phẳng ABC vì hai mặt phẳng này song song.
- Sau đó viết phương trình mặt phẳng dựa vào vectơ pháp tuyến này và tọa độ của một điểm trên mặt phẳng, ví dụ A′.
Lời giải chi tiết:
a)
Tọa độ các điểm \(A(3;1; - 1)\), \(B(2; - 1;4)\), \(C(0;2;1)\).
Vector \(\overrightarrow {AB} = B - A = (2 - 3, - 1 - 1,4 - ( - 1)) = ( - 1, - 2,5)\).
Vector \(\overrightarrow {AC} = C - A = (0 - 3,2 - 1,1 - ( - 1)) = ( - 3,1,2)\).
Tích có hướng của \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) là:
\(\overrightarrow {{n_{ABC}}} = \overrightarrow {AB} \times \overrightarrow {AC} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\{ - 1}&{ - 2}&5\\{ - 3}&1&2\end{array}} \right| = {\bf{i}} \cdot (( - 2) \cdot 2 - 5 \cdot 1) - {\bf{j}} \cdot (( - 1) \cdot 2 - 5 \cdot ( - 3)) + {\bf{k}} \cdot (( - 1) \cdot 1 - ( - 2) \cdot ( - 3))\)
\( = {\bf{i}} \cdot ( - 4 - 5) - {\bf{j}} \cdot ( - 2 + 15) + {\bf{k}} \cdot ( - 1 - 6) = {\bf{i}} \cdot ( - 9) - {\bf{j}} \cdot (13) + {\bf{k}} \cdot ( - 7) = ( - 9, - 13, - 7).\)
Vậy vector pháp tuyến của mặt phẳng (ABC) là \(\overrightarrow {{n_{ABC}}} = ( - 9, - 13, - 7)\).
Phương trình mặt phẳng \(\alpha \) cho trước là: \(9x + 13y + 7z = 0\).
Vector pháp tuyến của mặt phẳng \(\alpha \) là \(\overrightarrow {{n_\alpha }} = (9,13,7)\).
Ta thấy \(\overrightarrow {{n_{ABC}}} = ( - 9, - 13, - 7)\) là cùng phương với \(\overrightarrow {{n_\alpha }} \), do đó hai mặt phẳng (ABC) và \(\alpha \) song song với nhau.
b)
Vì \(ABC.A'B'C'\) là hình lăng trụ nên mặt phẳng ABC và mặt phẳng A′B′C′ song song với nhau nên vectơ pháp tuyến của mặt phẳng ABC cũng là vectơ pháp tuyến của mặt phẳng A′B′C′.
Suy ra vector pháp tuyến của mặt phẳng A′B′C′ là \(\overrightarrow {{n_{A'B'C'}}} = ( - 9, - 13, - 7)\).
Phương trình mặt phẳng (A'B'C') là:
\( - 9(x - 3) - 13(y - 2) - 7(z + 5) = 0\)
hay rút gọn lại là:
\( - 9x - 13y - 7z + 18 = 0\)
Trả lời câu hỏi Hoạt động 7 trang 48 SGK Toán 12 Cùng khám phá
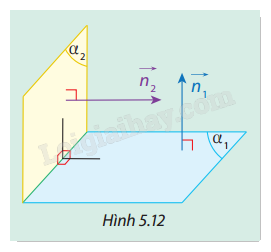
Cho hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) có vectơ pháp tuyến tương ứng là \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) (Hình 5.12).
a) Có nhận xét gì về góc giữa \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) khi \(({\alpha _1}) \bot ({\alpha _2})\)?
b) Nếu \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) vuông góc với nhau thì \(({\alpha _1})\) và \(({\alpha _2})\) có vuông góc với nhau không? Vì sao?
Phương pháp giải:
a) Góc giữa hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) cũng là góc giữa hai vectơ \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).
b) Tương tự thì góc góc giữa hai vectơ \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) cũng là góc giữa hai mặt phẳng \(({\alpha _1})\) và.
Lời giải chi tiết:
a)
Khi hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) vuông góc, điều này có nghĩa rằng góc giữa hai mặt phẳng bằng \({90^\circ }\).
Do đó, vectơ pháp tuyến \(\overrightarrow {{n_1}} \) của mặt phẳng \(({\alpha _1})\) và vectơ pháp tuyến \(\overrightarrow {{n_2}} \) của mặt phẳng \(({\alpha _2})\) cũng sẽ vuông góc với nhau.
Điều này được biểu diễn bằng tích vô hướng của hai vectơ \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \):
\(\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} = 0.\)
Kết luận: Khi \(({\alpha _1}) \bot ({\alpha _2})\), thì \(\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \).
b)
Nếu \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) vuông góc với nhau, tức là \(\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} = 0\), thì hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) cũng sẽ vuông góc với nhau vì:
\(\left( {{\alpha _1}} \right) \bot \overrightarrow {{n_1}} ,\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \to \left( {{\alpha _1}} \right)//\overrightarrow {{n_2}} \)
Mà
\(\left( {{\alpha _2}} \right) \bot \overrightarrow {{n_2}} \to \left( {{\alpha _1}} \right) \bot \left( {{\alpha _2}} \right)\).
Trả lời câu hỏi Luyện tập 8 trang 49 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho hình chóp S.ABC có \(S(2; - 1;7)\), \(A(2; - 1;3)\), \(B(5;2;3)\), \(C(8; - 1;3)\). Chứng minh rằng mặt phẳng (SAB) vuông góc với hai mặt phẳng (ABC) và (SBC).
Phương pháp giải:
Để chứng minh mặt phẳng \((SAB)\) vuông góc với mặt phẳng \((ABC)\), ta cần kiểm tra xem tích vô hướng của hai vectơ pháp tuyến của hai mặt phẳng này có bằng 0 hay không. - Tương tự, để chứng minh mặt phẳng \((SAB)\) vuông góc với mặt phẳng \((SBC)\), ta cũng kiểm tra điều kiện tích vô hướng giữa hai vectơ pháp tuyến của chúng.
Lời giải chi tiết:
* Tìm vectơ pháp tuyến của các mặt phẳng
a) Mặt phẳng \((ABC)\):
- Ta cần tìm hai vectơ chỉ phương của mặt phẳng \((ABC)\):
\(\overrightarrow {AB} = B - A = (5 - 2;2 + 1;3 - 3) = (3;3;0),\)
\(\overrightarrow {AC} = C - A = (8 - 2; - 1 + 1;3 - 3) = (6;0;0).\)
- Vectơ pháp tuyến của mặt phẳng \((ABC)\) là tích có hướng của \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
\(\overrightarrow {{n_{ABC}}} = \overrightarrow {AB} \times \overrightarrow {AC} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\3&3&0\\6&0&0\end{array}} \right| = (0;0; - 18).\)
Do đó, một vectơ pháp tuyến của mặt phẳng \((ABC)\) là \(\overrightarrow {{n_{ABC}}} = (0;0; - 18)\).
b) Mặt phẳng \((SAB)\):
- Ta cần tìm hai vectơ chỉ phương của mặt phẳng \((SAB)\):
\(\overrightarrow {SA} = A - S = (2 - 2; - 1 + 1;3 - 7) = (0;0; - 4),\)
\(\overrightarrow {SB} = B - S = (5 - 2;2 + 1;3 - 7) = (3;3; - 4).\)
- Vectơ pháp tuyến của mặt phẳng \((SAB)\) là tích có hướng của \(\overrightarrow {SA} \) và \(\overrightarrow {SB} \):
\(\overrightarrow {{n_{SAB}}} = \overrightarrow {SA} \times \overrightarrow {SB} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\0&0&{ - 4}\\3&3&{ - 4}\end{array}} \right| = (12; - 12;0).\)
Do đó, một vectơ pháp tuyến của mặt phẳng \((SAB)\) là \(\overrightarrow {{n_{SAB}}} = (12; - 12;0)\).
c) Mặt phẳng \((SBC)\):
- Tương tự, ta cần tìm hai vectơ chỉ phương của mặt phẳng \((SBC)\):
\(\overrightarrow {SB} = (3;3; - 4)\quad {\rm{v\`a }}\quad \overrightarrow {SC} = C - S = (8 - 2; - 1 + 1;3 - 7) = (6;0; - 4).\)
- Vectơ pháp tuyến của mặt phẳng \((SBC)\) là tích có hướng của \(\overrightarrow {SB} \) và \(\overrightarrow {SC} \):
\(\overrightarrow {{n_{SBC}}} = \overrightarrow {SB} \times \overrightarrow {SC} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\3&3&{ - 4}\\6&0&{ - 4}\end{array}} \right| = ( - 12; - 12; - 18).\)
Do đó, một vectơ pháp tuyến của mặt phẳng \((SBC)\) là:
\(\overrightarrow {{n_{SBC}}} = ( - 12; - 12; - 18)\)
* Chứng minh các mặt phẳng vuông góc
a) Mặt phẳng \((SAB)\) và \((ABC)\):
- Để kiểm tra \((SAB)\) vuông góc với \((ABC)\), ta tính tích vô hướng của \(\overrightarrow {{n_{SAB}}} \) và \(\overrightarrow {{n_{ABC}}} \):
\(\overrightarrow {{n_{SAB}}} \cdot \overrightarrow {{n_{ABC}}} = (12; - 12;0) \cdot (0;0; - 18) = 12 \times 0 + ( - 12) \times 0 + 0 \times ( - 18) = 0.\)
- Vì tích vô hướng bằng 0, nên \((SAB) \bot (ABC)\).
b) Mặt phẳng \((SAB)\) và \((SBC)\):
- Tương tự, ta tính tích vô hướng của \(\overrightarrow {{n_{SAB}}} \) và \(\overrightarrow {{n_{SBC}}} \):
\(\overrightarrow {{n_{SAB}}} \cdot \overrightarrow {{n_{SBC}}} = (12; - 12;0) \cdot ( - 12; - 12; - 18) = 12 \times ( - 12) + ( - 12) \times ( - 12) + 0 \times ( - 18) = - 144 + 144 + 0 = 0.\)
- Vì tích vô hướng bằng 0, nên \((SAB) \bot (SBC)\).
Trả lời câu hỏi Luyện tập 9 trang 49 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, viết phương trình mặt phẳng \((\alpha )\) đi qua \(A( - 3;2; - 1)\) và vuông góc với hai mặt phẳng \((P):2x - y + 3z - 1 = 0\), \((Q):x + 2y - 2z + 3 = 0\).
Phương pháp giải:
- Vectơ pháp tuyến của mặt phẳng \((\alpha )\) phải vuông góc với cả hai vectơ pháp tuyến của các mặt phẳng \((P)\) và \((Q)\).
- Từ đó, ta tìm vectơ pháp tuyến của \((\alpha )\) bằng tích có hướng của hai vectơ pháp tuyến của \((P)\) và \((Q)\).
- Sau khi có vectơ pháp tuyến của \((\alpha )\), sử dụng điểm \(A( - 3;2; - 1)\) để lập phương trình mặt phẳng \((\alpha )\).
Lời giải chi tiết:
- Vectơ pháp tuyến của mặt phẳng \((P)\) là:
\(\overrightarrow {{n_P}} = (2; - 1;3).\)
- Vectơ pháp tuyến của mặt phẳng \((Q)\) là:
\(\overrightarrow {{n_Q}} = (1;2; - 2).\)
- Vectơ pháp tuyến của mặt phẳng \((\alpha )\) phải vuông góc với cả hai vectơ \(\overrightarrow {{n_P}} \) và \(\overrightarrow {{n_Q}} \), do đó ta tìm tích có hướng của hai vectơ này:
\(\overrightarrow {{n_\alpha }} = \overrightarrow {{n_P}} \times \overrightarrow {{n_Q}} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\2&{ - 1}&3\\1&2&{ - 2}\end{array}} \right| = {\bf{i}}\left| {\begin{array}{*{20}{c}}{ - 1}&3\\2&{ - 2}\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}2&3\\1&{ - 2}\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}2&{ - 1}\\1&2\end{array}} \right|\)
Tính các định thức con:
\(\overrightarrow {{n_\alpha }} = {\bf{i}} \cdot (( - 1)( - 2) - (3)(2)) - {\bf{j}} \cdot ((2)( - 2) - (3)(1)) + {\bf{k}} \cdot ((2)(2) - ( - 1)(1))\)
\( = {\bf{i}} \cdot (2 - 6) - {\bf{j}} \cdot ( - 4 - 3) + {\bf{k}} \cdot (4 + 1)\)
\( = {\bf{i}} \cdot ( - 4) - {\bf{j}} \cdot ( - 7) + {\bf{k}} \cdot (5)\)
\( = ( - 4;7;5).\)
Vậy vectơ pháp tuyến của mặt phẳng \((\alpha )\) là \(\overrightarrow {{n_\alpha }} = ( - 4;7;5)\).
- Phương trình tổng quát của mặt phẳng \((\alpha )\) có dạng:
\( - 4(x + 3) + 7(y - 2) + 5(z + 1) = 0.\)
- Ta thế tọa độ điểm \(A( - 3;2; - 1)\) vào phương trình:
\( - 4(x + 3) + 7(y - 2) + 5(z + 1) = 0.\)
Mở rộng phương trình:
\( - 4x - 12 + 7y - 14 + 5z + 5 = 0\)
\( - 4x + 7y + 5z - 21 = 0.\)
Vậy phương trình của mặt phẳng \((\alpha )\) là:
\( - 4x + 7y + 5z - 21 = 0.\)
Mục 3 của SGK Toán 12 tập 2 tập trung vào việc giải các bài toán liên quan đến ứng dụng của tích phân trong tính diện tích hình phẳng. Đây là một phần quan trọng trong chương trình Toán 12, đòi hỏi học sinh phải nắm vững các khái niệm về tích phân xác định, phương pháp tính diện tích hình phẳng giới hạn bởi các đường cong và trục tọa độ.
Các bài tập trong mục 3 SGK Toán 12 tập 2 thường yêu cầu học sinh:
Để giải bài tập này, ta cần xác định giao điểm của hai đường cong y = x^2 và y = 4. Giải phương trình x^2 = 4, ta được x = -2 và x = 2. Diện tích hình phẳng giới hạn bởi hai đường cong này được tính bằng tích phân:
∫-22 (4 - x2) dx = [4x - (x3/3)]-22 = (8 - 8/3) - (-8 + 8/3) = 16 - 16/3 = 32/3
Diện tích hình phẳng giới hạn bởi y = sin(x) và trục Ox trên đoạn [0, π] được tính bằng tích phân:
∫0π sin(x) dx = [-cos(x)]0π = -cos(π) - (-cos(0)) = -(-1) + 1 = 2
Để tính diện tích hình phẳng này, ta cần tìm các nghiệm của phương trình x2 - 4x + 3 = 0. Giải phương trình, ta được x = 1 và x = 3. Diện tích hình phẳng được tính bằng tích phân:
∫13 -(x2 - 4x + 3) dx = ∫13 (-x2 + 4x - 3) dx = [-x3/3 + 2x2 - 3x]13 = (-9 + 18 - 9) - (-1/3 + 2 - 3) = 0 - (-4/3) = 4/3
Tích phân có rất nhiều ứng dụng trong thực tế, bao gồm:
Việc nắm vững kiến thức về tích phân và ứng dụng của tích phân là rất quan trọng đối với học sinh lớp 12. Hy vọng rằng bài giải chi tiết mục 3 trang 47, 48, 49 SGK Toán 12 tập 2 tại giaitoan.edu.vn sẽ giúp các em hiểu rõ hơn về các khái niệm này và tự tin làm bài tập.