Chào mừng các em học sinh đến với bài giải chi tiết bài tập 6.11 trang 105 SGK Toán 12 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến số phức và ứng dụng của chúng.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và phương pháp giải bài tập hiệu quả.
Trong một cuộc khảo sát tình trạng công việc trên 900 người đã có bằng tốt nghiệp trung học phổ thông ở một địa phương cho cả nam lẫn nữ, người ta thu được số liệu như Bảng 6.4.
Đề bài
Trong một cuộc khảo sát tình trạng công việc trên 900 người đã có bằng tốt nghiệp trung học phổ thông ở một địa phương cho cả nam lẫn nữ, người ta thu được số liệu như Bảng 6.4.
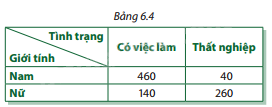
Chọn ngẫu nhiên một người trong nhóm này. Gọi A là biến cố "Người được chọn là nữ", B là biến cố "Người được chọn có việc làm".
a) Vẽ lại sơ đồ hình cây sau đây và hoàn thành kết quả ở các ô ?
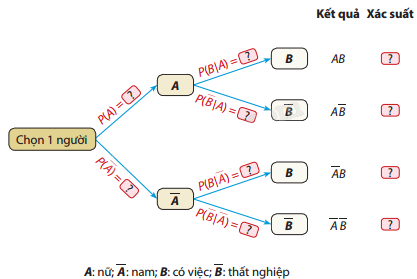
b) Tính xác suất để chọn được một người có việc làm.
c) Biết rằng đã chọn được một người có việc làm, tính xác suất để người này là nữ.
Phương pháp giải - Xem chi tiết
Xác định các xác suất và sử dụng các công thức sau:
- Xác suất có điều kiện: \(P(A|B) = \frac{{P(AB)}}{{P(B)}},\quad P(B|A) = \frac{{P(AB)}}{{P(A)}}\)
- Xác suất của phần bù: \(P(\bar A) = 1 - P(A)\)
- Xác suất toàn phần: \(P(B) = P(B|A) \cdot P(A) + P(B|\bar A) \cdot P(\bar A)\)
Lời giải chi tiết
a) Các xác suất là:
* \(P(A) = \frac{{400}}{{900}} \approx 0,444\)
* \(P(\bar A) = 1 - P(A) = 1 - 0,444 = 0,556\)
* \(P(B|A) = \frac{{140}}{{400}} = 0,35\)
* \(P(\bar B|A) = \frac{{260}}{{400}} = 0,65\)
* \(P(B|\bar A) = \frac{{460}}{{500}} = 0,92\)
* \(P(\bar B|\bar A) = \frac{{40}}{{500}} = 0,08\)
* \(P(AB) = \frac{{140}}{{900}} \approx 0,156\)
* \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\):
+ \(P(B) = P(AB) + P(\bar AB)\): \(P(B) = \frac{{140}}{{900}} + \frac{{460}}{{900}} = \frac{{600}}{{900}} = 0,667\)
+ \(P(A|B) = \frac{{\frac{{140}}{{900}}}}{{0,667}} \approx 0,21\)
* \(P(\bar AB) = \frac{{460}}{{900}} \approx 0,511\)
* \(P(\bar A\bar B) = \frac{{40}}{{900}} \approx 0,044\)
b) Xác suất để chọn được một người có việc làm: \(P(B) = 0,667{\mkern 1mu} (66,7\% ).\)
c) Xác suất để người có việc làm là nữ: \(P(A|B) \approx 0,234{\mkern 1mu} (23,4\% ).\)
Bài tập 6.11 trang 105 SGK Toán 12 tập 2 là một bài toán quan trọng trong chương trình học về số phức. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về số phức, bao gồm:
Bài tập 6.11 thường yêu cầu học sinh thực hiện các thao tác sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài tập yêu cầu tìm phần thực và phần ảo của số phức z = (2 + 3i)(1 - i).
Bước 1: Thực hiện phép nhân
z = (2 + 3i)(1 - i) = 2(1 - i) + 3i(1 - i) = 2 - 2i + 3i - 3i² = 2 + i - 3(-1) = 2 + i + 3 = 5 + i
Bước 2: Xác định phần thực và phần ảo
Từ kết quả trên, ta thấy phần thực của z là 5 và phần ảo của z là 1.
Ngoài bài tập 6.11, còn rất nhiều bài tập tương tự trong SGK Toán 12 tập 2. Để giải các bài tập này, học sinh cần:
Số phức không chỉ là một khái niệm trừu tượng trong toán học mà còn có nhiều ứng dụng quan trọng trong thực tế, đặc biệt trong các lĩnh vực:
Để học tốt về số phức, các em nên:
Bài tập 6.11 trang 105 SGK Toán 12 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về số phức. Hy vọng với lời giải chi tiết và các phương pháp giải bài tập mà chúng tôi đã cung cấp, các em sẽ tự tin hơn khi đối mặt với các bài toán tương tự.