Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 2 trang 59, 60, 61, 62, 63 SGK Toán 12 tập 2. Hãy cùng bắt đầu!
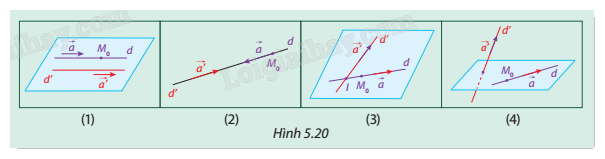
Cho hai đường thẳng d và d’ có các vectơ chỉ phương lần lượt là \(\overrightarrow a \) và \(\overrightarrow {a'} \), \({M_0} \in d\) như Hình 5.20.
Trả lời câu hỏi Luyện tập 5 trang 62 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, xét vị trí tương đối của các cặp đường thẳng sau:
a) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 3 - t}\\{y = 4 + t}\\{z = 5 - 2t}\end{array}} \right.\quad (t \in \mathbb{R})\) và \(d':\left\{ {\begin{array}{*{20}{l}}{x = 2 - 3t'}\\{y = 5 + 3t'}\\{z = 3 - 6t'}\end{array}} \right.\quad (t' \in \mathbb{R}){\rm{ }}\)
b) \(d:\frac{{x - 1}}{1} = \frac{{y - 2}}{3} = \frac{{z - 3}}{{ - 1}}\) và \(d':\frac{{x - 2}}{{ - 2}} = \frac{{y + 2}}{1} = \frac{{z - 1}}{3}\)
c) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = 2 + t}\\{z = - 3 + 3t}\end{array}} \right.\quad (t \in \mathbb{R}){\rm{ }}\) và \(d':\frac{{x - 2}}{1} = \frac{{y + 3}}{2} = \frac{{z - 1}}{3}{\rm{ }}\)
Phương pháp giải:
- Hai đường thẳng song song: Nếu chúng có vectơ chỉ phương cùng phương và không có điểm chung.
- Hai đường thẳng cắt nhau: Nếu chúng không cùng phương và có duy nhất một điểm chung.
- Hai đường thẳng chéo nhau: Nếu chúng không nằm trong cùng một mặt phẳng và không có điểm chung.
- Hai đường thẳng trùng nhau: Nếu chúng cùng phương và có vô số điểm chung.
Lời giải chi tiết:
a)
- Vectơ chỉ phương của đường thẳng \(d\): \(\overrightarrow {{u_d}} = ( - 1;1; - 2)\)
- Vectơ chỉ phương của đường thẳng\(d'\): \(\overrightarrow {{u_{d'}}} = ( - 3;3; - 6)\)
Nhận thấy: \(\overrightarrow {{u_d}} = k\overrightarrow {{u_{d'}}} \) với \(k = \frac{1}{3}\)
Vậy hai đường thẳng song song.
b)
- Vectơ chỉ phương của đường thẳng \(d\): \(\overrightarrow {{u_d}} = (1;3; - 1)\)
- Vectơ chỉ phương của đường thẳng\(d'\): \(\overrightarrow {{u_{d'}}} = ( - 2;1;3)\)
Nhận thấy không tồn tại giá trị k để \(\overrightarrow {{u_d}} = k\overrightarrow {{u_{d'}}} \) và \(\overrightarrow {{u_d}} .\overrightarrow {{u_{d'}}} = 1.( - 2) + 3.1 + ( - 1).3 = - 2 \ne 0\) nên hai đường thẳng không song song cũng không vuông góc.
Để kiểm tra xem hai đường thẳng có cắt nhau không, ta giải hệ phương trình tham số từ hai đường thẳng.
Phương trình tham số của \(d\):
\(\frac{{x - 1}}{1} = \frac{{y - 2}}{3} = \frac{{z - 3}}{{ - 1}}\quad {\rm{hay}}\quad \left\{ {\begin{array}{*{20}{l}}{x = 1 + t}\\{y = 2 + 3t}\\{z = 3 - t}\end{array}} \right.\quad \quad t \in \mathbb{R}\)
Phương trình tham số của \(d'\)
\(\frac{{x - 2}}{{ - 2}} = \frac{{y + 2}}{1} = \frac{{z - 1}}{3}\quad {\rm{hay}}\quad \left\{ {\begin{array}{*{20}{l}}{x = 2 - 2t'}\\{y = - 2 + t'}\\{z = 1 + 3t'}\end{array}} \right.\quad \quad t' \in \mathbb{R}\)
Giải hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{1 + t = 2 - 2t'}\\{2 + 3t = - 2 + t'}\\{3 - t = 1 + 3t'}\end{array}} \right.\)
Từ phương trình thứ nhất:
\(t = 1 - 2t'\)
Thay vào phương trình thứ hai:
\(2 + 3(1 - 2t') = - 2 + t'\quad \Rightarrow \quad 5 - 6t' = - 2 + t'\quad \Rightarrow \quad 7 = 7t'\quad \Rightarrow \quad t' = 1\)
Thay \(t' = 1\) vào \(t = 1 - 2t'\), ta có \(t = - 1\). Thay \(t = - 1\) và \(t' = 1\) vào phương trình thứ ba:
\(3 - ( - 1) = 1 + 3(1)\quad \Rightarrow \quad 4 = 4\)
Điều này đúng.
Hai đường thẳng \(d\) và \(d'\) cắt nhau tại điểm \((x,y,z) = (0, - 1,4)\).
c)
- Vectơ chỉ phương của \(d\) là \(\overrightarrow {{u_d}} = (2,1,3)\).
- Vectơ chỉ phương của \(d'\) là \(\overrightarrow {{u_{d'}}} = (1,2,3)\).
\(\frac{2}{1} \ne \frac{1}{2} \ne \frac{3}{3}\)
Do đó, \(d\) và \(d'\) không song song.
Giải hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{1 + 2t = 2 + t'}\\{2 + t = - 3 + 2t'}\\{ - 3 + 3t = 1 + 3t'}\end{array}} \right.\)
Từ phương trình thứ nhất: \(t' = 2t - 1\). Thay vào phương trình thứ hai: \(t = \frac{7}{3}\), \(t' = \frac{{11}}{3}\). Thay vào phương trình thứ ba: Điều này sai
Vậy hai đường thẳng \(d\) và \(d'\) chéo nhau.
Trả lời câu hỏi Luyện tập 6 trang 62 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tìm hai đường thẳng vuông góc nhau trong ba đường thẳng sau đây: \({d_1}:\frac{{x - 5}}{1} = \frac{{y + 3}}{2} = \frac{{z - 3}}{{ - 2}},\quad {d_2}:\frac{{x - 2}}{{ - 3}} = \frac{{y - 3}}{1} = \frac{{z - 1}}{6},\quad {d_3}:\left\{ {\begin{array}{*{20}{l}}{x = 1 - 2t}\\{y = 3}\\{z = 4 - t}\end{array}} \right.\)
Phương pháp giải:
- Tìm vectơ chỉ phương của các đường thẳng \({d_1},{d_2}\) và \({d_3}\).
- Kiểm tra tích vô hướng giữa các cặp vectơ chỉ phương để tìm ra hai đường thẳng vuông góc.
Lời giải chi tiết:
- Đường thẳng \({d_1}\): vectơ chỉ phương \(\overrightarrow {{u_1}} = (1,2, - 2)\).
- Đường thẳng \({d_2}\): vectơ chỉ phương \(\overrightarrow {{u_2}} = ( - 3,1,6)\).
- Đường thẳng \({d_3}\): vectơ chỉ phương \(\overrightarrow {{u_3}} = ( - 2,0, - 1)\).
- Tích vô hướng giữa \(\overrightarrow {{u_1}} = (1,2, - 2)\) và \(\overrightarrow {{u_2}} = ( - 3,1,6)\):
\(\overrightarrow {{u_1}} \cdot \overrightarrow {{u_2}} = 1 \cdot ( - 3) + 2 \cdot 1 + ( - 2) \cdot 6 = - 3 + 2 - 12 = - 13\quad ({\rm{kh\^o ng vu\^o ng g\'o c}}).\)
- Tích vô hướng giữa \(\overrightarrow {{u_1}} = (1,2, - 2)\) và \(\overrightarrow {{u_3}} = ( - 2,0, - 1)\):
\(\overrightarrow {{u_1}} \cdot \overrightarrow {{u_3}} = 1 \cdot ( - 2) + 2 \cdot 0 + ( - 2) \cdot ( - 1) = - 2 + 0 + 2 = 0\quad ({\rm{vu\^o ng g\'o c}}).\)
- Tích vô hướng giữa \(\overrightarrow {{u_2}} = ( - 3,1,6)\) và \(\overrightarrow {{u_3}} = ( - 2,0, - 1)\):
\(\overrightarrow {{u_2}} \cdot \overrightarrow {{u_3}} = ( - 3) \cdot ( - 2) + 1 \cdot 0 + 6 \cdot ( - 1) = 6 + 0 - 6 = 0\quad ({\rm{vu\^o ng g\'o c}}).\)
- Hai đường thẳng \({d_1}\) và \({d_3}\) vuông góc với nhau (do \(\overrightarrow {{u_1}} \cdot \overrightarrow {{u_3}} = 0\)).
- Hai đường thẳng \({d_2}\) và \({d_3}\) cũng vuông góc với nhau (do \(\overrightarrow {{u_2}} \cdot \overrightarrow {{u_3}} = 0\)).
Trả lời câu hỏi Hoạt động 6 trang 62 SGK Toán 12 Cùng khám phá
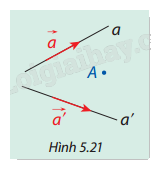
Trong không gian, cho hai đường thẳng a và a' lần lượt là giá của hai vectơ (khác \(\overrightarrow 0 \)) \(\vec a\) và \(\vec a'\) (Hình 5.21). Từ một điểm A bất kỳ, vẽ hai đường thẳng d và d' lần lượt song song với a và a'.
a) Hỏi a và a' có phải lần lượt là vectơ chỉ phương của d và d' không? Vì sao?
b) Nếu \(d \bot d'\), thì \(\vec a\) và \(\vec a'\) có vuông góc nhau không? Vì sao?
Phương pháp giải:
Hai đường thẳng vuông góc nếu và chỉ nếu tích vô hướng của hai vectơ chỉ phương tương ứng bằng 0, nghĩa là:
\(\vec a \cdot \vec a' = 0\)
Lời giải chi tiết:
a) Vectơ chỉ phương của d và d' là lần lượt \(\vec a\) và \(\vec a'\) vì các đường thẳng được kẻ song song với đường thẳng gốc a và a'.
b) Nếu \(d \bot d'\), thì \(\vec a\) và \(\vec a'\) có vuông góc nhau. Điều này đúng vì tính vuông góc của hai đường thẳng tương ứng với tính vuông góc của hai vectơ chỉ phương, nghĩa là:
\(\vec a \cdot \vec a' = 0\)
Trả lời câu hỏi vận dụng 2 trang 63 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz cho trước (1 đơn vị = 1 cm), có một chú kiến vàng và một chú kiến đen bò trên hai sợi dây thẳng khác nhau. Giả sử tại thời điểm \(t\) (tính bằng phút), kiến vàng ở vị trí \((6 + t;8 - t;3 + t)\) trên đường thẳng \({d_1}\). Cùng thời điểm đó, kiến đen ở vị trí
\((1 + t;2 + t;2t)\) trên đường thẳng \({d_2}\).
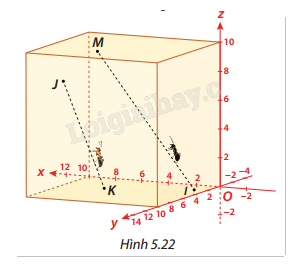
a) Chứng minh rằng hai chú kiến bò trên hai đường thẳng chéo nhau.
b) Tính khoảng cách giữa hai chú kiến tại các thời điểm \(t = 0\) và \(t = 10\).
c) Hỏi tại thời điểm nào thì khoảng cách giữa hai chú kiến là nhỏ nhất? Tính khoảng cách đó.
Phương pháp giải:
a)
- Kiểm tra xem hai đường thẳng có song song không bằng cách so sánh vectơ chỉ phương.
- Kiểm tra xem hai đường thẳng có cắt nhau không bằng cách giải hệ phương trình.
b)
Tại mỗi thời điểm t, tính tọa độ hai điểm trên hai đường thẳng tương ứng.
Sử dụng công thức khoảng cách giữa hai điểm trong không gian 3 chiều:
\(d = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}} \)
để tính khoảng cách giữa hai điểm tại các thời điểm yêu cầu.
c)
- Biểu diễn khoảng cách giữa hai điểm dưới dạng hàm theo t.
- Sử dụng phương pháp tìm cực trị của hàm số (tính đạo hàm và giải phương trình đạo hàm bằng 0) để tìm giá trị t tại đó khoảng cách là nhỏ nhất.
Lời giải chi tiết:
a)
- Vectơ chỉ phương của đường thẳng \({d_1}\) là: \(\overrightarrow {{u_1}} = (1, - 1,1)\).
- Vectơ chỉ phương của đường thẳng \({d_2}\) là: \(\overrightarrow {{u_2}} = (1,1,2)\).
Ta thấy hai vectơ chỉ phương \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không song song với nhau vì không có tỉ lệ giữa các tọa độ của hai vectơ. Vậy hai đường thẳng không song song.
Để kiểm tra xem hai đường thẳng có cắt nhau không, ta viết phương trình vị trí của hai điểm trên đường thẳng:
- Với \({d_1}\), điểm có tọa độ: \({M_1}(6 + t,8 - t,3 + t)\).
- Với \({d_2}\), điểm có tọa độ: \({M_2}(1 + t,2 + t,2t)\).
Giải hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{6 + t = 1 + t}\\{8 - t = 2 + t}\\{3 + t = 2t}\end{array}} \right.\)
Hệ phương trình này không có nghiệm. Do đó, hai đường thẳng không cắt nhau nên hai đường thẳng chéo nhau.
b)
Tại \(t = 0\), tọa độ của hai chú kiến là:
- Kiến vàng: \({M_1}(6,8,3)\).
- Kiến đen: \({M_2}(1,2,0)\).
Khoảng cách giữa hai chú kiến:
\(d = \sqrt {{{(1 - 6)}^2} + {{(2 - 8)}^2} + {{(0 - 3)}^2}} = \sqrt {25 + 36 + 9} = \sqrt {70} \approx 8.37{\mkern 1mu} {\rm{cm}}.\)
Tại \(t = 10\), tọa độ của hai chú kiến là:
- Kiến vàng: \({M_1}(16, - 2,13)\).
- Kiến đen: \({M_2}(11,12,20)\).
Khoảng cách giữa hai chú kiến:
\(d = \sqrt {{{(11 - 16)}^2} + {{(12 + 2)}^2} + {{(20 - 13)}^2}} = \sqrt {25 + 196 + 49} = \sqrt {270} \approx 16.43{\mkern 1mu} {\rm{cm}}.\)
c)
Khoảng cách giữa hai chú kiến là hàm số:
\(d(t) = \sqrt {{{(1 + t - (6 + t))}^2} + {{(2 + t - (8 - t))}^2} + {{(2t - (3 + t))}^2}} .\)
Rút gọn biểu thức:
\(d(t) = \sqrt {{{( - 5)}^2} + {{( - 6 + 2t)}^2} + {{(t - 3)}^2}} = \sqrt {25 + {{( - 6 + 2t)}^2} + {{(t - 3)}^2}} .\)
\(d(t) = \sqrt {25 + (4{t^2} - 24t + 36) + ({t^2} - 6t + 9)} = \sqrt {5{t^2} - 30t + 70} .\)
Tìm giá trị nhỏ nhất của hàm số \(d(t)\) bằng cách tính đạo hàm:
\(d'(t) = \frac{1}{{2\sqrt {5{t^2} - 30t + 70} }}(10t - 30) = 0.\)
Giải phương trình: \(10t - 30 = 0\) cho \(t = 3\). Thay \(t = 3\) vào biểu thức khoảng cách:
\(d(3) = \sqrt {5{{(3)}^2} - 30(3) + 70} = \sqrt {45 - 90 + 70} = \sqrt {25} = 5{\mkern 1mu} {\rm{cm}}.\)
Vậy khoảng cách nhỏ nhất giữa hai chú kiến là 5 cm tại thời điểm \(t = 3\).
Trả lời câu hỏi Hoạt động 5 trang 59 SGK Toán 12 Cùng khám phá
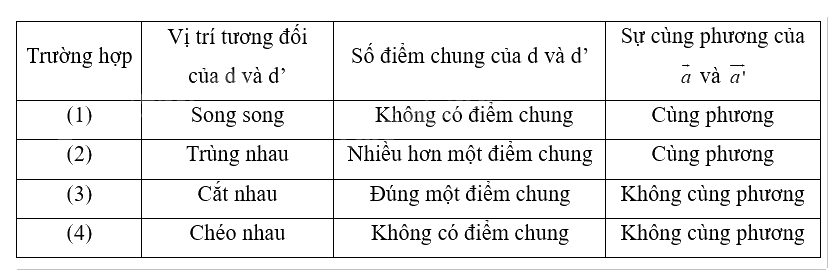
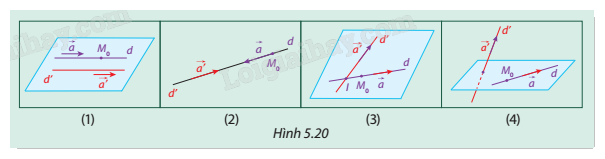
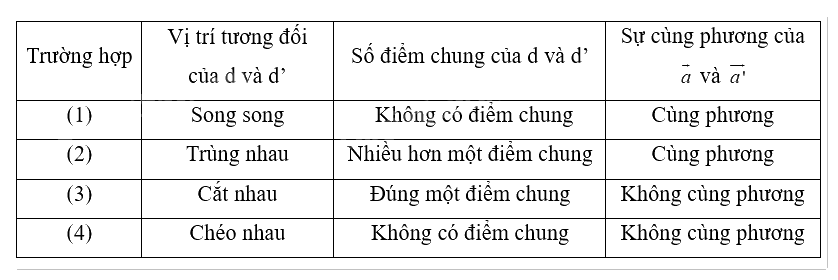
Cho hai đường thẳng d và d’ có các vectơ chỉ phương lần lượt là \(\overrightarrow a \) và \(\overrightarrow {a'} \), \({M_0} \in d\) như Hình 5.20.
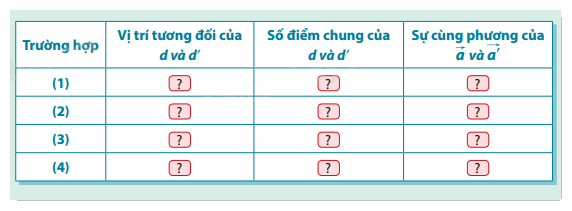
Chọn các cụm từ thích hợp (song song, cắt nhau, chéo nhau, trùng nhau, cùng phương, không cùng phương, không có điểm chung, đúng một điểm chung, nhiều hơn một điểm chung cho các ô  trong bảng sau:
trong bảng sau:
Phương pháp giải:
- Song song: Hai đường thẳng song song nếu chúng cùng phương nhưng không cắt nhau.
- Cắt nhau: Hai đường thẳng cắt nhau nếu chúng giao nhau tại một điểm và không cùng phương.
- Chéo nhau: Hai đường thẳng chéo nhau nếu chúng không cùng nằm trên một mặt phẳng và không giao nhau.
- Trùng nhau: Hai đường thẳng trùng nhau nếu chúng cùng phương và có vô số điểm chung.
- Cùng phương: Hai đường thẳng cùng phương nếu vectơ chỉ phương của chúng cùng phương hoặc song song.
Lời giải chi tiết:
Trả lời câu hỏi Hoạt động 5 trang 59 SGK Toán 12 Cùng khám phá
Cho hai đường thẳng d và d’ có các vectơ chỉ phương lần lượt là \(\overrightarrow a \) và \(\overrightarrow {a'} \), \({M_0} \in d\) như Hình 5.20.
Chọn các cụm từ thích hợp (song song, cắt nhau, chéo nhau, trùng nhau, cùng phương, không cùng phương, không có điểm chung, đúng một điểm chung, nhiều hơn một điểm chung cho các ô  trong bảng sau:
trong bảng sau:
Phương pháp giải:
- Song song: Hai đường thẳng song song nếu chúng cùng phương nhưng không cắt nhau.
- Cắt nhau: Hai đường thẳng cắt nhau nếu chúng giao nhau tại một điểm và không cùng phương.
- Chéo nhau: Hai đường thẳng chéo nhau nếu chúng không cùng nằm trên một mặt phẳng và không giao nhau.
- Trùng nhau: Hai đường thẳng trùng nhau nếu chúng cùng phương và có vô số điểm chung.
- Cùng phương: Hai đường thẳng cùng phương nếu vectơ chỉ phương của chúng cùng phương hoặc song song.
Lời giải chi tiết:
Trả lời câu hỏi Luyện tập 5 trang 62 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, xét vị trí tương đối của các cặp đường thẳng sau:
a) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 3 - t}\\{y = 4 + t}\\{z = 5 - 2t}\end{array}} \right.\quad (t \in \mathbb{R})\) và \(d':\left\{ {\begin{array}{*{20}{l}}{x = 2 - 3t'}\\{y = 5 + 3t'}\\{z = 3 - 6t'}\end{array}} \right.\quad (t' \in \mathbb{R}){\rm{ }}\)
b) \(d:\frac{{x - 1}}{1} = \frac{{y - 2}}{3} = \frac{{z - 3}}{{ - 1}}\) và \(d':\frac{{x - 2}}{{ - 2}} = \frac{{y + 2}}{1} = \frac{{z - 1}}{3}\)
c) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = 2 + t}\\{z = - 3 + 3t}\end{array}} \right.\quad (t \in \mathbb{R}){\rm{ }}\) và \(d':\frac{{x - 2}}{1} = \frac{{y + 3}}{2} = \frac{{z - 1}}{3}{\rm{ }}\)
Phương pháp giải:
- Hai đường thẳng song song: Nếu chúng có vectơ chỉ phương cùng phương và không có điểm chung.
- Hai đường thẳng cắt nhau: Nếu chúng không cùng phương và có duy nhất một điểm chung.
- Hai đường thẳng chéo nhau: Nếu chúng không nằm trong cùng một mặt phẳng và không có điểm chung.
- Hai đường thẳng trùng nhau: Nếu chúng cùng phương và có vô số điểm chung.
Lời giải chi tiết:
a)
- Vectơ chỉ phương của đường thẳng \(d\): \(\overrightarrow {{u_d}} = ( - 1;1; - 2)\)
- Vectơ chỉ phương của đường thẳng\(d'\): \(\overrightarrow {{u_{d'}}} = ( - 3;3; - 6)\)
Nhận thấy: \(\overrightarrow {{u_d}} = k\overrightarrow {{u_{d'}}} \) với \(k = \frac{1}{3}\)
Vậy hai đường thẳng song song.
b)
- Vectơ chỉ phương của đường thẳng \(d\): \(\overrightarrow {{u_d}} = (1;3; - 1)\)
- Vectơ chỉ phương của đường thẳng\(d'\): \(\overrightarrow {{u_{d'}}} = ( - 2;1;3)\)
Nhận thấy không tồn tại giá trị k để \(\overrightarrow {{u_d}} = k\overrightarrow {{u_{d'}}} \) và \(\overrightarrow {{u_d}} .\overrightarrow {{u_{d'}}} = 1.( - 2) + 3.1 + ( - 1).3 = - 2 \ne 0\) nên hai đường thẳng không song song cũng không vuông góc.
Để kiểm tra xem hai đường thẳng có cắt nhau không, ta giải hệ phương trình tham số từ hai đường thẳng.
Phương trình tham số của \(d\):
\(\frac{{x - 1}}{1} = \frac{{y - 2}}{3} = \frac{{z - 3}}{{ - 1}}\quad {\rm{hay}}\quad \left\{ {\begin{array}{*{20}{l}}{x = 1 + t}\\{y = 2 + 3t}\\{z = 3 - t}\end{array}} \right.\quad \quad t \in \mathbb{R}\)
Phương trình tham số của \(d'\)
\(\frac{{x - 2}}{{ - 2}} = \frac{{y + 2}}{1} = \frac{{z - 1}}{3}\quad {\rm{hay}}\quad \left\{ {\begin{array}{*{20}{l}}{x = 2 - 2t'}\\{y = - 2 + t'}\\{z = 1 + 3t'}\end{array}} \right.\quad \quad t' \in \mathbb{R}\)
Giải hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{1 + t = 2 - 2t'}\\{2 + 3t = - 2 + t'}\\{3 - t = 1 + 3t'}\end{array}} \right.\)
Từ phương trình thứ nhất:
\(t = 1 - 2t'\)
Thay vào phương trình thứ hai:
\(2 + 3(1 - 2t') = - 2 + t'\quad \Rightarrow \quad 5 - 6t' = - 2 + t'\quad \Rightarrow \quad 7 = 7t'\quad \Rightarrow \quad t' = 1\)
Thay \(t' = 1\) vào \(t = 1 - 2t'\), ta có \(t = - 1\). Thay \(t = - 1\) và \(t' = 1\) vào phương trình thứ ba:
\(3 - ( - 1) = 1 + 3(1)\quad \Rightarrow \quad 4 = 4\)
Điều này đúng.
Hai đường thẳng \(d\) và \(d'\) cắt nhau tại điểm \((x,y,z) = (0, - 1,4)\).
c)
- Vectơ chỉ phương của \(d\) là \(\overrightarrow {{u_d}} = (2,1,3)\).
- Vectơ chỉ phương của \(d'\) là \(\overrightarrow {{u_{d'}}} = (1,2,3)\).
\(\frac{2}{1} \ne \frac{1}{2} \ne \frac{3}{3}\)
Do đó, \(d\) và \(d'\) không song song.
Giải hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{1 + 2t = 2 + t'}\\{2 + t = - 3 + 2t'}\\{ - 3 + 3t = 1 + 3t'}\end{array}} \right.\)
Từ phương trình thứ nhất: \(t' = 2t - 1\). Thay vào phương trình thứ hai: \(t = \frac{7}{3}\), \(t' = \frac{{11}}{3}\). Thay vào phương trình thứ ba: Điều này sai
Vậy hai đường thẳng \(d\) và \(d'\) chéo nhau.
Trả lời câu hỏi Hoạt động 6 trang 62 SGK Toán 12 Cùng khám phá
Trong không gian, cho hai đường thẳng a và a' lần lượt là giá của hai vectơ (khác \(\overrightarrow 0 \)) \(\vec a\) và \(\vec a'\) (Hình 5.21). Từ một điểm A bất kỳ, vẽ hai đường thẳng d và d' lần lượt song song với a và a'.
a) Hỏi a và a' có phải lần lượt là vectơ chỉ phương của d và d' không? Vì sao?
b) Nếu \(d \bot d'\), thì \(\vec a\) và \(\vec a'\) có vuông góc nhau không? Vì sao?
Phương pháp giải:
Hai đường thẳng vuông góc nếu và chỉ nếu tích vô hướng của hai vectơ chỉ phương tương ứng bằng 0, nghĩa là:
\(\vec a \cdot \vec a' = 0\)
Lời giải chi tiết:
a) Vectơ chỉ phương của d và d' là lần lượt \(\vec a\) và \(\vec a'\) vì các đường thẳng được kẻ song song với đường thẳng gốc a và a'.
b) Nếu \(d \bot d'\), thì \(\vec a\) và \(\vec a'\) có vuông góc nhau. Điều này đúng vì tính vuông góc của hai đường thẳng tương ứng với tính vuông góc của hai vectơ chỉ phương, nghĩa là:
\(\vec a \cdot \vec a' = 0\)
Trả lời câu hỏi Luyện tập 6 trang 62 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tìm hai đường thẳng vuông góc nhau trong ba đường thẳng sau đây: \({d_1}:\frac{{x - 5}}{1} = \frac{{y + 3}}{2} = \frac{{z - 3}}{{ - 2}},\quad {d_2}:\frac{{x - 2}}{{ - 3}} = \frac{{y - 3}}{1} = \frac{{z - 1}}{6},\quad {d_3}:\left\{ {\begin{array}{*{20}{l}}{x = 1 - 2t}\\{y = 3}\\{z = 4 - t}\end{array}} \right.\)
Phương pháp giải:
- Tìm vectơ chỉ phương của các đường thẳng \({d_1},{d_2}\) và \({d_3}\).
- Kiểm tra tích vô hướng giữa các cặp vectơ chỉ phương để tìm ra hai đường thẳng vuông góc.
Lời giải chi tiết:
- Đường thẳng \({d_1}\): vectơ chỉ phương \(\overrightarrow {{u_1}} = (1,2, - 2)\).
- Đường thẳng \({d_2}\): vectơ chỉ phương \(\overrightarrow {{u_2}} = ( - 3,1,6)\).
- Đường thẳng \({d_3}\): vectơ chỉ phương \(\overrightarrow {{u_3}} = ( - 2,0, - 1)\).
- Tích vô hướng giữa \(\overrightarrow {{u_1}} = (1,2, - 2)\) và \(\overrightarrow {{u_2}} = ( - 3,1,6)\):
\(\overrightarrow {{u_1}} \cdot \overrightarrow {{u_2}} = 1 \cdot ( - 3) + 2 \cdot 1 + ( - 2) \cdot 6 = - 3 + 2 - 12 = - 13\quad ({\rm{kh\^o ng vu\^o ng g\'o c}}).\)
- Tích vô hướng giữa \(\overrightarrow {{u_1}} = (1,2, - 2)\) và \(\overrightarrow {{u_3}} = ( - 2,0, - 1)\):
\(\overrightarrow {{u_1}} \cdot \overrightarrow {{u_3}} = 1 \cdot ( - 2) + 2 \cdot 0 + ( - 2) \cdot ( - 1) = - 2 + 0 + 2 = 0\quad ({\rm{vu\^o ng g\'o c}}).\)
- Tích vô hướng giữa \(\overrightarrow {{u_2}} = ( - 3,1,6)\) và \(\overrightarrow {{u_3}} = ( - 2,0, - 1)\):
\(\overrightarrow {{u_2}} \cdot \overrightarrow {{u_3}} = ( - 3) \cdot ( - 2) + 1 \cdot 0 + 6 \cdot ( - 1) = 6 + 0 - 6 = 0\quad ({\rm{vu\^o ng g\'o c}}).\)
- Hai đường thẳng \({d_1}\) và \({d_3}\) vuông góc với nhau (do \(\overrightarrow {{u_1}} \cdot \overrightarrow {{u_3}} = 0\)).
- Hai đường thẳng \({d_2}\) và \({d_3}\) cũng vuông góc với nhau (do \(\overrightarrow {{u_2}} \cdot \overrightarrow {{u_3}} = 0\)).
Trả lời câu hỏi vận dụng 2 trang 63 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz cho trước (1 đơn vị = 1 cm), có một chú kiến vàng và một chú kiến đen bò trên hai sợi dây thẳng khác nhau. Giả sử tại thời điểm \(t\) (tính bằng phút), kiến vàng ở vị trí \((6 + t;8 - t;3 + t)\) trên đường thẳng \({d_1}\). Cùng thời điểm đó, kiến đen ở vị trí
\((1 + t;2 + t;2t)\) trên đường thẳng \({d_2}\).
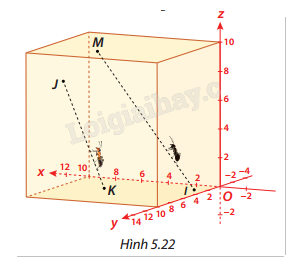
a) Chứng minh rằng hai chú kiến bò trên hai đường thẳng chéo nhau.
b) Tính khoảng cách giữa hai chú kiến tại các thời điểm \(t = 0\) và \(t = 10\).
c) Hỏi tại thời điểm nào thì khoảng cách giữa hai chú kiến là nhỏ nhất? Tính khoảng cách đó.
Phương pháp giải:
a)
- Kiểm tra xem hai đường thẳng có song song không bằng cách so sánh vectơ chỉ phương.
- Kiểm tra xem hai đường thẳng có cắt nhau không bằng cách giải hệ phương trình.
b)
Tại mỗi thời điểm t, tính tọa độ hai điểm trên hai đường thẳng tương ứng.
Sử dụng công thức khoảng cách giữa hai điểm trong không gian 3 chiều:
\(d = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}} \)
để tính khoảng cách giữa hai điểm tại các thời điểm yêu cầu.
c)
- Biểu diễn khoảng cách giữa hai điểm dưới dạng hàm theo t.
- Sử dụng phương pháp tìm cực trị của hàm số (tính đạo hàm và giải phương trình đạo hàm bằng 0) để tìm giá trị t tại đó khoảng cách là nhỏ nhất.
Lời giải chi tiết:
a)
- Vectơ chỉ phương của đường thẳng \({d_1}\) là: \(\overrightarrow {{u_1}} = (1, - 1,1)\).
- Vectơ chỉ phương của đường thẳng \({d_2}\) là: \(\overrightarrow {{u_2}} = (1,1,2)\).
Ta thấy hai vectơ chỉ phương \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không song song với nhau vì không có tỉ lệ giữa các tọa độ của hai vectơ. Vậy hai đường thẳng không song song.
Để kiểm tra xem hai đường thẳng có cắt nhau không, ta viết phương trình vị trí của hai điểm trên đường thẳng:
- Với \({d_1}\), điểm có tọa độ: \({M_1}(6 + t,8 - t,3 + t)\).
- Với \({d_2}\), điểm có tọa độ: \({M_2}(1 + t,2 + t,2t)\).
Giải hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{6 + t = 1 + t}\\{8 - t = 2 + t}\\{3 + t = 2t}\end{array}} \right.\)
Hệ phương trình này không có nghiệm. Do đó, hai đường thẳng không cắt nhau nên hai đường thẳng chéo nhau.
b)
Tại \(t = 0\), tọa độ của hai chú kiến là:
- Kiến vàng: \({M_1}(6,8,3)\).
- Kiến đen: \({M_2}(1,2,0)\).
Khoảng cách giữa hai chú kiến:
\(d = \sqrt {{{(1 - 6)}^2} + {{(2 - 8)}^2} + {{(0 - 3)}^2}} = \sqrt {25 + 36 + 9} = \sqrt {70} \approx 8.37{\mkern 1mu} {\rm{cm}}.\)
Tại \(t = 10\), tọa độ của hai chú kiến là:
- Kiến vàng: \({M_1}(16, - 2,13)\).
- Kiến đen: \({M_2}(11,12,20)\).
Khoảng cách giữa hai chú kiến:
\(d = \sqrt {{{(11 - 16)}^2} + {{(12 + 2)}^2} + {{(20 - 13)}^2}} = \sqrt {25 + 196 + 49} = \sqrt {270} \approx 16.43{\mkern 1mu} {\rm{cm}}.\)
c)
Khoảng cách giữa hai chú kiến là hàm số:
\(d(t) = \sqrt {{{(1 + t - (6 + t))}^2} + {{(2 + t - (8 - t))}^2} + {{(2t - (3 + t))}^2}} .\)
Rút gọn biểu thức:
\(d(t) = \sqrt {{{( - 5)}^2} + {{( - 6 + 2t)}^2} + {{(t - 3)}^2}} = \sqrt {25 + {{( - 6 + 2t)}^2} + {{(t - 3)}^2}} .\)
\(d(t) = \sqrt {25 + (4{t^2} - 24t + 36) + ({t^2} - 6t + 9)} = \sqrt {5{t^2} - 30t + 70} .\)
Tìm giá trị nhỏ nhất của hàm số \(d(t)\) bằng cách tính đạo hàm:
\(d'(t) = \frac{1}{{2\sqrt {5{t^2} - 30t + 70} }}(10t - 30) = 0.\)
Giải phương trình: \(10t - 30 = 0\) cho \(t = 3\). Thay \(t = 3\) vào biểu thức khoảng cách:
\(d(3) = \sqrt {5{{(3)}^2} - 30(3) + 70} = \sqrt {45 - 90 + 70} = \sqrt {25} = 5{\mkern 1mu} {\rm{cm}}.\)
Vậy khoảng cách nhỏ nhất giữa hai chú kiến là 5 cm tại thời điểm \(t = 3\).
Mục 2 của SGK Toán 12 tập 2 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Giaitoan.edu.vn sẽ cung cấp hướng dẫn chi tiết từng bước, giúp các em hiểu rõ bản chất của vấn đề và áp dụng vào các bài tập tương tự.
Trang 59 thường chứa các bài tập vận dụng kiến thức cơ bản của mục 2. Chúng ta sẽ bắt đầu với bài tập 1, sau đó đến bài tập 2 và các bài tập tiếp theo. Mỗi bài tập sẽ được giải thích rõ ràng, kèm theo các bước thực hiện cụ thể.
Trang 60 có thể chứa các bài tập nâng cao hơn, đòi hỏi học sinh phải vận dụng linh hoạt kiến thức và kỹ năng đã học. Chúng ta sẽ tiếp tục giải quyết từng bài tập một cách cẩn thận và chi tiết.
Các bài tập trên trang 61 thường liên quan đến việc ứng dụng kiến thức vào các bài toán thực tế. Chúng ta sẽ phân tích đề bài, xác định các yếu tố quan trọng và đưa ra lời giải phù hợp.
Trang 62 có thể chứa các bài tập tổng hợp, yêu cầu học sinh phải kết hợp nhiều kiến thức khác nhau để giải quyết. Chúng ta sẽ chia nhỏ bài toán thành các phần nhỏ hơn, giải quyết từng phần và kết hợp lại để có được kết quả cuối cùng.
Trang 63 thường là phần bài tập ôn tập, giúp học sinh củng cố kiến thức đã học trong mục 2. Chúng ta sẽ giải quyết các bài tập này một cách nhanh chóng và chính xác.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục kiến thức Toán học. Chúng tôi hy vọng rằng với những lời giải chi tiết và dễ hiểu này, các em sẽ học tập hiệu quả hơn và đạt được kết quả tốt nhất.
| Công thức | Mô tả |
|---|---|
| Công thức 1 | Giải thích công thức 1 |
| Công thức 2 | Giải thích công thức 2 |