Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 4.42 trang 39 SGK Toán 12 tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến cho bạn những tài liệu học tập chất lượng cao, giúp bạn nắm vững kiến thức và đạt kết quả tốt nhất trong môn Toán.
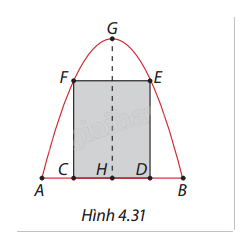
Một cái cổng hình parabol như Hình 4.31. Chiều cao \(GH = 4{\mkern 1mu} {\rm{m}}\), chiều rộng \(AB = 4{\mkern 1mu} {\rm{m}},AC = BD = 0,9{\mkern 1mu} {\rm{m}}\). Người ta làm hai cánh cổng khi đóng lại là hình chữ nhật \(CDEF\) tô đậm với giá 1.200.000 đồng/m², phần còn lại làm khung hoa sắt với giá 900.000 đồng/m².
Đề bài
Một cái cổng hình parabol như Hình 4.31. Chiều cao \(GH = 4{\mkern 1mu} {\rm{m}}\), chiều rộng \(AB = 4{\mkern 1mu} {\rm{m}},AC = BD = 0,9{\mkern 1mu} {\rm{m}}\). Người ta làm hai cánh cổng khi đóng lại là hình chữ nhật \(CDEF\) tô đậm với giá 1.200.000 đồng/m², phần còn lại làm khung hoa sắt với giá 900.000 đồng/m².
A. 11 445 000 đồng.
B. 4 077 000 đồng.
C. 7 368 000 đồng.
D. 11 370 000 đồng.
Phương pháp giải - Xem chi tiết
- Tính diện tích phần hình chữ nhật và diện tích phần khung parabol phía trên.
- Tính tổng chi phí làm cổng dựa trên diện tích mỗi phần và giá thành từng loại vật liệu.
Lời giải chi tiết
Phương trình của parabol có dạng:
\(y = a{x^2} + bx + c\)
Từ điểm \(G(0;4)\), ta suy ra được \(c = 4\).
\(y = a{x^2} + bx + 4\)
Theo đề bài ta có \(AB = 4m\), mà \(A,\,\,B\) là hai điểm đối xứng với nhau qua trục tung và nằm trên trục hoành nên suy ra:
\(\begin{array}{l}a{.2^2} + b.2 + 4 = 0\\a.{\left( { - 2} \right)^2} + b.\left( { - 2} \right) + 4 = 0\end{array}\)
Vậy ta có phương trình parabol là:
\(y = - {x^2} + 4\)
Từ đề bài, ta suy ra được \(CH = DH = 1,1m\) nên độ dài của \(CF\) và \(DE\) là:
\(CF = DE = - {(1,1)^2} + 4 = 2,79\)
Diện tích của hình chữ nhật \(CDEF\)là:
\({S_{CDEF}} = CD \times EF = 2,2 \times 2,79 = 6,138{\mkern 1mu} {{\rm{m}}^2}\)
Diện tích phần parabol là:
\({S_{{\rm{parabol}}}} = 2.\int_0^2 {( - {x^2} + 4)} {\mkern 1mu} dx = 2.\left[ { - \frac{{{x^3}}}{3} + 4x} \right]_0^2 = 2.\left( { - \frac{8}{3} + 8} \right) = \frac{{32}}{3}\)
Diện tích phần khung sắt phía trên là:
\({S_{{\rm{khung}}}} = {S_{{\rm{parabol}}}} - {S_{CDEF}} = \frac{{32}}{3} - 6,138 \approx 4,529{{\rm{m}}^2}\)
Tính tổng chi phí:
- Chi phí làm phần hình chữ nhật là:
\(6,138 \times 1\,\,200\,\,000 = 7\,\,365\,\,600\)(đồng)
- Chi phí làm phần khung sắt là:
\(4,529 \times 900.000 = 4\,\,075\,\,800\) (đồng)
Tổng chi phí làm cổng là:
\({\rm{tongcp}} = 7\,\,365\,\,600 + 4\,\,075\,\,800 = 11\,\,441\,\,400\) (đồng)
Chọn A.
Bài tập 4.42 trang 39 SGK Toán 12 tập 2 thuộc chương trình học về Đạo hàm. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm của hàm số, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài tập 4.42 thường yêu cầu học sinh tìm đạo hàm của một hàm số, xét dấu đạo hàm để xác định khoảng đơn điệu của hàm số, hoặc tìm cực trị của hàm số.
Để minh họa, giả sử bài tập 4.42 yêu cầu tìm đạo hàm của hàm số f(x) = x3 - 3x2 + 2.
Sử dụng quy tắc đạo hàm của tổng và tích, ta có:
f'(x) = 3x2 - 6x
Để xét dấu đạo hàm, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2.
Ta lập bảng xét dấu f'(x):
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + |
Từ bảng xét dấu, ta thấy:
Hàm số f(x) = x3 - 3x2 + 2 đồng biến trên các khoảng (-∞, 0) và (2, +∞), nghịch biến trên khoảng (0, 2). Hàm số đạt cực đại tại x = 0 với giá trị là f(0) = 2 và đạt cực tiểu tại x = 2 với giá trị là f(2) = -2.
Ngoài bài tập 4.42, SGK Toán 12 tập 2 còn rất nhiều bài tập tương tự về đạo hàm. Để giải tốt các bài tập này, học sinh cần:
Đạo hàm không chỉ là một công cụ quan trọng trong toán học mà còn có nhiều ứng dụng trong thực tế, như:
Để học tốt về đạo hàm, bạn nên:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài tập 4.42 trang 39 SGK Toán 12 tập 2 và các kiến thức liên quan đến đạo hàm. Chúc bạn học tập tốt!