Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau khám phá và giải chi tiết các bài tập trong mục 2 trang 17 và 18 của sách giáo khoa Toán 12 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải và tự tin làm bài tập.
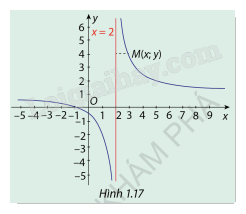
Cho hàm số \(y = \frac{{x + 1}}{{x - 2}}\)có đồ thị (C ) như Hình 1.17. a) Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)đến đường thảng x=2 khi \(x \to 2\) b) Tính các giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\)
Trả lời câu hỏi Hoạt động 2 trang 17 SGK Toán 12 Cùng khám phá
Cho hàm số \(y = \frac{{x + 1}}{{x - 2}}\)có đồ thị (C ) như Hình 1.17.
a) Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)đến đường thảng x=2 khi \(x \to 2\)
b) Tính các giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\)
Phương pháp giải:
a) Nhìn đồ thị hàm số rồi nhận xét
b) Phân tích, rồi tính \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\)
Lời giải chi tiết:
a) Dựa vào đồ thị hàm số ta thấy:
Khi và thì khoảng cách giữa đồ thị (C) với đường thẳng x = 2 càng nhỏ
b) Ta có \(f\left( x \right)\; = \frac{{x + 1}}{{x - 2}} = 1 + \frac{3}{{x - 2}} = + \infty \;\;\)
\(f\left( x \right)\; = \frac{{x + 1}}{{x - 2}} = 1 + \frac{3}{{x - 2}} = - \infty \;\;\)
Trả lời câu hỏi Luyện tập 2 trang 18 SGK Toán 12 Cùng khám phá
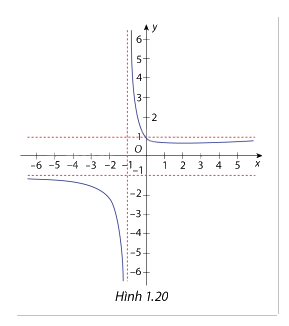
Cho hàm số \(y = f(x) = \frac{{\sqrt {{x^2} + 1} }}{{x + 1}}\) có đồ thị là đường cong như hình 1.20. Hãy xác nhận các đường tiệm cận đứng và đường tiệm cận ngang của hàm số đã cho.
Phương pháp giải:
Xét \(f(x).\)
Lời giải chi tiết:
Ta có \(\mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right)\;\)=\(\mathop {\lim }\limits_{x \to - {1^ - }} \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = - \infty \;\), \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)\;\)=\(\mathop {\lim }\limits_{x \to - {1^ + }} \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = + \infty \;\)
Suy ra x = - 1 là đường tiệm cận đứng của hàm số.
Ta có \(\mathop {\lim }\limits_{x \to + \infty } f(x)\; = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} }}{{1 + \frac{1}{x}}} = 1\;\;\), \(\mathop {\lim }\limits_{x \to - \infty } f(x)\; = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} }}{{1 + \frac{1}{x}}} = 1\;\;\)
Suy ra y = 1 là đường tiệm cận ngang của hàm số.
Trả lời câu hỏi Hoạt động 2 trang 17 SGK Toán 12 Cùng khám phá
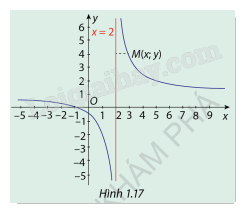
Cho hàm số \(y = \frac{{x + 1}}{{x - 2}}\)có đồ thị (C ) như Hình 1.17.
a) Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)đến đường thảng x=2 khi \(x \to 2\)
b) Tính các giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\)
Phương pháp giải:
a) Nhìn đồ thị hàm số rồi nhận xét
b) Phân tích, rồi tính \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\)
Lời giải chi tiết:
a) Dựa vào đồ thị hàm số ta thấy:
Khi và thì khoảng cách giữa đồ thị (C) với đường thẳng x = 2 càng nhỏ
b) Ta có \(f\left( x \right)\; = \frac{{x + 1}}{{x - 2}} = 1 + \frac{3}{{x - 2}} = + \infty \;\;\)
\(f\left( x \right)\; = \frac{{x + 1}}{{x - 2}} = 1 + \frac{3}{{x - 2}} = - \infty \;\;\)
Trả lời câu hỏi Luyện tập 2 trang 18 SGK Toán 12 Cùng khám phá
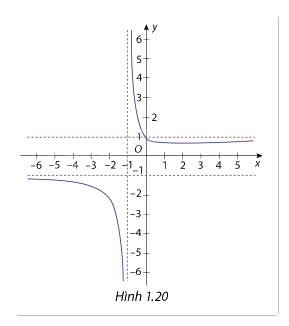
Cho hàm số \(y = f(x) = \frac{{\sqrt {{x^2} + 1} }}{{x + 1}}\) có đồ thị là đường cong như hình 1.20. Hãy xác nhận các đường tiệm cận đứng và đường tiệm cận ngang của hàm số đã cho.
Phương pháp giải:
Xét \(f(x).\)
Lời giải chi tiết:
Ta có \(\mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right)\;\)=\(\mathop {\lim }\limits_{x \to - {1^ - }} \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = - \infty \;\), \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)\;\)=\(\mathop {\lim }\limits_{x \to - {1^ + }} \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = + \infty \;\)
Suy ra x = - 1 là đường tiệm cận đứng của hàm số.
Ta có \(\mathop {\lim }\limits_{x \to + \infty } f(x)\; = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} }}{{1 + \frac{1}{x}}} = 1\;\;\), \(\mathop {\lim }\limits_{x \to - \infty } f(x)\; = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} }}{{1 + \frac{1}{x}}} = 1\;\;\)
Suy ra y = 1 là đường tiệm cận ngang của hàm số.
Mục 2 của SGK Toán 12 tập 1 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết cơ bản, các định nghĩa, định lý và công thức liên quan. Việc hiểu rõ bản chất của vấn đề cũng rất quan trọng để lựa chọn phương pháp giải phù hợp.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về... (giả sử bài tập liên quan đến giới hạn). Để giải bài tập này, ta cần:
Ví dụ: (giải chi tiết bài tập với các bước cụ thể)
Bài tập này có thể liên quan đến... (giả sử bài tập liên quan đến đạo hàm). Lời giải:
Ví dụ: (giải chi tiết bài tập với các bước cụ thể)
Bài tập này thường là một bài toán ứng dụng thực tế, yêu cầu học sinh...
Ví dụ: (giải chi tiết bài tập với các bước cụ thể)
Để giải các bài tập Toán 12 một cách hiệu quả, học sinh nên:
Khi giải bài tập Toán 12, cần chú ý:
Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải hiệu quả trên đây, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 2 trang 17, 18 SGK Toán 12 tập 1. Chúc các em học tập tốt và đạt kết quả cao!
| Công thức | Mô tả |
|---|---|
| lim (f(x) + g(x)) = lim f(x) + lim g(x) | Giới hạn của tổng |
| f'(x) = lim (f(x+h) - f(x))/h | Định nghĩa đạo hàm |