Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục 1 của Toán 12 tập 2 thường chứa các nội dung quan trọng, là nền tảng cho các kiến thức nâng cao. Việc giải đúng và hiểu sâu các bài tập trong mục này là vô cùng cần thiết.
Cho hình hộp ABCD.A'B'C'D' (Hình 5.17). Tìm bốn vectơ khác \(\overrightarrow 0 \) có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp và có giá song song hoặc trùng với đường thẳng AB.
Trả lời câu hỏi Luyện tập 2 trang 56 SGK Toán 12 Cùng khám phá
Trong không gian \(Oxyz\), cho đường thẳng \(d\) đi qua \(A(6; - 2;3)\) và có vectơ chỉ phương \(\vec a = (2;2; - 1)\).
a) Viết phương trình tham số của \(d\).
b) Tìm điểm \(M\) thuộc \(d\) biết \(OM = 7\).
Phương pháp giải:
a) Đường thẳng \(d\) đi qua điểm \(A(6; - 2;3)\) và có vectơ chỉ phương \(\vec a = (2;2; - 1)\). Phương trình tham số của đường thẳng \(d\) có dạng:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\)
Với \({M_0} = A(6; - 2;3)\) và \(\vec a = (2;2; - 1)\), thay vào ta được phương trình tham số của \(d\).
b) Tọa độ của \(M\) được biểu diễn theo tham số \(t\) từ phương trình tham số của \(d\). Dùng điều kiện \(OM = 7\), tức là khoảng cách từ gốc tọa độ \(O(0;0;0)\) đến \(M\), ta có:
\(OM = \sqrt {{x^2} + {y^2} + {z^2}} = 7\)
Thay các tọa độ của \(M(x(t),y(t),z(t))\) từ phương trình tham số vào, rồi giải phương trình để tìm \(t\), từ đó suy ra tọa độ của \(M\).
Lời giải chi tiết:
a)
Đường thẳng \(d\) đi qua điểm \(A(6; - 2;3)\) và có vectơ chỉ phương \(\vec a = (2;2; - 1)\). Phương trình tham số của đường thẳng \(d\) có dạng:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Với \(A(6; - 2;3)\) và \(\vec a = (2;2; - 1)\), phương trình tham số của đường thẳng \(d\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 6 + 2t}\\{y = - 2 + 2t}\\{z = 3 - t}\end{array}} \right.\quad (t \in \mathbb{R})\)
b)
Điểm \(M\) có tọa độ \((x,y,z)\) thuộc đường thẳng \(d\), nên tọa độ của \(M\) được biểu diễn theo tham số \(t\) như sau:
\(M(6 + 2t, - 2 + 2t,3 - t)\)
Điều kiện \(OM = 7\) nghĩa là khoảng cách từ gốc tọa độ \(O(0;0;0)\) đến \(M\) bằng 7:
\(OM = \sqrt {{x^2} + {y^2} + {z^2}} = 7\)
Thay tọa độ của \(M\) vào phương trình khoảng cách:
\(OM = \sqrt {{{(6 + 2t)}^2} + {{( - 2 + 2t)}^2} + {{(3 - t)}^2}} = 7\)
Bình phương hai vế:
\({(6 + 2t)^2} + {( - 2 + 2t)^2} + {(3 - t)^2} = 49\)
\({(6 + 2t)^2} = 36 + 24t + 4{t^2}\)
\({( - 2 + 2t)^2} = 4 - 8t + 4{t^2}\)
\({(3 - t)^2} = 9 - 6t + {t^2}\)
\((36 + 24t + 4{t^2}) + (4 - 8t + 4{t^2}) + (9 - 6t + {t^2}) = 49\)
\(49 + 10t + 9{t^2} = 49\)
\(10t + 9{t^2} = 0\)
\(t(9t + 10) = 0\)
Do đó, ta có hai nghiệm: \(t = 0\) và \(t = - \frac{{10}}{9}\)
Với \(t = 0\), tọa độ của \(M\) là:
\(M(6 + 2 \cdot 0, - 2 + 2 \cdot 0,3 - 0) = M(6, - 2,3)\)
Với \(t = - \frac{{10}}{9}\), tọa độ của \(M\) là:
\(M\left( {6 + 2 \cdot \left( { - \frac{{10}}{9}} \right), - 2 + 2 \cdot \left( { - \frac{{10}}{9}} \right),3 - \left( { - \frac{{10}}{9}} \right)} \right)\)
\(M\left( {6 - \frac{{20}}{9}, - 2 - \frac{{20}}{9},3 + \frac{{10}}{9}} \right) = M\left( {\frac{{54}}{9} - \frac{{20}}{9},\frac{{ - 18}}{9} - \frac{{20}}{9},\frac{{27}}{9} + \frac{{10}}{9}} \right)\)
\(M\left( {\frac{{34}}{9},\frac{{ - 38}}{9},\frac{{37}}{9}} \right)\)
Trả lời câu hỏi Hoạt động 3 trang 56 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho đường thẳng \(d\) qua \({M_0}({x_0};{y_0};{z_0})\) có vectơ chỉ phương \(\vec a = ({a_1};{a_2};{a_3})\). Phương trình tham số của đường thẳng là:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Giả sử \({a_1},{a_2},{a_3}\) đều khác 0. Hãy tính các tỉ số \(\frac{{x - {x_0}}}{{{a_1}}},\frac{{y - {y_0}}}{{{a_2}}},\frac{{z - {z_0}}}{{{a_3}}}\) theo \(t\) và so sánh các tỉ số này.
Phương pháp giải:
Tính các tỉ số \(\frac{{x - {x_0}}}{{{a_1}}},\frac{{y - {y_0}}}{{{a_2}}},\frac{{z - {z_0}}}{{{a_3}}}\) theo \(t\) và so sánh các tỉ số này.
Lời giải chi tiết:
Từ phương trình tham số:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\)
Ta có:
\(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}} = t\)
Các tỉ số này đều bằng \(t\), điều này chứng tỏ tất cả các tỉ số này bằng nhau, và đường thẳng \(d\) có thể viết dưới dạng phương trình chính tắc:
\(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}}\)
Trả lời câu hỏi Luyện tập 3 trang 58 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho đường thẳng \(d\) đi qua điểm \(N( - 2;3;1)\), có vectơ chỉ phương \(\vec a = (3; - 4;5)\).
a) Viết phương trình chính tắc của đường thẳng \(d\).
b) Tìm điểm \(A\) thuộc \(d\) biết \(A\) có hoành độ bằng 4.
Phương pháp giải:
a) Viết phương trình chính tắc của đường thẳng: Dựa vào phương trình tham số của đường thẳng và các tỉ số giữa tọa độ của điểm trên đường thẳng với tọa độ của điểm qua và các thành phần của vectơ chỉ phương.
b) Tìm điểm thuộc đường thẳng: Sử dụng điều kiện hoành độ của A để tìm tham số \(t\) trong phương trình tham số của đường thẳng. Từ đó tính ra tọa độ của điểm cần tìm.
Lời giải chi tiết:
a) Viết phương trình chính tắc của đường thẳng \(d\):
Phương trình tham số của đường thẳng \(d\) có dạng:
\(\left\{ {\begin{array}{*{20}{l}}{x = - 2 + 3t}\\{y = 3 - 4t}\\{z = 1 + 5t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Phương trình chính tắc của đường thẳng \(d\) là:
\(\frac{{x + 2}}{3} = \frac{{y - 3}}{{ - 4}} = \frac{{z - 1}}{5}\)
b) Tìm điểm \(A\) thuộc \(d\) biết hoành độ của A là 4:
Điểm \(A\) thuộc \(d\) có tọa độ \(A(4;y;z)\).
Suy ra: \(t = \frac{{4 + 2}}{3} = 2\)
\(y = 3 - 4.2 = - 5\) và \(z = 1 + 5.2 = 11\)
Vậy điểm A có toạ độ là \(A(4; - 5;11)\)
Trả lời câu hỏi Hoạt động 4 trang 58 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho đường thẳng \(d\) qua hai điểm phân biệt \(A({x_A};{y_A};{z_A})\) và \(B({x_B};{y_B};{z_B})\).
a) Vectơ \(\overrightarrow {AB} \) có phải là một vectơ chỉ phương của \(d\) không? Vì sao?
b) Viết phương trình tham số của đường thẳng \(d\).
c) Giả sử \({x_B} \ne {x_A},{y_B} \ne {y_A}\) và \({z_B} \ne {z_A}\), hãy viết phương trình chính tắc của \(d\).
Phương pháp giải:
a) Tìm vectơ \(\overrightarrow {AB} \), sau đó xác định xem vectơ này có phải là vectơ chỉ phương của đường thẳng \(d\).
b) Sử dụng tọa độ của điểm \(A\) hoặc \(B\) và vectơ chỉ phương \(\overrightarrow {AB} \) để viết phương trình tham số của đường thẳng.
c) Sử dụng tỉ số giữa các tọa độ và vectơ chỉ phương để viết phương trình chính tắc của đường thẳng d.
Lời giải chi tiết:
a) Vectơ \(\overrightarrow {AB} \) là vectơ chỉ phương của đường thẳng \(d\):
Vectơ \(\overrightarrow {AB} \) được xác định bởi:
\(\overrightarrow {AB} = ({x_B} - {x_A},{y_B} - {y_A},{z_B} - {z_A})\)
Hai điểm A, B đều thuộc đường thẳng d nên vectơ \(\overrightarrow {AB} \) cũng nằm trên đường thẳng d. Suy ra \(\overrightarrow {AB} \) là vectơ chỉ phương của đường thẳng \(d\).
b) Viết phương trình tham số của đường thẳng \(d\):
Phương trình tham số của đường thẳng \(d\) đi qua \(A({x_A};{y_A};{z_A})\) và có vectơ chỉ phương \(\overrightarrow {AB} = ({x_B} - {x_A},{y_B} - {y_A},{z_B} - {z_A})\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_A} + ({x_B} - {x_A})t}\\{y = {y_A} + ({y_B} - {y_A})t}\\{z = {z_A} + ({z_B} - {z_A})t}\end{array}} \right.\quad (t \in \mathbb{R})\)
c) Viết phương trình chính tắc của đường thẳng \(d\):
Giả sử \({x_A} \ne {x_B},{y_A} \ne {y_B},{z_A} \ne {z_B}\), phương trình chính tắc của đường thẳng \(d\) là:
\(\frac{{x - {x_A}}}{{{x_B} - {x_A}}} = \frac{{y - {y_A}}}{{{y_B} - {y_A}}} = \frac{{z - {z_A}}}{{{z_B} - {z_A}}}\)
Trả lời câu hỏi Luyện tập 4 trang 59 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho tam giác OAB với \(A(2; - 3;4)\), \(B( - 4;5;0)\). Viết phương trình tham số và phương trình chính tắc (nếu có) của đường thẳng AB và đường thẳng chứa đường trung tuyến kẻ từ O của tam giác OAB.
Phương pháp giải:
- Xác định vectơ chỉ phương của đường thẳng AB, chính là vectơ \(\overrightarrow {AB} \). Viết phương trình tham số của đường thẳng AB dựa trên điểm A hoặc B và vectơ chỉ phương \(\overrightarrow {AB} \). Từ phương trình tham số, lập phương trình chính tắc của đường thẳng AB.
- Xác định trung điểm M của đoạn thẳng AB. Viết phương trình đường thẳng đi qua O và M dựa trên tọa độ hai điểm này.
Lời giải chi tiết:
Xác định vectơ chỉ phương của đường thẳng AB:
\(\overrightarrow {AB} = B - A = ( - 4 - 2;5 + 3;0 - 4) = ( - 6;8; - 4)\)
Phương trình tham số của đường thẳng AB đi qua điểm \(A(2; - 3;4)\) và có vectơ chỉ phương \(( - 6;8; - 4)\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 2 - 6t}\\{y = - 3 + 8t}\\{z = 4 - 4t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Phương trình chính tắc của đường thẳng AB là:
\(\frac{{x - 2}}{{ - 6}} = \frac{{y + 3}}{8} = \frac{{z - 4}}{{ - 4}}\)
Trung điểm M của đoạn AB có tọa độ:
\(M = \left( {\frac{{2 + ( - 4)}}{2};\frac{{ - 3 + 5}}{2};\frac{{4 + 0}}{2}} \right) = ( - 1;1;2)\)
Phương trình tham số của đường thẳng đi qua \(O(0;0;0)\) và \(M( - 1;1;2)\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = - t}\\{y = t}\\{z = 2t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Phương trình chính tắc của đường thẳng là:
\(\frac{x}{{ - 1}} = \frac{y}{1} = \frac{z}{2}\)
Trả lời câu hỏi Vận dụng 1 trang 59 SGK Toán 12 Cùng khám phá
Anh Bình là một nhiếp ảnh gia chuyên săn ảnh chim hoang dã. Giả sử với hệ trục Oxyz cho trước, anh Bình đang ngắm và ống kính ở vị trí A có tọa độ \((200;685;436)\) thì có một con gà lôi tía xuất hiện ở vị trí B có tọa độ \((640;550;474)\).
a) Viết phương trình tham số của đường thẳng chứa đoạn thẳng nối hai vị trí ống kính ngắm của anh Bình và con gà lôi tía.
b) Nếu một quả đồi có tọa độ đỉnh C là \((420;617,5;450)\). Hỏi C có thuộc đường ngắm AB không? Anh Bình có ngắm thấy con gà lôi tía này không?
Phương pháp giải:
a) Xác định vectơ chỉ phương của đường thẳng AB. Viết phương trình tham số của đường thẳng AB.
b) Thay toạ độ C vào phương trình tham số của đường thẳng AB. Xác định giá trị tham số t và kiểm tra xem các tọa độ của C có thỏa mãn không.
Lời giải chi tiết:
a) Vectơ chỉ phương của đường thẳng AB là:
\(\overrightarrow {AB} = (640 - 200;550 - 685;474 - 436) = (440; - 135;38)\)
Phương trình tham số của đường thẳng AB đi qua điểm \(A(200;685;436)\) và có vectơ chỉ phương \(\overrightarrow {AB} = (440; - 135;38)\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 200 + 440t}\\{y = 685 - 135t}\\{z = 436 + 38t}\end{array}} \right.\quad (t \in \mathbb{R})\)
b) Thay tọa độ của \(C\) vào phương trình tham số:
\(\left\{ {\begin{array}{*{20}{l}}{420 = 200 + 440t}\\{617.5 = 685 - 135t}\\{450 = 436 + 38t}\end{array}} \right.\)
Giải phương trình:
\(t = \frac{{420 - 200}}{{440}} = \frac{{220}}{{440}} = 0.5\)
\(t = \frac{{685 - 617.5}}{{135}} = \frac{{67.5}}{{135}} = 0.5\)
\(t = \frac{{450 - 436}}{{38}} = \frac{{14}}{{38}} \approx 0.368\)
Kết luận: Giá trị \(t\) không giống nhau cho cả ba phương trình, do đó điểm \(C\) không thuộc đường thẳng AB. Và vì \(450 < 436 + 38.0,5 = 455\) nên C thấp hơn đường thẳng AB. Vậy quả đồi không chắn tầm nhìn nên anh Bình có thể ngắm thấy con gà lôi tía này.
Trả lời câu hỏi Hoạt động 1 trang 54 SGK Toán 12 Cùng khám phá
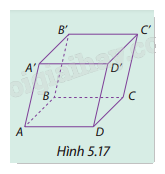
Cho hình hộp ABCD.A'B'C'D' (Hình 5.17). Tìm bốn vectơ khác \(\overrightarrow 0 \) có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp và có giá song song hoặc trùng với đường thẳng AB.
Phương pháp giải:
Tìm tất cả các cạnh song song hoặc trùng với cạnh AB.
Tìm các vectơ tương ứng với các cạnh đó, chính là các vectơ có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp.
Lời giải chi tiết:
Vectơ đầu tiên là \(\overrightarrow {AB} \).
Các cạnh song song với AB gồm: A’B’, C’D’, CD.
Các vectơ khác \(\overrightarrow 0 \)có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp và có giá song song hoặc trùng với đường thẳng AB là:
\(\overrightarrow {AB} ,\quad \overrightarrow {A'B'} ,\quad \overrightarrow {CD} ,\quad \overrightarrow {C'D'} ,\quad \overrightarrow {BA} ,\quad \overrightarrow {B'A'} ,\quad \overrightarrow {DC} ,\quad \overrightarrow {D'C'} \).
Trả lời câu hỏi Hoạt động 2 trang 55 SGK Toán 12 Cùng khám phá
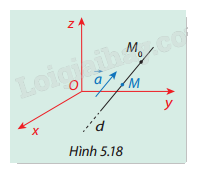
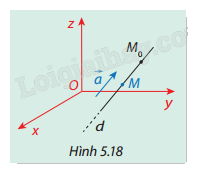
Trong không gian \(Oxyz\), cho đường thẳng \(d\) qua điểm \({M_0}({x_0};{y_0};{z_0})\), có vectơ chỉ phương \(\vec a = ({a_1};{a_2};{a_3})\). Giả sử \(M(x;y;z)\) là một điểm bất kỳ trên \(d\)(Hình 5.18). Ta biết \(\overrightarrow {{M_0}M} \) cùng phương với \(\vec a\) nên tồn tại số thực \(t\) sao cho \(\overrightarrow {{M_0}M} = t\vec a\).
a) Hãy tính tọa độ điểm \(M\) theo \({x_0},{y_0},{z_0},{a_1},{a_2},{a_3},t\).
b) Bạn An cho rằng điều kiện cần và đủ để \(M(x;y;z) \in d\) là:
\[\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\]
Bạn An phát biểu đúng hay không? Vì sao?
Phương pháp giải:
Do \(\overrightarrow {{M_0}M} = t\vec a\), ta có:
\(\overrightarrow {{M_0}M} = (x - {x_0},y - {y_0},z - {z_0}) = t({a_1},{a_2},{a_3})\)
Từ đó dẫn đến hệ phương trình:
\(x = {x_0} + t{a_1},\,\,y = {y_0} + t{a_2},\,\,z = {z_0} + t{a_3}\)
Lời giải chi tiết:
a)
Do \(\overrightarrow {{M_0}M} = t\vec a\), ta có:
\(\overrightarrow {{M_0}M} = (x - {x_0},y - {y_0},z - {z_0}) = t({a_1},{a_2},{a_3})\)
Dẫn đến hệ phương trình:
\(x = {x_0} + t{a_1},\,\,y = {y_0} + t{a_2},\,\,z = {z_0} + t{a_3}\)
Vậy tọa độ của điểm \(M\) là:
\(M({x_0} + t{a_1},{y_0} + t{a_2},{z_0} + t{a_3})\)
b)
Vì d và \({M_0}M\) đều cùng song song với giá của vectơ \(\overrightarrow a \) nên d và \({M_0}M\) song song hoặc trùng nhau.
Mặt khác \({M_0} \in d\) suy ra \(M \in d\).
Vậy phát biểu của bạn An là đúng. Điều kiện để \(M(x,y,z) \in d\) là tồn tại t sao cho hệ phương trình tham số:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + t{a_1}}\\{y = {y_0} + t{a_2}}\\{z = {z_0} + t{a_3}}\end{array}} \right.\)
được thoả mãn.
Trả lời câu hỏi Luyện tập 1 trang 55 SGK Toán 12 Cùng khám phá
Cho hình chóp S.ABCD với ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAB) và (SCD). Tìm các vectơ có điểm đầu và điểm cuối trong các điểm S, A, B, C, D đã cho và là vectơ chỉ phương của d.
Phương pháp giải:
Sử dụng định nghĩa của vectơ chỉ phương: “Cho đường thẳng d, một vecto \(\overrightarrow u \)được gọi là VTCP của đường thẳng d nếu \(\overrightarrow u \) có giá song song hoặc trùng với đường thẳng d.”
Lời giải chi tiết:
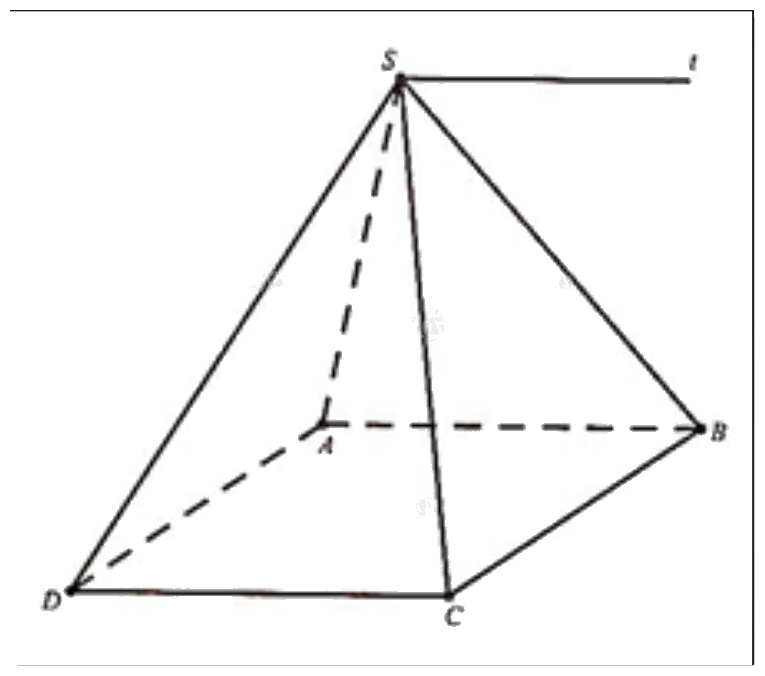
Từ hình vẽ ta thấy đường thẳng d song song với hai cạnh đáy AB và CD.
Suy ra vectơ chỉ phương của d là: \(\overrightarrow {AB} ,\,\,\overrightarrow {BA} ,\,\,\overrightarrow {CD} ,\,\,\overrightarrow {DC} \).
Trả lời câu hỏi Hoạt động 1 trang 54 SGK Toán 12 Cùng khám phá
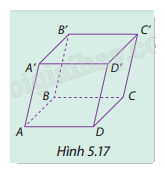
Cho hình hộp ABCD.A'B'C'D' (Hình 5.17). Tìm bốn vectơ khác \(\overrightarrow 0 \) có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp và có giá song song hoặc trùng với đường thẳng AB.
Phương pháp giải:
Tìm tất cả các cạnh song song hoặc trùng với cạnh AB.
Tìm các vectơ tương ứng với các cạnh đó, chính là các vectơ có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp.
Lời giải chi tiết:
Vectơ đầu tiên là \(\overrightarrow {AB} \).
Các cạnh song song với AB gồm: A’B’, C’D’, CD.
Các vectơ khác \(\overrightarrow 0 \)có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp và có giá song song hoặc trùng với đường thẳng AB là:
\(\overrightarrow {AB} ,\quad \overrightarrow {A'B'} ,\quad \overrightarrow {CD} ,\quad \overrightarrow {C'D'} ,\quad \overrightarrow {BA} ,\quad \overrightarrow {B'A'} ,\quad \overrightarrow {DC} ,\quad \overrightarrow {D'C'} \).
Trả lời câu hỏi Luyện tập 1 trang 55 SGK Toán 12 Cùng khám phá
Cho hình chóp S.ABCD với ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAB) và (SCD). Tìm các vectơ có điểm đầu và điểm cuối trong các điểm S, A, B, C, D đã cho và là vectơ chỉ phương của d.
Phương pháp giải:
Sử dụng định nghĩa của vectơ chỉ phương: “Cho đường thẳng d, một vecto \(\overrightarrow u \)được gọi là VTCP của đường thẳng d nếu \(\overrightarrow u \) có giá song song hoặc trùng với đường thẳng d.”
Lời giải chi tiết:
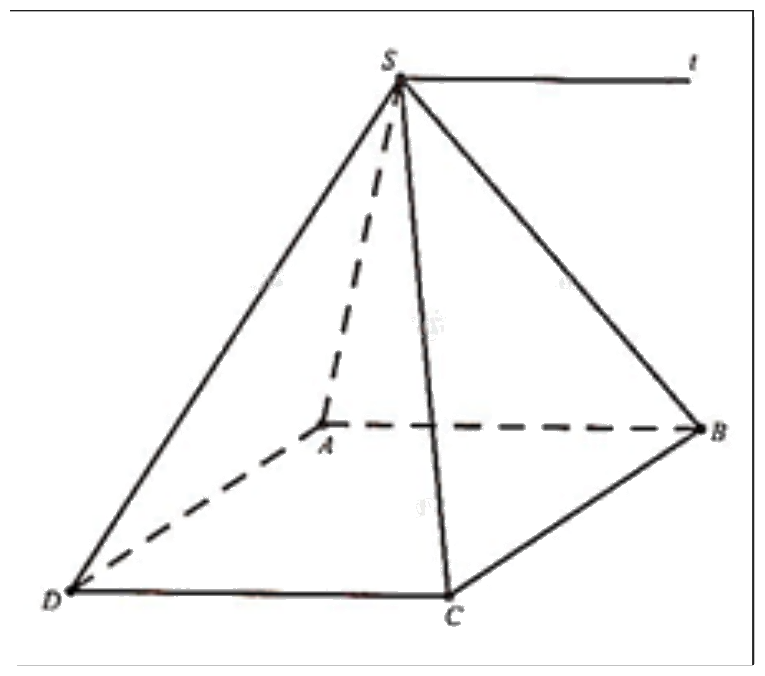
Từ hình vẽ ta thấy đường thẳng d song song với hai cạnh đáy AB và CD.
Suy ra vectơ chỉ phương của d là: \(\overrightarrow {AB} ,\,\,\overrightarrow {BA} ,\,\,\overrightarrow {CD} ,\,\,\overrightarrow {DC} \).
Trả lời câu hỏi Hoạt động 2 trang 55 SGK Toán 12 Cùng khám phá
Trong không gian \(Oxyz\), cho đường thẳng \(d\) qua điểm \({M_0}({x_0};{y_0};{z_0})\), có vectơ chỉ phương \(\vec a = ({a_1};{a_2};{a_3})\). Giả sử \(M(x;y;z)\) là một điểm bất kỳ trên \(d\)(Hình 5.18). Ta biết \(\overrightarrow {{M_0}M} \) cùng phương với \(\vec a\) nên tồn tại số thực \(t\) sao cho \(\overrightarrow {{M_0}M} = t\vec a\).
a) Hãy tính tọa độ điểm \(M\) theo \({x_0},{y_0},{z_0},{a_1},{a_2},{a_3},t\).
b) Bạn An cho rằng điều kiện cần và đủ để \(M(x;y;z) \in d\) là:
\[\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\]
Bạn An phát biểu đúng hay không? Vì sao?
Phương pháp giải:
Do \(\overrightarrow {{M_0}M} = t\vec a\), ta có:
\(\overrightarrow {{M_0}M} = (x - {x_0},y - {y_0},z - {z_0}) = t({a_1},{a_2},{a_3})\)
Từ đó dẫn đến hệ phương trình:
\(x = {x_0} + t{a_1},\,\,y = {y_0} + t{a_2},\,\,z = {z_0} + t{a_3}\)
Lời giải chi tiết:
a)
Do \(\overrightarrow {{M_0}M} = t\vec a\), ta có:
\(\overrightarrow {{M_0}M} = (x - {x_0},y - {y_0},z - {z_0}) = t({a_1},{a_2},{a_3})\)
Dẫn đến hệ phương trình:
\(x = {x_0} + t{a_1},\,\,y = {y_0} + t{a_2},\,\,z = {z_0} + t{a_3}\)
Vậy tọa độ của điểm \(M\) là:
\(M({x_0} + t{a_1},{y_0} + t{a_2},{z_0} + t{a_3})\)
b)
Vì d và \({M_0}M\) đều cùng song song với giá của vectơ \(\overrightarrow a \) nên d và \({M_0}M\) song song hoặc trùng nhau.
Mặt khác \({M_0} \in d\) suy ra \(M \in d\).
Vậy phát biểu của bạn An là đúng. Điều kiện để \(M(x,y,z) \in d\) là tồn tại t sao cho hệ phương trình tham số:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + t{a_1}}\\{y = {y_0} + t{a_2}}\\{z = {z_0} + t{a_3}}\end{array}} \right.\)
được thoả mãn.
Trả lời câu hỏi Luyện tập 2 trang 56 SGK Toán 12 Cùng khám phá
Trong không gian \(Oxyz\), cho đường thẳng \(d\) đi qua \(A(6; - 2;3)\) và có vectơ chỉ phương \(\vec a = (2;2; - 1)\).
a) Viết phương trình tham số của \(d\).
b) Tìm điểm \(M\) thuộc \(d\) biết \(OM = 7\).
Phương pháp giải:
a) Đường thẳng \(d\) đi qua điểm \(A(6; - 2;3)\) và có vectơ chỉ phương \(\vec a = (2;2; - 1)\). Phương trình tham số của đường thẳng \(d\) có dạng:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\)
Với \({M_0} = A(6; - 2;3)\) và \(\vec a = (2;2; - 1)\), thay vào ta được phương trình tham số của \(d\).
b) Tọa độ của \(M\) được biểu diễn theo tham số \(t\) từ phương trình tham số của \(d\). Dùng điều kiện \(OM = 7\), tức là khoảng cách từ gốc tọa độ \(O(0;0;0)\) đến \(M\), ta có:
\(OM = \sqrt {{x^2} + {y^2} + {z^2}} = 7\)
Thay các tọa độ của \(M(x(t),y(t),z(t))\) từ phương trình tham số vào, rồi giải phương trình để tìm \(t\), từ đó suy ra tọa độ của \(M\).
Lời giải chi tiết:
a)
Đường thẳng \(d\) đi qua điểm \(A(6; - 2;3)\) và có vectơ chỉ phương \(\vec a = (2;2; - 1)\). Phương trình tham số của đường thẳng \(d\) có dạng:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Với \(A(6; - 2;3)\) và \(\vec a = (2;2; - 1)\), phương trình tham số của đường thẳng \(d\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 6 + 2t}\\{y = - 2 + 2t}\\{z = 3 - t}\end{array}} \right.\quad (t \in \mathbb{R})\)
b)
Điểm \(M\) có tọa độ \((x,y,z)\) thuộc đường thẳng \(d\), nên tọa độ của \(M\) được biểu diễn theo tham số \(t\) như sau:
\(M(6 + 2t, - 2 + 2t,3 - t)\)
Điều kiện \(OM = 7\) nghĩa là khoảng cách từ gốc tọa độ \(O(0;0;0)\) đến \(M\) bằng 7:
\(OM = \sqrt {{x^2} + {y^2} + {z^2}} = 7\)
Thay tọa độ của \(M\) vào phương trình khoảng cách:
\(OM = \sqrt {{{(6 + 2t)}^2} + {{( - 2 + 2t)}^2} + {{(3 - t)}^2}} = 7\)
Bình phương hai vế:
\({(6 + 2t)^2} + {( - 2 + 2t)^2} + {(3 - t)^2} = 49\)
\({(6 + 2t)^2} = 36 + 24t + 4{t^2}\)
\({( - 2 + 2t)^2} = 4 - 8t + 4{t^2}\)
\({(3 - t)^2} = 9 - 6t + {t^2}\)
\((36 + 24t + 4{t^2}) + (4 - 8t + 4{t^2}) + (9 - 6t + {t^2}) = 49\)
\(49 + 10t + 9{t^2} = 49\)
\(10t + 9{t^2} = 0\)
\(t(9t + 10) = 0\)
Do đó, ta có hai nghiệm: \(t = 0\) và \(t = - \frac{{10}}{9}\)
Với \(t = 0\), tọa độ của \(M\) là:
\(M(6 + 2 \cdot 0, - 2 + 2 \cdot 0,3 - 0) = M(6, - 2,3)\)
Với \(t = - \frac{{10}}{9}\), tọa độ của \(M\) là:
\(M\left( {6 + 2 \cdot \left( { - \frac{{10}}{9}} \right), - 2 + 2 \cdot \left( { - \frac{{10}}{9}} \right),3 - \left( { - \frac{{10}}{9}} \right)} \right)\)
\(M\left( {6 - \frac{{20}}{9}, - 2 - \frac{{20}}{9},3 + \frac{{10}}{9}} \right) = M\left( {\frac{{54}}{9} - \frac{{20}}{9},\frac{{ - 18}}{9} - \frac{{20}}{9},\frac{{27}}{9} + \frac{{10}}{9}} \right)\)
\(M\left( {\frac{{34}}{9},\frac{{ - 38}}{9},\frac{{37}}{9}} \right)\)
Trả lời câu hỏi Hoạt động 3 trang 56 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho đường thẳng \(d\) qua \({M_0}({x_0};{y_0};{z_0})\) có vectơ chỉ phương \(\vec a = ({a_1};{a_2};{a_3})\). Phương trình tham số của đường thẳng là:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Giả sử \({a_1},{a_2},{a_3}\) đều khác 0. Hãy tính các tỉ số \(\frac{{x - {x_0}}}{{{a_1}}},\frac{{y - {y_0}}}{{{a_2}}},\frac{{z - {z_0}}}{{{a_3}}}\) theo \(t\) và so sánh các tỉ số này.
Phương pháp giải:
Tính các tỉ số \(\frac{{x - {x_0}}}{{{a_1}}},\frac{{y - {y_0}}}{{{a_2}}},\frac{{z - {z_0}}}{{{a_3}}}\) theo \(t\) và so sánh các tỉ số này.
Lời giải chi tiết:
Từ phương trình tham số:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\)
Ta có:
\(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}} = t\)
Các tỉ số này đều bằng \(t\), điều này chứng tỏ tất cả các tỉ số này bằng nhau, và đường thẳng \(d\) có thể viết dưới dạng phương trình chính tắc:
\(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}}\)
Trả lời câu hỏi Luyện tập 3 trang 58 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho đường thẳng \(d\) đi qua điểm \(N( - 2;3;1)\), có vectơ chỉ phương \(\vec a = (3; - 4;5)\).
a) Viết phương trình chính tắc của đường thẳng \(d\).
b) Tìm điểm \(A\) thuộc \(d\) biết \(A\) có hoành độ bằng 4.
Phương pháp giải:
a) Viết phương trình chính tắc của đường thẳng: Dựa vào phương trình tham số của đường thẳng và các tỉ số giữa tọa độ của điểm trên đường thẳng với tọa độ của điểm qua và các thành phần của vectơ chỉ phương.
b) Tìm điểm thuộc đường thẳng: Sử dụng điều kiện hoành độ của A để tìm tham số \(t\) trong phương trình tham số của đường thẳng. Từ đó tính ra tọa độ của điểm cần tìm.
Lời giải chi tiết:
a) Viết phương trình chính tắc của đường thẳng \(d\):
Phương trình tham số của đường thẳng \(d\) có dạng:
\(\left\{ {\begin{array}{*{20}{l}}{x = - 2 + 3t}\\{y = 3 - 4t}\\{z = 1 + 5t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Phương trình chính tắc của đường thẳng \(d\) là:
\(\frac{{x + 2}}{3} = \frac{{y - 3}}{{ - 4}} = \frac{{z - 1}}{5}\)
b) Tìm điểm \(A\) thuộc \(d\) biết hoành độ của A là 4:
Điểm \(A\) thuộc \(d\) có tọa độ \(A(4;y;z)\).
Suy ra: \(t = \frac{{4 + 2}}{3} = 2\)
\(y = 3 - 4.2 = - 5\) và \(z = 1 + 5.2 = 11\)
Vậy điểm A có toạ độ là \(A(4; - 5;11)\)
Trả lời câu hỏi Hoạt động 4 trang 58 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho đường thẳng \(d\) qua hai điểm phân biệt \(A({x_A};{y_A};{z_A})\) và \(B({x_B};{y_B};{z_B})\).
a) Vectơ \(\overrightarrow {AB} \) có phải là một vectơ chỉ phương của \(d\) không? Vì sao?
b) Viết phương trình tham số của đường thẳng \(d\).
c) Giả sử \({x_B} \ne {x_A},{y_B} \ne {y_A}\) và \({z_B} \ne {z_A}\), hãy viết phương trình chính tắc của \(d\).
Phương pháp giải:
a) Tìm vectơ \(\overrightarrow {AB} \), sau đó xác định xem vectơ này có phải là vectơ chỉ phương của đường thẳng \(d\).
b) Sử dụng tọa độ của điểm \(A\) hoặc \(B\) và vectơ chỉ phương \(\overrightarrow {AB} \) để viết phương trình tham số của đường thẳng.
c) Sử dụng tỉ số giữa các tọa độ và vectơ chỉ phương để viết phương trình chính tắc của đường thẳng d.
Lời giải chi tiết:
a) Vectơ \(\overrightarrow {AB} \) là vectơ chỉ phương của đường thẳng \(d\):
Vectơ \(\overrightarrow {AB} \) được xác định bởi:
\(\overrightarrow {AB} = ({x_B} - {x_A},{y_B} - {y_A},{z_B} - {z_A})\)
Hai điểm A, B đều thuộc đường thẳng d nên vectơ \(\overrightarrow {AB} \) cũng nằm trên đường thẳng d. Suy ra \(\overrightarrow {AB} \) là vectơ chỉ phương của đường thẳng \(d\).
b) Viết phương trình tham số của đường thẳng \(d\):
Phương trình tham số của đường thẳng \(d\) đi qua \(A({x_A};{y_A};{z_A})\) và có vectơ chỉ phương \(\overrightarrow {AB} = ({x_B} - {x_A},{y_B} - {y_A},{z_B} - {z_A})\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_A} + ({x_B} - {x_A})t}\\{y = {y_A} + ({y_B} - {y_A})t}\\{z = {z_A} + ({z_B} - {z_A})t}\end{array}} \right.\quad (t \in \mathbb{R})\)
c) Viết phương trình chính tắc của đường thẳng \(d\):
Giả sử \({x_A} \ne {x_B},{y_A} \ne {y_B},{z_A} \ne {z_B}\), phương trình chính tắc của đường thẳng \(d\) là:
\(\frac{{x - {x_A}}}{{{x_B} - {x_A}}} = \frac{{y - {y_A}}}{{{y_B} - {y_A}}} = \frac{{z - {z_A}}}{{{z_B} - {z_A}}}\)
Trả lời câu hỏi Luyện tập 4 trang 59 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho tam giác OAB với \(A(2; - 3;4)\), \(B( - 4;5;0)\). Viết phương trình tham số và phương trình chính tắc (nếu có) của đường thẳng AB và đường thẳng chứa đường trung tuyến kẻ từ O của tam giác OAB.
Phương pháp giải:
- Xác định vectơ chỉ phương của đường thẳng AB, chính là vectơ \(\overrightarrow {AB} \). Viết phương trình tham số của đường thẳng AB dựa trên điểm A hoặc B và vectơ chỉ phương \(\overrightarrow {AB} \). Từ phương trình tham số, lập phương trình chính tắc của đường thẳng AB.
- Xác định trung điểm M của đoạn thẳng AB. Viết phương trình đường thẳng đi qua O và M dựa trên tọa độ hai điểm này.
Lời giải chi tiết:
Xác định vectơ chỉ phương của đường thẳng AB:
\(\overrightarrow {AB} = B - A = ( - 4 - 2;5 + 3;0 - 4) = ( - 6;8; - 4)\)
Phương trình tham số của đường thẳng AB đi qua điểm \(A(2; - 3;4)\) và có vectơ chỉ phương \(( - 6;8; - 4)\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 2 - 6t}\\{y = - 3 + 8t}\\{z = 4 - 4t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Phương trình chính tắc của đường thẳng AB là:
\(\frac{{x - 2}}{{ - 6}} = \frac{{y + 3}}{8} = \frac{{z - 4}}{{ - 4}}\)
Trung điểm M của đoạn AB có tọa độ:
\(M = \left( {\frac{{2 + ( - 4)}}{2};\frac{{ - 3 + 5}}{2};\frac{{4 + 0}}{2}} \right) = ( - 1;1;2)\)
Phương trình tham số của đường thẳng đi qua \(O(0;0;0)\) và \(M( - 1;1;2)\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = - t}\\{y = t}\\{z = 2t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Phương trình chính tắc của đường thẳng là:
\(\frac{x}{{ - 1}} = \frac{y}{1} = \frac{z}{2}\)
Trả lời câu hỏi Vận dụng 1 trang 59 SGK Toán 12 Cùng khám phá
Anh Bình là một nhiếp ảnh gia chuyên săn ảnh chim hoang dã. Giả sử với hệ trục Oxyz cho trước, anh Bình đang ngắm và ống kính ở vị trí A có tọa độ \((200;685;436)\) thì có một con gà lôi tía xuất hiện ở vị trí B có tọa độ \((640;550;474)\).
a) Viết phương trình tham số của đường thẳng chứa đoạn thẳng nối hai vị trí ống kính ngắm của anh Bình và con gà lôi tía.
b) Nếu một quả đồi có tọa độ đỉnh C là \((420;617,5;450)\). Hỏi C có thuộc đường ngắm AB không? Anh Bình có ngắm thấy con gà lôi tía này không?
Phương pháp giải:
a) Xác định vectơ chỉ phương của đường thẳng AB. Viết phương trình tham số của đường thẳng AB.
b) Thay toạ độ C vào phương trình tham số của đường thẳng AB. Xác định giá trị tham số t và kiểm tra xem các tọa độ của C có thỏa mãn không.
Lời giải chi tiết:
a) Vectơ chỉ phương của đường thẳng AB là:
\(\overrightarrow {AB} = (640 - 200;550 - 685;474 - 436) = (440; - 135;38)\)
Phương trình tham số của đường thẳng AB đi qua điểm \(A(200;685;436)\) và có vectơ chỉ phương \(\overrightarrow {AB} = (440; - 135;38)\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 200 + 440t}\\{y = 685 - 135t}\\{z = 436 + 38t}\end{array}} \right.\quad (t \in \mathbb{R})\)
b) Thay tọa độ của \(C\) vào phương trình tham số:
\(\left\{ {\begin{array}{*{20}{l}}{420 = 200 + 440t}\\{617.5 = 685 - 135t}\\{450 = 436 + 38t}\end{array}} \right.\)
Giải phương trình:
\(t = \frac{{420 - 200}}{{440}} = \frac{{220}}{{440}} = 0.5\)
\(t = \frac{{685 - 617.5}}{{135}} = \frac{{67.5}}{{135}} = 0.5\)
\(t = \frac{{450 - 436}}{{38}} = \frac{{14}}{{38}} \approx 0.368\)
Kết luận: Giá trị \(t\) không giống nhau cho cả ba phương trình, do đó điểm \(C\) không thuộc đường thẳng AB. Và vì \(450 < 436 + 38.0,5 = 455\) nên C thấp hơn đường thẳng AB. Vậy quả đồi không chắn tầm nhìn nên anh Bình có thể ngắm thấy con gà lôi tía này.
Mục 1 của SGK Toán 12 tập 2 thường xoay quanh các chủ đề về đạo hàm của hàm số, ứng dụng đạo hàm để khảo sát hàm số và các bài toán liên quan đến cực trị, giá trị lớn nhất, giá trị nhỏ nhất. Việc nắm vững các khái niệm và kỹ năng giải toán trong mục này là vô cùng quan trọng để đạt kết quả tốt trong các kỳ thi sắp tới.
Dưới đây là phần giải chi tiết các bài tập trong Mục 1, trang 54, 55, 56, 57, 58, 59 SGK Toán 12 tập 2:
Để giải các bài tập về đạo hàm và ứng dụng đạo hàm một cách hiệu quả, các em cần:
Ngoài SGK, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với những hướng dẫn chi tiết trên, các em sẽ tự tin hơn trong việc giải các bài tập Mục 1 trang 54, 55, 56, 57, 58, 59 SGK Toán 12 tập 2. Chúc các em học tốt!