Khảo sát và vẽ đồ thị hàm số là một trong những chủ đề quan trọng bậc nhất trong chương trình Toán 12. Việc nắm vững lý thuyết và kỹ năng thực hành sẽ giúp học sinh giải quyết các bài toán một cách nhanh chóng và chính xác.
Tại giaitoan.edu.vn, chúng tôi cung cấp một hệ thống bài giảng chi tiết, dễ hiểu, cùng với các bài tập đa dạng, giúp bạn tiếp cận và chinh phục chủ đề này một cách hiệu quả.
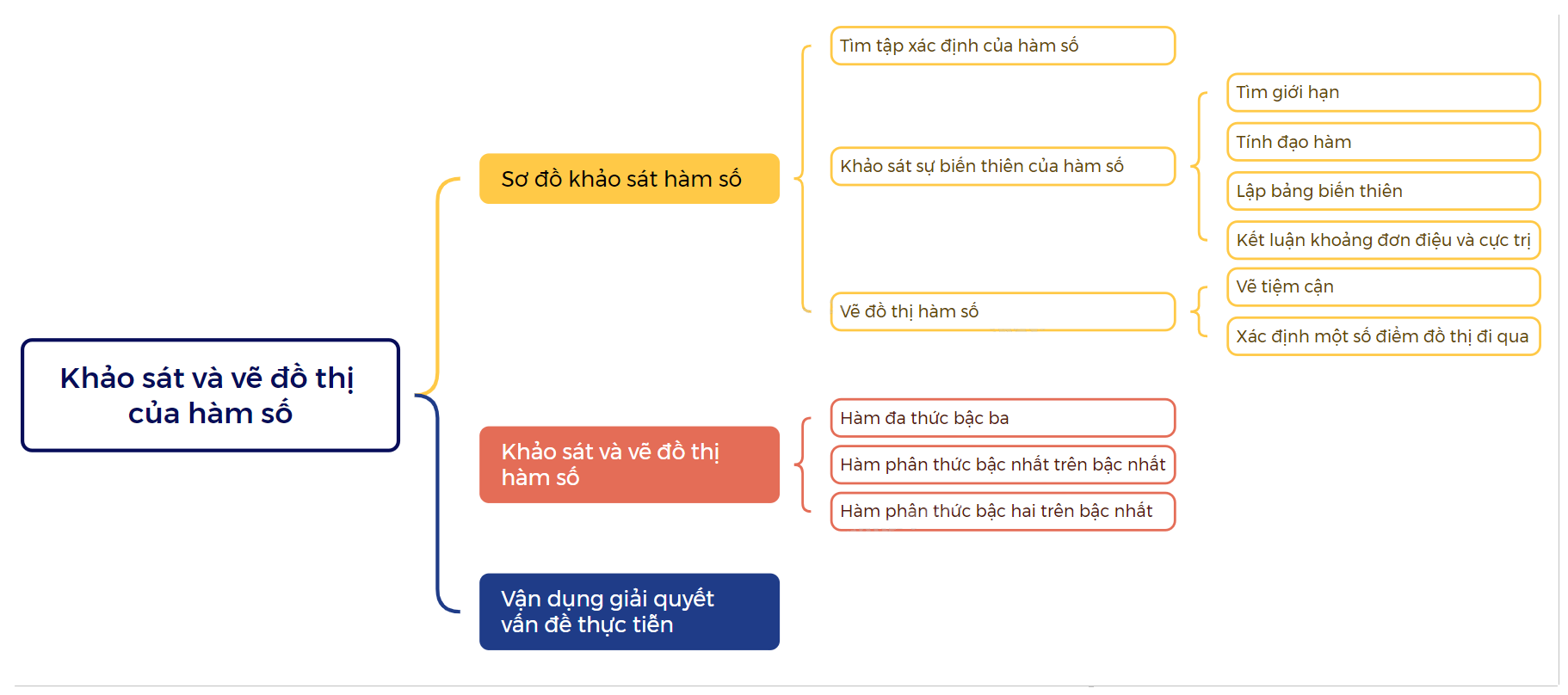
1. Sơ đồ khảo sát hàm số
1. Sơ đồ khảo sát hàm số
1. Tìm tập xác định của hàm số. 2. Khảo sát sự biến thiên của hàm số. - Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận (nếu có). - Lập BBT của hàm số bao gồm: tìm đạo hàm của hàm số, xét dấu đạo hàm, mô tả chiều biến thiên và cực trị của hàm số (nếu có), điền đầy đủ các kết quả vào bảng. - Dựa vào bảng, ta có kết luận về chiều biến thiên và cực trị. 3. Vẽ đồ thị hàm số. - Vẽ các đường tiệm cận của đồ thị (nếu có). - Xác định thêm một số điểm đặc biệt của đồ thị, chẳng hạn tìm giao điểm của đồ thị với các trục tọa độ (nếu đồ thị không cắt các trục tọa độ hoặc việc tìm các tọa độ giao điểm phức tạp thì bỏ qua phần này). - Dựa vào bảng biến thiên và các yếu tố xác định ở trên để vẽ đồ thị. |
2. Khảo sát và vẽ đồ thị hàm số \(y = a{x^3} + b{x^2} + cx + d (a \ne 0)\)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = - {x^3} + 3{x^2} - 4\).
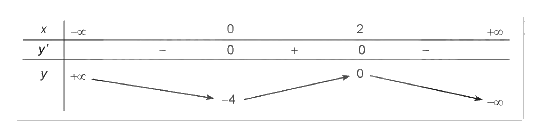
Tập xác định của hàm số: R.
Sự biến thiên:
Ta có: \(y' = - 3{x^2} + 6x\). Vậy y’ = 0 khi x = 0 hoặc x = 2
Trên khoảng \(\left( {0;2} \right)\), y’ > 0 nên hàm số đồng biến. Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\), y’ < 0 nên hàm số nghịch biến trên mỗi khoảng đó.
Hàm số đạt cực tiểu tại x = 0, giá trị cực tiểu \({y_{CT}} = - 4\). Hàm số đạt cực đại tại x = 2, giá trị cực đại.
Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = - \infty \).
BBT:
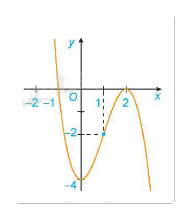
Đồ thị:
Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0;4} \right)\).
Ta có: y = 0 \( \Leftrightarrow \)x = -1 hoặc x = 2. Do đó giao điểm của đồ thị hàm số với trục hoành là các điểm \(\left( { - 1;0} \right)\) và \(\left( {2;0} \right)\).
Đồ thị hàm số có tâm đối xứng là điểm \(\left( {1; - 2} \right)\).
3. Khảo sát và vẽ đồ thị hàm số\(y = \frac{{ax + b}}{{cx + d}}(c \ne 0,ad - bc \ne 0)\)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{x + 1}}{{x - 2}}\).
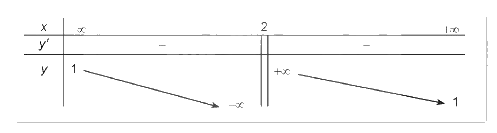
Tập xác định của hàm số: R\{2}.
Sự biến thiên:
Ta có: \(y' = - \frac{3}{{{{(x - 2)}^2}}} < 0\) với mọi \(x \ne 2\).
Hàm số nghịch biến trên từng khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
Hàm số không có cực trị.
Tiệm cận: \(\mathop {\lim }\limits_{x \to - \infty } y = 1;\mathop {\lim }\limits_{x \to + \infty } - \infty = 1\).
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty \).
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận ngang là y = 1.
BBT:
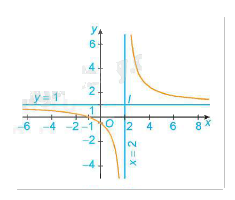
Đồ thị:
Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0; - \frac{1}{2}} \right)\).
Giao điểm của đồ thị hàm số với trục hoành là điểm \(\left( { - 1;0} \right)\).
Đồ thị hàm số nhận giao điểm I \(\left( {2;1} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng.
4. Khảo sát và vẽ đồ thịhàm số\(y = \frac{{a{x^2} + bx + c}}{{px + q}}(a \ne 0,p \ne 0)\)(đa thức tử không chia hết cho đa thức mẫu)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{{x^2} - x - 1}}{{x - 2}}\).
Tập xác định của hàm số: R\{2}.
Sự biến thiên: Viết \(y = x + 1 + \frac{1}{{x - 2}}\).
Ta có: \(y' = 1 - \frac{1}{{{{(x - 2)}^2}}} = \frac{{{x^2} - 4x + 3}}{{{{(x - 2)}^2}}}\) . Vậy y’ = 0 \( \Leftrightarrow \) x = 1 hoặc x = 3.
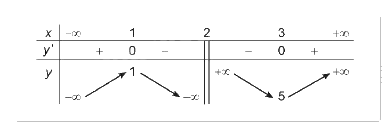
Trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\), y’ > 0 nên hàm số đồng biến trên từng khoảng này.
Trên các khoảng \(\left( {1;2} \right)\) và \(\left( {2;3} \right)\), y’ < 0 nên hàm số nghịch biến trên từng khoảng này.
Hàm số đạt cực đại tại x = 1 với ; hàm số đạt cực tiểu tại x = 3 với \({y_{CT}} = 5\).
\(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\mathop {\lim }\limits_{x \to + \infty } y = + \infty \).
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty \).
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 2}} = 0\); \(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 2}} = 0\).
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận xiên là y = x + 1.
BBT:
Đồ thị:
Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0;\frac{1}{2}} \right)\).
Ta có: \(y = 0 \Leftrightarrow x = \frac{{1 - \sqrt 5 }}{2};x = \frac{{1 + \sqrt 5 }}{2}\). Do đó giao điểm của đồ thị hàm số với trục hoành là điểm \(\left( {\frac{{1 - \sqrt 5 }}{2};0} \right);\left( {\frac{{1 + \sqrt 5 }}{2};0} \right)\).
Đồ thị hàm số nhận giao điểm I \(\left( {2;3} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng.
5. Vận dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan thực tiễn
Ví dụ: Khi một vật lạ mắc kẹt trong khí quản khiến ta phải ho, cơ hoành đẩy lên trên gây ra tăng áp lực trong phổi, theo đó cuống họng co thắt làm hẹp khí quản khiến không khí đi qua mạnh hơn. Đối với một lượng không khí bị đẩy ra trong một khoảng thời gian cố định, khí quản càng nhỏ thì luồng không khí càng đẩy ra nhanh hơn. Vận tốc luồng khí thoát ra càng cao, lực tác động lên vật càng lớn. Qua nghiên cứu một số trường hợp, người ta nhận thấy vận tốc v của luồng khí liên hệ với bán kính x của khí quản theo công thức:
\(v(x) = k({x_0} - x){x^2}\) với \(\frac{1}{2}{x_0} \le x \le {x_0}\)
trong đó k là hằng số (k > 0) và \({x_0}\) là bán kính khí quản ở trạng thái bình thường. Tìm x theo \({x_0}\) để vận tốc của luồng khí một cơn ho trong trường hợp này là lớn nhất.
Giải:
Xét hàm số \(f(x) = ({x_0} - x){x^2}\) với \({x_0}\) cố định và \(\frac{1}{2}{x_0} \le x \le {x_0}\).
Do k là hằng số nên vận tốc của luồng khí một cơn ho lớn nhất khi f(x) đạt giá trị lớn nhất.
Ta có:
\(\begin{array}{l}f(x) = - {x^3} + {x_0}{x^2};\\f'(x) = - 3{x^2} + 2{x_0}x;\\f'(x) = 0 \Leftrightarrow x = 0,x = \frac{2}{3}{x_0}\end{array}\)
BBT:
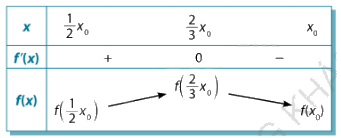
Dựa vào BBT, ta có \(\mathop {\max }\limits_{\left[ {\frac{1}{2}{x_0};{x_0}} \right]} f(x) = f\left( {\frac{2}{3}{x_0}} \right)\).
Vậy vận tốc của luồng khí một cơn ho lớn nhất khi \(x = \frac{2}{3}{x_0}\).
Chương trình Toán 12, phần khảo sát và vẽ đồ thị hàm số đóng vai trò then chốt trong việc đánh giá khả năng tư duy và vận dụng kiến thức của học sinh. Để nắm vững nội dung này, học sinh cần hiểu rõ các bước tiến hành và các khái niệm liên quan. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết khảo sát và vẽ đồ thị hàm số, giúp bạn học tập hiệu quả hơn.
Hàm số bậc ba có tính đối xứng qua điểm uốn. Việc tìm điểm uốn và các điểm cực trị là rất quan trọng để vẽ đồ thị chính xác.
Hàm số hữu tỉ thường có tiệm cận đứng và tiệm cận ngang. Việc xác định tiệm cận giúp xác định giới hạn của đồ thị hàm số.
Hàm số lượng giác có tính tuần hoàn. Việc xác định chu kỳ và các điểm đặc biệt giúp vẽ đồ thị chính xác.
Ví dụ 1: Khảo sát hàm số y = x³ - 3x² + 2x.
Ví dụ 2: Khảo sát hàm số y = (x + 1)/(x - 2).
Ví dụ 3: Khảo sát hàm số y = sin 2x.
Để học tốt phần khảo sát và vẽ đồ thị hàm số, bạn cần:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết khảo sát và vẽ đồ thị hàm số Toán 12. Chúc bạn học tập tốt!