Chào mừng các em học sinh đến với bài giải bài tập 5.14 trang 53 SGK Toán 12 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12, tập trung vào kiến thức về số phức và các phép toán liên quan.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
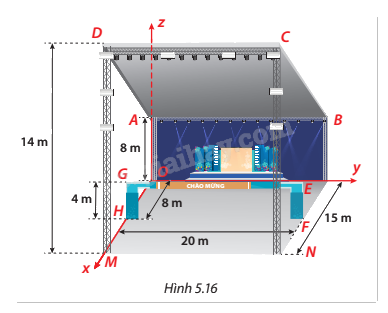
Người ta thiết kế một mái che hình chữ nhật ABCD phía trên sân khấu. a) Với hệ trục Oxyz (đơn vị trên trục là mét) và các kích thước được cho như Hình 5.16, hãy viết phương trình mặt phẳng chứa mái che. b) Một cổng chào hình chữ nhật EFHG cao 4 m dựng vuông góc với mặt đất. Người ta muốn làm các đoạn dây nối thanh ngang GE với mái che để gắn hoa và đèn led. Tính độ dài ngắn nhất của mỗi đoạn dây này.
Đề bài
Người ta thiết kế một mái che hình chữ nhật ABCD phía trên sân khấu.
a) Với hệ trục Oxyz (đơn vị trên trục là mét) và các kích thước được cho như Hình 5.16, hãy viết phương trình mặt phẳng chứa mái che.
b) Một cổng chào hình chữ nhật EFHG cao 4 m dựng vuông góc với mặt đất. Người ta muốn làm các đoạn dây nối thanh ngang GE với mái che để gắn hoa và đèn led. Tính độ dài ngắn nhất của mỗi đoạn dây này.
Phương pháp giải - Xem chi tiết
a) Xác định tọa độ các điểm A, B, C, D của mái che. Sử dụng 3 điểm để viết phương trình mặt phẳng chứa mái che. Tìm hai vectơ chỉ phương và tính tích có hướng để xác định vectơ pháp tuyến của mặt phẳng. Dùng vectơ pháp tuyến viết phương trình mặt phẳng.
b) Tìm tọa độ các điểm G, E. Tính khoảng cách từ điểm G hoặc E đến mặt phẳng chứa mái che. Sử dụng công thức khoảng cách từ một điểm đến mặt phẳng để tính độ dài ngắn nhất của đoạn dây.
Lời giải chi tiết
a)
Giả sử tọa độ các điểm của mái che là:
\(A(0;0;8),\quad B(0;20;8),\quad C(15;20;14),\quad D(15;0;14).\)
Các điểm này nằm trên mặt phẳng chứa mái che. Tính hai vectơ chỉ phương:
\(\overrightarrow {AB} = (0;20;0),\quad \overrightarrow {AC} = (15;20;6).\)
Tích có hướng của hai vectơ:
\(\vec n = \overrightarrow {AB} \times \overrightarrow {AC} = (120;0; - 300).\)
Vectơ pháp tuyến của mặt phẳng là \(\vec n = (120;0; - 300)\). Phương trình mặt phẳng có dạng:
\(120(x - 0) + 0y - 300(z - 8) = 0\quad \Rightarrow \quad 120x - 300z + 2400 = 0\,\,\, \Leftrightarrow \,\,\,2x - 5z + 40 = 0\)
Vậy phương trình mặt phẳng chứa mái che là \(\,2x - 5z + 40 = 0\).
b)
Giả sử tọa độ các điểm \(G(0;0;4)\).
Khoảng cách từ điểm \(G(0;0;4)\) đến mặt phẳng \((ABCD)\) chính là độ dài ngắn nhất của đoạn dây nối từ thanh ngang GE với mái che được tính bằng công thức:
\(d = \frac{{|2.0 - 5.4 + 40|}}{{\sqrt {{2^2} + {{( - 5)}^2}} }} = \frac{{20}}{{\sqrt {29} }}\)
Vậy độ dài ngắn nhất của mỗi đoạn dây là \(\frac{{20}}{{\sqrt {29} }}\) mét.
Bài tập 5.14 trang 53 SGK Toán 12 tập 2 thường liên quan đến việc tìm phần thực, phần ảo của số phức, thực hiện các phép toán cộng, trừ, nhân, chia số phức, hoặc giải phương trình bậc hai với hệ số phức. Để giải quyết bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về số phức:
Ví dụ minh họa:
Giả sử bài tập yêu cầu tìm phần thực và phần ảo của số phức z = (2 + 3i)(1 - i). Ta thực hiện như sau:
Các dạng bài tập thường gặp:
Mẹo giải nhanh:
Luyện tập thêm:
Để củng cố kiến thức và kỹ năng giải bài tập về số phức, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 12 tập 2 và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học luyện thi THPT Quốc gia để được hướng dẫn chi tiết hơn.
Kết luận:
Bài tập 5.14 trang 53 SGK Toán 12 tập 2 là một bài tập quan trọng giúp các em hiểu sâu hơn về số phức và các phép toán liên quan. Bằng cách nắm vững kiến thức cơ bản, thực hành nhiều bài tập và áp dụng các mẹo giải nhanh, các em có thể tự tin giải quyết bài tập này một cách hiệu quả.
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ học tập tốt môn Toán 12 và đạt kết quả cao trong các kỳ thi sắp tới.
Các bài tập liên quan: