Chào mừng các em học sinh đến với bài giải bài tập 4.22 trang 31 SGK Toán 12 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
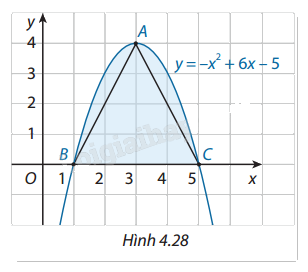
Gọi \((H)\) là hình phẳng giới hạn bởi parabol \(y = - {x^2} + 6x - 5\) và trục hoành. (Hình 4.28) a) Tính diện tích \(S\) của hình \((H)\). b) Từ thế kỉ thứ III trước Công nguyên, khi phép tính tích phân chưa ra đời, Archimedes đã dùng phương pháp của riêng mình và chỉ ra rằng diện tích của hình \((H)\) bằng \(\frac{4}{3}\) lần diện tích tam giác \(ABC\). Tính \(S\) theo kết quả mà Archimedes đã tìm ra và so sánh với kết quả ở câu a.
Đề bài
Gọi \((H)\) là hình phẳng giới hạn bởi parabol \(y = - {x^2} + 6x - 5\) và trục hoành. (Hình 4.28)
a) Tính diện tích \(S\) của hình \((H)\).
b) Từ thế kỉ thứ III trước Công nguyên, khi phép tính tích phân chưa ra đời, Archimedes đã dùng phương pháp của riêng mình và chỉ ra rằng diện tích của hình \((H)\) bằng \(\frac{4}{3}\) lần diện tích tam giác \(ABC\). Tính \(S\) theo kết quả mà Archimedes đã tìm ra và so sánh với kết quả ở câu a.
Phương pháp giải - Xem chi tiết
a)
Tính diện tích hình phẳng bằng tích phân xác định của hàm \(y = f(x)\) trên đoạn từ giao điểm của parabol với trục hoành.
Bước đầu tiên là tìm nghiệm của phương trình \[y = 0\] (giao điểm với trục hoành).
Sau đó, sử dụng tích phân xác định để tính diện tích hình phẳng.
b)
Diện tích của tam giác \(ABC\) được tính theo công thức diện tích tam giác.
Sau đó, sử dụng kết quả mà Archimedes đã chỉ ra: Diện tích hình \((H)\) bằng \(\frac{4}{3}\) lần diện tích của tam giác \(ABC\)
Lời giải chi tiết
a)
- Phương trình parabol là:
\(y = - {x^2} + 6x - 5.\)
- Tìm nghiệm của phương trình \(y = 0\):
\( - {x^2} + 6x - 5 = 0\quad \Rightarrow \quad x = 1,{\mkern 1mu} x = 5.\)
- Diện tích hình phẳng \(S\) được tính bằng tích phân:
\(S = \int_1^5 {( - {x^2} + 6x - 5)} {\mkern 1mu} dx.\)
Tính tích phân:
\(S = \left[ { - \frac{{{x^3}}}{3} + 3{x^2} - 5x} \right]_1^5 = \left( { - \frac{{125}}{3} + 50} \right) - \left( { - \frac{1}{3} - 2} \right) = \frac{{32}}{3}.\)
Vậy diện tích hình phẳng \(S = \frac{{32}}{3}\).
b)
- Diện tích tam giác \(ABC\) với \(A(3,4)\), \(B(1,0)\), và \(C(5,0)\) là:
\({S_{\Delta ABC}} = \frac{1}{2} \times 4 \times 4 = 8.\)
- Theo Archimedes, diện tích hình \((H)\) bằng \(\frac{4}{3}\) lần diện tích tam giác \(ABC\):
\(S = \frac{4}{3} \times 8 = \frac{{32}}{3}.\)
Kết quả này khớp với kết quả của câu a.
Bài tập 4.22 trang 31 SGK Toán 12 tập 2 thường liên quan đến việc ứng dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế, chẳng hạn như tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, hoặc xét tính đơn điệu của hàm số. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các bước sau:
Giả sử bài tập 4.22 yêu cầu tìm giá trị lớn nhất của hàm số f(x) = -x3 + 3x2 - 2 trên đoạn [-1; 3]. Chúng ta sẽ áp dụng các bước trên để giải quyết bài toán này:
Ngoài bài tập 4.22, SGK Toán 12 tập 2 còn nhiều bài tập tương tự liên quan đến ứng dụng đạo hàm. Các bài tập này thường yêu cầu:
Để giải quyết các bài tập này, chúng ta cần nắm vững các kiến thức về đạo hàm, điểm cực trị, khoảng đồng biến, nghịch biến và các phương pháp giải quyết bài toán tối ưu hóa.
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, các em có thể luyện tập thêm các bài tập trong SGK, sách bài tập và các đề thi thử. Ngoài ra, các em cũng có thể tham khảo các tài liệu học tập trực tuyến và các video hướng dẫn giải bài tập trên giaitoan.edu.vn.
Trong quá trình học tập và giải bài tập, các em nên:
Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!