Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Ở bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 2 trang 58, 59, 60 sách giáo khoa Toán 12 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải và tự tin làm bài tập.
Cho hình hộp ABCD.EFGH có O và P tương ứng là giao điểm các đường chéo của hai đáy ABCD và EFGH. M là trung điểm của đoạn thẳng EP (Hình 2.14). Xét mối quan hệ về hướng và độ dài của các cặp vectơ: a) \(\overrightarrow {BD} \) và \(\overrightarrow {FP} \). b) \(\overrightarrow {EM} \) và \(\overrightarrow {CA} \).
Trả lời câu hỏi Vận dụng 2 trang 59 SGK Toán 12 Cùng khám phá
Trọng lực \(\vec P\) là lực hấp dẫn do Trái Đất tác dụng lên một vật, được tính theo công thức \(\vec P = m\vec g\), trong đó \(m\) là khối lượng của vật (đơn vị: kg), còn \(\vec g\) là vectơ gia tốc rơi tự do, có hướng đi xuống và có độ lớn \(g = 9,8{\mkern 1mu} m/{s^2}\). Xác định hướng và độ lớn của trọng lực (đơn vị: N) tác dụng lên quả bưởi có khối lượng \(2,5{\mkern 1mu} kg\).
Phương pháp giải:
- Sử dụng công thức tính trọng lực: \(\vec P = m\vec g\)
- Thay các giá trị đã cho vào công thức để tính toán.
Lời giải chi tiết:
- Khối lượng của quả bưởi: \(m = 2,5{\mkern 1mu} kg\).
- Gia tốc rơi tự do: \(g = 9,8{\mkern 1mu} m/{s^2}\).
- Trọng lực tác dụng lên quả bưởi được tính theo công thức: \(P = m \cdot g\).
- Thay các giá trị vào: \(P = 2,5 \times 9,8 = 24,5{\mkern 1mu} N\).
- Hướng của trọng lực: Hướng xuống dưới (theo chiều của vectơ \(\vec g\)).
Kết luận:
- Độ lớn của trọng lực tác dụng lên quả bưởi là \(24,5{\mkern 1mu} N\).
- Hướng của trọng lực là hướng xuống dưới.
Trả lời câu hỏi Luyện tập 5 trang 60 SGK Toán 12 Cùng khám phá
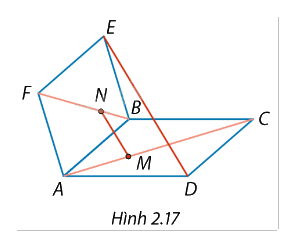
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Trên các đường chéo AC và BF lấy các điểm \(M\), \(N\) sao cho \(MC = 2MA\), \(NF = 2NB\) (Hình 2.17).
a) Biểu diễn các vectơ \(\overrightarrow {MN} \), \(\overrightarrow {DE} \) theo \(\overrightarrow {AB} \), \(\overrightarrow {AD} \), \(\overrightarrow {AF} \).
b) Từ đó suy ra MN//DE.
Phương pháp giải:
a) Áp dụng quy tắc ba điểm và quy tắc hình bình hành kết hợp với các tính chất của phép nhân một số với một vectơ.
b) Tìm k (k≠0) sao cho \(\overrightarrow {MN} = k\overrightarrow {DE} \)thì hai vectơ đó song song.
Lời giải chi tiết:
a)
Do \(MC = 2MA\), \(NF = 2NB\) nên \(\overrightarrow {AC} = - 3\overrightarrow {MA}, \overrightarrow {FB} = \frac{2}{3}\overrightarrow {FN} \).
- Biểu diễn \(\overrightarrow {MN} \)
Sử dụng quy tắc ba điểm vào \(\overrightarrow {MN} \): \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AN} = - \frac{1}{3}\overrightarrow {AC} + \overrightarrow {AF} + \frac{2}{3}\overrightarrow {FB} (*)\)
Áp dụng quy tắc hình bình hành ta có:
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(\overrightarrow {FA} + \overrightarrow {FE} = \overrightarrow {FB} \)
Thay vào (*) ta có:
\(\overrightarrow {MN} = - \frac{1}{3}(\overrightarrow {AB} + \overrightarrow {AD} ) + \overrightarrow {AF} + \frac{2}{3}(\overrightarrow {FA} + \overrightarrow {FE} ) = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {AF} + \frac{2}{3}\overrightarrow {AB} = \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {AF} \)
\(\overrightarrow {MN} = \frac{1}{3}\left( {\overrightarrow {AB} - \overrightarrow {AD} + \overrightarrow {AF} } \right)\)
- Biểu diễn \(\overrightarrow {DE} \)
Sử dụng quy tắc ba điểm vào \(\overrightarrow {DE} \):
\(\overrightarrow {DE} = \overrightarrow {DA} + \overrightarrow {AE} = - \overrightarrow {AD} + \overrightarrow {AB} + \overrightarrow {AF} \)
b) Từ câu a ta thấy \(\overrightarrow {MN} = \frac{1}{3}\overrightarrow {DE} \) suy ra MN // DE.
Trả lời câu hỏi Hoạt động 4 trang 58 SGK Toán 12 Cùng khám phá
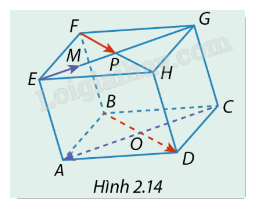
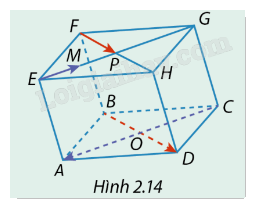
Cho hình hộp ABCD.EFGH có O và P tương ứng là giao điểm các đường chéo của hai đáy ABCD và EFGH. M là trung điểm của đoạn thẳng EP (Hình 2.14). Xét mối quan hệ về hướng và độ dài của các cặp vectơ:
a) \(\overrightarrow {BD} \) và \(\overrightarrow {FP} \).
b) \(\overrightarrow {EM} \) và \(\overrightarrow {CA} \).
Phương pháp giải:
- Kiểm tra xem hai vectơ có cùng phương hay không (cùng phương, ngược phương hay không cùng phương).
- Tính độ dài của các vectơ để so sánh.
Lời giải chi tiết:
a) Vectơ \(\overrightarrow {BD} \) và \(\overrightarrow {FP} \):
Vì ABCD.EFGH là hình hộp nên \(\overrightarrow {BD} = \overrightarrow {FH} \) (cùng hướng và có độ dài bằng nhau vì đều là đường chéo của hai đáy hình hộp).
Lại có: \(FP = \frac{1}{2}FH\)do P là trung điểm của PH nên \(\overrightarrow {FP} = \frac{1}{2}\overrightarrow {FH} \).
Suy ra: \(\overrightarrow {BD} = 2\overrightarrow {FP} \).
b) Vectơ \(\overrightarrow {EM} \) và \(\overrightarrow {CA} \):
Tương tự, vì ABCD.EFGH là hình hộp nên \(\overrightarrow {CA} = \overrightarrow {GE} \).
Lại có: \(EM = \frac{1}{2}EP = \frac{1}{4}GE\)mà \(\overrightarrow {EM} \) ngược hướng với \(\overrightarrow {GE} \) nên \(\overrightarrow {EM} = - \frac{1}{4}\overrightarrow {GE} \).
Suy ra: \(\overrightarrow {EM} = - \frac{1}{4}\overrightarrow {CA} \).
Trả lời câu hỏi Luyện tập 4 trang 59 SGK Toán 12 Cùng khám phá
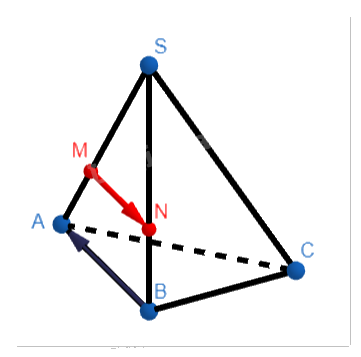
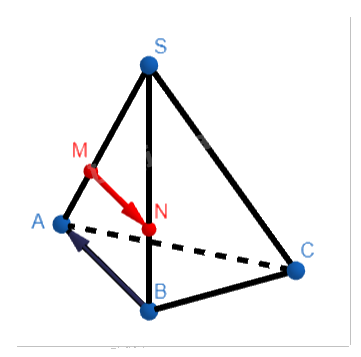
Cho hình chóp S.ABC. Điểm \(M\) thuộc cạnh SA và \(SM = \frac{2}{3}SA\).
a) Viết hệ thức liên hệ giữa các cặp vectơ \(\overrightarrow {SM} \) và \(\overrightarrow {SA} \), \(\overrightarrow {MA} \) và \(\overrightarrow {AS} \).
b) Tìm điểm \(N\) sao cho \(\overrightarrow {MN} = - \frac{2}{3}\overrightarrow {BA} \).
Phương pháp giải:
a) Sử dụng định nghĩa và tính chất của vectơ để thiết lập các mối quan hệ giữa các vectơ đã cho.
b) Sử dụng hệ thức liên quan đến vectơ để tìm tọa độ của điểm N thỏa mãn điều kiện đã cho.
Lời giải chi tiết:
a) Ta có: \(SM = \frac{2}{3}SA \Rightarrow \overrightarrow {SM} = \frac{2}{3}\overrightarrow {SA} \).
Vì \(M\) thuộc SA, nên \(MA = SA - SM\). Do đó:
\(\overrightarrow {MA} = \overrightarrow {SA} - \overrightarrow {SM} = \overrightarrow {SA} - \frac{2}{3}\overrightarrow {SA} = \frac{1}{3}\overrightarrow {SA} \).
Ta cũng có: \(\overrightarrow {AS} = - \overrightarrow {SA} \).
Suy ra: \(\overrightarrow {MA} = - \frac{1}{3}\overrightarrow {AS} \).
b) Tìm điểm \(N\) sao cho \(\overrightarrow {MN} = - \frac{2}{3}\overrightarrow {BA} \).
Ta có: \(\overrightarrow {MN} = - \frac{2}{3}\overrightarrow {BA} \to \overrightarrow {MN} = \frac{2}{3}\overrightarrow {AB} \).
Suy ra: \(MN//AB;MN = \frac{2}{3}AB\).
Tam giác SAB có đoạn thẳng MN song song với AB và \(\frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{2}{3}\) thì từ định lý Talet ta suy ra N thuộc cạnh SB:
\(\frac{{SN}}{{SB}} = \frac{2}{3} \Leftrightarrow SN = \frac{2}{3}SB\).
Trả lời câu hỏi Hoạt động 4 trang 58 SGK Toán 12 Cùng khám phá
Cho hình hộp ABCD.EFGH có O và P tương ứng là giao điểm các đường chéo của hai đáy ABCD và EFGH. M là trung điểm của đoạn thẳng EP (Hình 2.14). Xét mối quan hệ về hướng và độ dài của các cặp vectơ:
a) \(\overrightarrow {BD} \) và \(\overrightarrow {FP} \).
b) \(\overrightarrow {EM} \) và \(\overrightarrow {CA} \).
Phương pháp giải:
- Kiểm tra xem hai vectơ có cùng phương hay không (cùng phương, ngược phương hay không cùng phương).
- Tính độ dài của các vectơ để so sánh.
Lời giải chi tiết:
a) Vectơ \(\overrightarrow {BD} \) và \(\overrightarrow {FP} \):
Vì ABCD.EFGH là hình hộp nên \(\overrightarrow {BD} = \overrightarrow {FH} \) (cùng hướng và có độ dài bằng nhau vì đều là đường chéo của hai đáy hình hộp).
Lại có: \(FP = \frac{1}{2}FH\)do P là trung điểm của PH nên \(\overrightarrow {FP} = \frac{1}{2}\overrightarrow {FH} \).
Suy ra: \(\overrightarrow {BD} = 2\overrightarrow {FP} \).
b) Vectơ \(\overrightarrow {EM} \) và \(\overrightarrow {CA} \):
Tương tự, vì ABCD.EFGH là hình hộp nên \(\overrightarrow {CA} = \overrightarrow {GE} \).
Lại có: \(EM = \frac{1}{2}EP = \frac{1}{4}GE\)mà \(\overrightarrow {EM} \) ngược hướng với \(\overrightarrow {GE} \) nên \(\overrightarrow {EM} = - \frac{1}{4}\overrightarrow {GE} \).
Suy ra: \(\overrightarrow {EM} = - \frac{1}{4}\overrightarrow {CA} \).
Trả lời câu hỏi Luyện tập 4 trang 59 SGK Toán 12 Cùng khám phá
Cho hình chóp S.ABC. Điểm \(M\) thuộc cạnh SA và \(SM = \frac{2}{3}SA\).
a) Viết hệ thức liên hệ giữa các cặp vectơ \(\overrightarrow {SM} \) và \(\overrightarrow {SA} \), \(\overrightarrow {MA} \) và \(\overrightarrow {AS} \).
b) Tìm điểm \(N\) sao cho \(\overrightarrow {MN} = - \frac{2}{3}\overrightarrow {BA} \).
Phương pháp giải:
a) Sử dụng định nghĩa và tính chất của vectơ để thiết lập các mối quan hệ giữa các vectơ đã cho.
b) Sử dụng hệ thức liên quan đến vectơ để tìm tọa độ của điểm N thỏa mãn điều kiện đã cho.
Lời giải chi tiết:
a) Ta có: \(SM = \frac{2}{3}SA \Rightarrow \overrightarrow {SM} = \frac{2}{3}\overrightarrow {SA} \).
Vì \(M\) thuộc SA, nên \(MA = SA - SM\). Do đó:
\(\overrightarrow {MA} = \overrightarrow {SA} - \overrightarrow {SM} = \overrightarrow {SA} - \frac{2}{3}\overrightarrow {SA} = \frac{1}{3}\overrightarrow {SA} \).
Ta cũng có: \(\overrightarrow {AS} = - \overrightarrow {SA} \).
Suy ra: \(\overrightarrow {MA} = - \frac{1}{3}\overrightarrow {AS} \).
b) Tìm điểm \(N\) sao cho \(\overrightarrow {MN} = - \frac{2}{3}\overrightarrow {BA} \).
Ta có: \(\overrightarrow {MN} = - \frac{2}{3}\overrightarrow {BA} \to \overrightarrow {MN} = \frac{2}{3}\overrightarrow {AB} \).
Suy ra: \(MN//AB;MN = \frac{2}{3}AB\).
Tam giác SAB có đoạn thẳng MN song song với AB và \(\frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{2}{3}\) thì từ định lý Talet ta suy ra N thuộc cạnh SB:
\(\frac{{SN}}{{SB}} = \frac{2}{3} \Leftrightarrow SN = \frac{2}{3}SB\).
Trả lời câu hỏi Vận dụng 2 trang 59 SGK Toán 12 Cùng khám phá
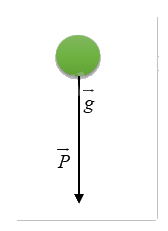
Trọng lực \(\vec P\) là lực hấp dẫn do Trái Đất tác dụng lên một vật, được tính theo công thức \(\vec P = m\vec g\), trong đó \(m\) là khối lượng của vật (đơn vị: kg), còn \(\vec g\) là vectơ gia tốc rơi tự do, có hướng đi xuống và có độ lớn \(g = 9,8{\mkern 1mu} m/{s^2}\). Xác định hướng và độ lớn của trọng lực (đơn vị: N) tác dụng lên quả bưởi có khối lượng \(2,5{\mkern 1mu} kg\).
Phương pháp giải:
- Sử dụng công thức tính trọng lực: \(\vec P = m\vec g\)
- Thay các giá trị đã cho vào công thức để tính toán.
Lời giải chi tiết:
- Khối lượng của quả bưởi: \(m = 2,5{\mkern 1mu} kg\).
- Gia tốc rơi tự do: \(g = 9,8{\mkern 1mu} m/{s^2}\).
- Trọng lực tác dụng lên quả bưởi được tính theo công thức: \(P = m \cdot g\).
- Thay các giá trị vào: \(P = 2,5 \times 9,8 = 24,5{\mkern 1mu} N\).
- Hướng của trọng lực: Hướng xuống dưới (theo chiều của vectơ \(\vec g\)).
Kết luận:
- Độ lớn của trọng lực tác dụng lên quả bưởi là \(24,5{\mkern 1mu} N\).
- Hướng của trọng lực là hướng xuống dưới.
Trả lời câu hỏi Luyện tập 5 trang 60 SGK Toán 12 Cùng khám phá
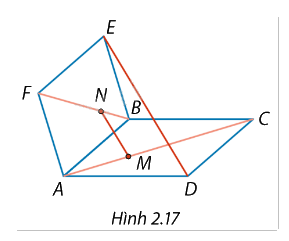
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Trên các đường chéo AC và BF lấy các điểm \(M\), \(N\) sao cho \(MC = 2MA\), \(NF = 2NB\) (Hình 2.17).
a) Biểu diễn các vectơ \(\overrightarrow {MN} \), \(\overrightarrow {DE} \) theo \(\overrightarrow {AB} \), \(\overrightarrow {AD} \), \(\overrightarrow {AF} \).
b) Từ đó suy ra MN//DE.
Phương pháp giải:
a) Áp dụng quy tắc ba điểm và quy tắc hình bình hành kết hợp với các tính chất của phép nhân một số với một vectơ.
b) Tìm k (k≠0) sao cho \(\overrightarrow {MN} = k\overrightarrow {DE} \)thì hai vectơ đó song song.
Lời giải chi tiết:
a)
Do \(MC = 2MA\), \(NF = 2NB\) nên \(\overrightarrow {AC} = - 3\overrightarrow {MA}, \overrightarrow {FB} = \frac{2}{3}\overrightarrow {FN} \).
- Biểu diễn \(\overrightarrow {MN} \)
Sử dụng quy tắc ba điểm vào \(\overrightarrow {MN} \): \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AN} = - \frac{1}{3}\overrightarrow {AC} + \overrightarrow {AF} + \frac{2}{3}\overrightarrow {FB} (*)\)
Áp dụng quy tắc hình bình hành ta có:
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(\overrightarrow {FA} + \overrightarrow {FE} = \overrightarrow {FB} \)
Thay vào (*) ta có:
\(\overrightarrow {MN} = - \frac{1}{3}(\overrightarrow {AB} + \overrightarrow {AD} ) + \overrightarrow {AF} + \frac{2}{3}(\overrightarrow {FA} + \overrightarrow {FE} ) = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {AF} + \frac{2}{3}\overrightarrow {AB} = \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {AF} \)
\(\overrightarrow {MN} = \frac{1}{3}\left( {\overrightarrow {AB} - \overrightarrow {AD} + \overrightarrow {AF} } \right)\)
- Biểu diễn \(\overrightarrow {DE} \)
Sử dụng quy tắc ba điểm vào \(\overrightarrow {DE} \):
\(\overrightarrow {DE} = \overrightarrow {DA} + \overrightarrow {AE} = - \overrightarrow {AD} + \overrightarrow {AB} + \overrightarrow {AF} \)
b) Từ câu a ta thấy \(\overrightarrow {MN} = \frac{1}{3}\overrightarrow {DE} \) suy ra MN // DE.
Mục 2 của SGK Toán 12 tập 1 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết cơ bản, các định nghĩa, định lý và công thức liên quan. Việc hiểu rõ bản chất của vấn đề sẽ giúp các em tiếp cận bài toán một cách logic và tìm ra lời giải chính xác.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về... (giả sử bài tập 1 liên quan đến giới hạn). Để giải bài tập này, ta cần:
Ví dụ: (giải chi tiết bài tập 1 với lời giải cụ thể)
Bài tập này có thể liên quan đến... (giả sử bài tập 2 liên quan đến đạo hàm). Lời giải:
Ví dụ: (giải chi tiết bài tập 2 với lời giải cụ thể)
Bài tập này thường là một bài toán ứng dụng thực tế liên quan đến... (giả sử bài tập 3 liên quan đến cực trị). Để giải quyết bài toán này, ta cần:
Ví dụ: (giải chi tiết bài tập 3 với lời giải cụ thể)
Để học toán hiệu quả, các em cần:
Khi giải bài tập Toán 12, các em cần chú ý:
Hy vọng rằng với những hướng dẫn chi tiết trên, các em sẽ tự tin giải quyết các bài tập trong mục 2 trang 58, 59, 60 SGK Toán 12 tập 1. Chúc các em học tập tốt và đạt kết quả cao!
| Bài tập | Chủ đề | Độ khó |
|---|---|---|
| Bài tập 1 | Giới hạn | Dễ |
| Bài tập 2 | Đạo hàm | Trung bình |
| Bài tập 3 | Cực trị | Khó |