Chào mừng các em học sinh đến với bài giải chi tiết bài tập 4.41 trang 38 SGK Toán 12 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
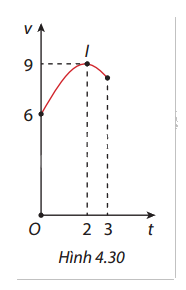
Một vật chuyển động trong 3 giờ với vận tốc \(v\) (km/h) phụ thuộc vào thời gian \(t\) (h) có đồ thị là một phần của đường parabol có đỉnh \(I(2;9)\) và trục đối xứng song song với trục tung như Hình 4.30. Tính quãng đường mà vật di chuyển được trong 3 giờ đó. A. \(25,25{\mkern 1mu} {\rm{km}}\) B. \(24,25{\mkern 1mu} {\rm{km}}\) C. \(24,75{\mkern 1mu} {\rm{km}}\) D. \(26,75{\mkern 1mu} {\rm{km}}\)
Đề bài
Một vật chuyển động trong 3 giờ với vận tốc \(v\) (km/h) phụ thuộc vào thời gian \(t\) (h) có đồ thị là một phần của đường parabol có đỉnh \(I(2;9)\) và trục đối xứng song song với trục tung như Hình 4.30. Tính quãng đường mà vật di chuyển được trong 3 giờ đó.
A. \(25,25{\mkern 1mu} {\rm{km}}\)
B. \(24,25{\mkern 1mu} {\rm{km}}\)
C. \(24,75{\mkern 1mu} {\rm{km}}\)
D. \(26,75{\mkern 1mu} {\rm{km}}\)
Phương pháp giải - Xem chi tiết
- Quãng đường mà vật di chuyển được tính bằng tích phân của vận tốc theo thời gian:
\(S = \int_0^3 v (t){\mkern 1mu} dt\)
- Hàm \(v(t)\) là một phần của parabol, có đỉnh \(I(2;9)\) và trục đối xứng song song với trục tung. Từ đó, ta cần tìm phương trình của \(v(t)\) và tính tích phân trên đoạn từ \(0\) đến \(3\).
Lời giải chi tiết
Ta biết rằng đồ thị \(v(t)\) có dạng một parabol với đỉnh \(I(2;9)\), vậy phương trình của parabol có dạng:
\(v(t) = a{(t - 2)^2} + 9\)
Dựa vào điểm \((0,6)\) trên đồ thị (vận tốc tại thời điểm \(t = 0\)), ta thay vào phương trình để tìm \(a\):
\(6 = a{(0 - 2)^2} + 9\)
\(6 = 4a + 9 \Rightarrow 4a = - 3 \Rightarrow a = - \frac{3}{4}\)
Vậy phương trình của vận tốc là:
\(v(t) = - \frac{3}{4}{(t - 2)^2} + 9\)
Bây giờ, ta tính quãng đường \(S\) bằng cách lấy tích phân:
\(S = \int_0^3 {\left( { - \frac{3}{4}{{(t - 2)}^2} + 9} \right)} dt = \int_0^3 - \frac{3}{4}{(t - 2)^2}{\mkern 1mu} dt + \int_0^3 9 {\mkern 1mu} dt\)
Tính tích phân của \(9\):
\(\int_0^3 9 {\mkern 1mu} dt = 9t|_0^3 = 9(3 - 0) = 27\)
Tính tích phân của \( - \frac{3}{4}{(t - 2)^2}\): Sử dụng biến đổi \(u = t - 2\), tích phân trở thành:
\(\int_0^3 - \frac{3}{4}{(t - 2)^2}{\mkern 1mu} dt = \int_{ - 2}^1 - \frac{3}{4}{u^2}{\mkern 1mu} du\)
Tính tích phân của \({u^2}\):
\(\int_{ - 2}^1 - \frac{3}{4}{u^2}{\mkern 1mu} du = - \frac{3}{4} \cdot \frac{{{u^3}}}{3}|_{ - 2}^1 = - \frac{1}{4}\left( {{1^3} - {{( - 2)}^3}} \right) = - \frac{1}{4}(1 + 8) = - \frac{9}{4}\)
Vậy quãng đường \(S\) là:
\(S = 27 - \frac{9}{4} = \frac{{108}}{4} - \frac{9}{4} = \frac{{99}}{4} = 24,75{\mkern 1mu} {\rm{km}}\)
Chọn C.
Bài tập 4.41 trang 38 SGK Toán 12 tập 2 là một bài toán quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về các khái niệm và định lý liên quan. Để giải bài tập này một cách hiệu quả, chúng ta cần tiếp cận theo các bước sau:
(Giả sử bài toán là về tìm đạo hàm của hàm số)
Để tìm đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1, ta sử dụng các quy tắc đạo hàm cơ bản:
Áp dụng các quy tắc này, ta có:
f'(x) = 3x2 + 4x - 5
Ngoài bài tập 4.41, còn rất nhiều bài tập tương tự trong SGK Toán 12 tập 2. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức về:
Đạo hàm là một công cụ toán học quan trọng, có nhiều ứng dụng trong thực tế, chẳng hạn như:
Để nắm vững kiến thức về đạo hàm và các ứng dụng của nó, học sinh nên luyện tập thêm các bài tập trong SGK và các tài liệu tham khảo khác. Ngoài ra, các em có thể tham gia các khóa học online hoặc tìm kiếm sự giúp đỡ của giáo viên và bạn bè.
| Hàm số f(x) | Đạo hàm f'(x) |
|---|---|
| C (hằng số) | 0 |
| xn | nxn-1 |
| sin x | cos x |
| cos x | -sin x |
| ex | ex |
Hy vọng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về bài tập 4.41 trang 38 SGK Toán 12 tập 2 và tự tin hơn trong việc học tập môn Toán.