Chào mừng các em học sinh đến với bài giải bài tập 2.8 trang 65 SGK Toán 12 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng a và (widehat {BAA'} = widehat {BAD} = widehat {DAA'} = {60^circ }). Tính độ dài đường chéo AC’.
Đề bài
Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng a và
\(\widehat {BAA'} = \widehat {BAD} = \widehat {DAA'} = {60^\circ }\). Tính độ dài đường chéo AC’.
Phương pháp giải - Xem chi tiết
Sử dụng quy tắc hình hộp và công thức tính tích vô hướng của vectơ, từ đó ta có công thức tính độ dài của \(\overrightarrow {AC'} \) là:
\(|\overrightarrow {AC'} | = \sqrt {|\overrightarrow {AB} {|^2} + |\overrightarrow {AD} {|^2} + |\overrightarrow {AA'} {|^2} + 2\overrightarrow {AB} \cdot \overrightarrow {AD} + 2\overrightarrow {AB} \cdot \overrightarrow {AA'} + 2\overrightarrow {AD} \cdot \overrightarrow {AA'} } \)
Lời giải chi tiết
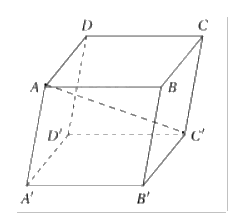
Vì tất cả các cạnh đều bằng a và các góc giữa các cặp vectơ đều là \({\rm{\backslash }}({60^\circ }{\rm{ \backslash }})\), ta có:
\(|\overrightarrow {AB} | = |\overrightarrow {AD} | = |\overrightarrow {AA'} | = a\)
Tích vô hướng giữa các cặp vectơ:
\(\overrightarrow {AB} \cdot \overrightarrow {AD} = {a^2}\cos {60^\circ } = \frac{{{a^2}}}{2}\)
\(\overrightarrow {AB} \cdot \overrightarrow {AA'} = {a^2}\cos {60^\circ } = \frac{{{a^2}}}{2}\)
\(\overrightarrow {AD} \cdot \overrightarrow {AA'} = {a^2}\cos {60^\circ } = \frac{{{a^2}}}{2}\)
Vì ABCD.A’B’C’D’ nên:
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \)
Suy ra:
\(|\overrightarrow {AC'} | = \sqrt {|\overrightarrow {AB} {|^2} + |\overrightarrow {AD} {|^2} + |\overrightarrow {AA'} {|^2} + 2\overrightarrow {AB} \cdot \overrightarrow {AD} + 2\overrightarrow {AB} \cdot \overrightarrow {AA'} + 2\overrightarrow {AD} \cdot \overrightarrow {AA'} } \)
Tính độ dài đường chéo AC':
\(|\overrightarrow {AC'} | = \sqrt {{a^2} + {a^2} + {a^2} + 2\left( {\frac{{{a^2}}}{2}} \right) + 2\left( {\frac{{{a^2}}}{2}} \right) + 2\left( {\frac{{{a^2}}}{2}} \right)} \)
\(|\overrightarrow {AC'} | = \sqrt {3{a^2} + 3{a^2}} = \sqrt {6{a^2}} = a\sqrt 6 \)
Vậy độ dài đường chéo \(AC'\) là \(a\sqrt 6 \).
Bài tập 2.8 trang 65 SGK Toán 12 tập 1 yêu cầu học sinh vận dụng kiến thức về đạo hàm để khảo sát hàm số bậc ba. Cụ thể, bài toán thường yêu cầu tìm khoảng đồng biến, nghịch biến, cực trị và vẽ đồ thị hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các bước sau:
Giả sử hàm số cần khảo sát là y = x3 - 3x2 + 2.
y' = 3x2 - 6x
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
Xét các khoảng:
y'' = 6x - 6
6x - 6 = 0 ⇔ x = 1
Xét các khoảng:
| x | -∞ | 0 | 1 | 2 | +∞ |
|---|---|---|---|---|---|
| y' | + | 0 | - | 0 | + |
| y | ↗ | max | ↘ | min | ↗ |
Dựa vào bảng biến thiên, ta có thể vẽ đồ thị hàm số y = x3 - 3x2 + 2.
Bài tập 2.8 trang 65 SGK Toán 12 tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng khảo sát hàm số bằng đạo hàm. Bằng cách nắm vững các bước giải và áp dụng linh hoạt các kiến thức đã học, các em có thể tự tin giải quyết bài toán một cách hiệu quả. Chúc các em học tập tốt!