Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Ở bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 66, 67, 68 sách giáo khoa Toán 12 tập 1.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Làm thế nào để định vị một đối tượng trong một nhà kho lớn? Bác Quản là thủ kho vật liệu của nhà máy. Trong kho có nhiều giá xếp hàng, được xếp song song với một bức tường như Hình 2.28. Nhà kho rất lớn nên để dễ dàng tìm các thùng hàng, bác dùng ba số để ghi chép vị trí của chúng theo quy ước: Số thứ nhất cho biết thùng hàng nằm ở giá nào (các giá được đánh số theo thứ tự từ trái sang phải, theo mũi tên 𝑂𝑦); Số thứ hai cho biết thùng hàng nằm ở ngăn thứ mấy của giá (các ngăn của mỗi giá đượ
Trả lời câu hỏi Hoạt động 1 trang 66 SGK Toán 12 Cùng khám phá
Làm thế nào để định vị một đối tượng trong một nhà kho lớn?
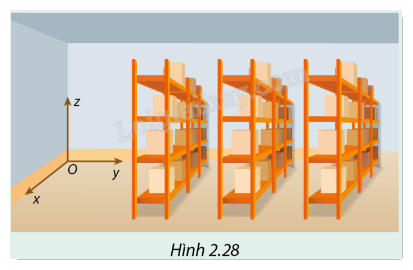
Bác Quản là thủ kho vật liệu của nhà máy. Trong kho có nhiều giá xếp hàng, được xếp song song với một bức tường như Hình 2.28.
Nhà kho rất lớn nên để dễ dàng tìm các thùng hàng, bác dùng ba số để ghi chép vị trí của chúng theo quy ước:
Số thứ nhất cho biết thùng hàng nằm ở giá nào (các giá được đánh số theo thứ tự từ trái sang phải, theo mũi tên 𝑂𝑦);
Số thứ
hai cho biết thùng hàng nằm ở ngăn thứ mấy của giá (các ngăn của mỗi giá được đánh số thứ tự từ bờ tường phía trong ra ngoài, theo mũi tên 𝑂𝑥);
Số thứ ba cho biết thùng hàng nằm ở tầng nào (các tầng của mỗi giá được đánh số thứ tự từ thấp lên cao, theo mũi tên 𝑂𝑧).
a) Hôm nay, đúng ngày bác Quản nghỉ phép thì người ta lại muốn lấy thùng đựng đinh vít cho bộ phận lắp ráp sử dụng. Biết rằng trong sổ của bác Quản có ghi: "thùng đinh vít: 5; 3; 2". Hãy chỉ dẫn cho người trực kho lấy đúng thùng đinh vít.
b) Nếu bỏ đi một trong ba số này thì việc xác định vị trí của thùng đinh vít có thuận lợi không?
Phương pháp giải:
Dựa vào hệ tọa độ được quy ước trong kho, xác định vị trí của thùng đinh vít theo ba chỉ số 𝑦, 𝑥, và 𝑧.
Sử dụng các thông tin đã cho để xác định chính xác vị trí của thùng đinh vít.
Đánh giá sự cần thiết của từng chỉ số trong việc xác định vị trí của thùng.
Lời giải chi tiết:
a) Xác định vị trí của thùng đinh vít:
Chỉ số thứ nhất (5): Thùng đinh vít nằm ở giá số 5. Ta sẽ di chuyển từ trái sang phải dọc theo trục 𝑦 đến giá số 5.
Chỉ số thứ hai (3): Thùng đinh vít nằm ở ngăn số 3 của giá. Ta sẽ di chuyển từ bức tường phía trong ra ngoài dọc theo trục 𝑥 đến ngăn thứ 3.
Chỉ số thứ ba (2): Thùng đinh vít nằm ở tầng số 2 của giá. Ta sẽ di chuyển từ tầng thấp nhất lên tầng thứ 2 dọc theo trục 𝑧.
Vì vậy, để lấy thùng đinh vít, người trực kho cần di chuyển đến giá thứ 5 (theo trục 𝑦), tìm ngăn thứ 3 (theo trục 𝑥), và cuối cùng lấy thùng từ tầng thứ 2 (theo trục 𝑧).
b) Nếu bỏ đi một trong ba số này:
Nếu bỏ số chỉ giá (thứ 1): Việc xác định giá chứa thùng đinh vít sẽ rất khó khăn vì sẽ có nhiều giá hàng khác nhau, và việc tìm kiếm sẽ mất thời gian hơn.
Nếu bỏ số chỉ ngăn (thứ 2): Điều này cũng sẽ gây khó khăn tương tự, vì sẽ có nhiều ngăn khác nhau trên cùng một giá, việc xác định ngăn chứa thùng sẽ không còn chính xác.
Nếu bỏ số chỉ tầng (thứ 3): Nếu bỏ qua chỉ số tầng, ta sẽ không biết thùng đinh vít nằm ở tầng nào, dẫn đến việc phải kiểm tra tất cả các tầng của ngăn đã xác định, làm mất thời gian và công sức.
Trả lời câu hỏi Luyện tập 1 trang 68 SGK Toán 12 Cùng khám phá
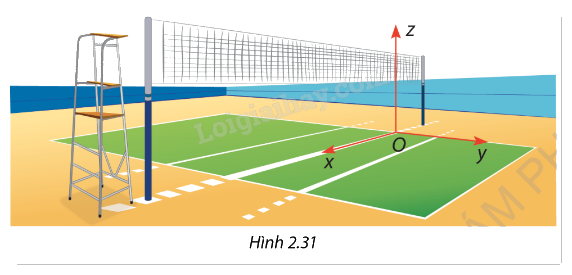
Một sân bóng chuyền với hệ tọa độ 𝑂𝑥𝑦𝑧 chọn như ở Hình 2.31. Về mặt kỹ thuật, khi dựng cột và căng lưới, người ta phải đảm bảo cho lưới nằm ở mặt phẳng tọa độ nào? Mặt phẳng đó có vuông góc với mặt sân không?
Phương pháp giải:
Dựa vào hình vẽ và mô tả, để xác định mặt phẳng chứa lưới.
Lời giải chi tiết:
Quan sát hình vẽ, ta thấy lưới bóng chuyền được căng dọc theo trục 𝑧, tức là mặt phẳng chứa lưới phải có dạng 𝑂𝑥𝑧. Như vậy, lưới nằm trên mặt phẳng 𝑂𝑥𝑧.
Mặt phẳng 𝑂𝑥𝑦 là mặt phẳng chứa mặt sân, và trục 𝑧 là trục vuông góc với mặt sân.
Mặt phẳng 𝑂𝑥𝑧 vuông góc với mặt phẳng 𝑂𝑥𝑦 tại đường thẳng giao nhau là trục 𝑂𝑥.
Trả lời câu hỏi Hoạt động 1 trang 66 SGK Toán 12 Cùng khám phá
Làm thế nào để định vị một đối tượng trong một nhà kho lớn?
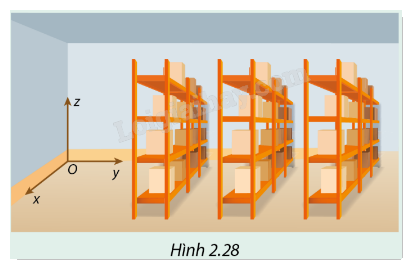
Bác Quản là thủ kho vật liệu của nhà máy. Trong kho có nhiều giá xếp hàng, được xếp song song với một bức tường như Hình 2.28.
Nhà kho rất lớn nên để dễ dàng tìm các thùng hàng, bác dùng ba số để ghi chép vị trí của chúng theo quy ước:
Số thứ nhất cho biết thùng hàng nằm ở giá nào (các giá được đánh số theo thứ tự từ trái sang phải, theo mũi tên 𝑂𝑦);
Số thứ
hai cho biết thùng hàng nằm ở ngăn thứ mấy của giá (các ngăn của mỗi giá được đánh số thứ tự từ bờ tường phía trong ra ngoài, theo mũi tên 𝑂𝑥);
Số thứ ba cho biết thùng hàng nằm ở tầng nào (các tầng của mỗi giá được đánh số thứ tự từ thấp lên cao, theo mũi tên 𝑂𝑧).
a) Hôm nay, đúng ngày bác Quản nghỉ phép thì người ta lại muốn lấy thùng đựng đinh vít cho bộ phận lắp ráp sử dụng. Biết rằng trong sổ của bác Quản có ghi: "thùng đinh vít: 5; 3; 2". Hãy chỉ dẫn cho người trực kho lấy đúng thùng đinh vít.
b) Nếu bỏ đi một trong ba số này thì việc xác định vị trí của thùng đinh vít có thuận lợi không?
Phương pháp giải:
Dựa vào hệ tọa độ được quy ước trong kho, xác định vị trí của thùng đinh vít theo ba chỉ số 𝑦, 𝑥, và 𝑧.
Sử dụng các thông tin đã cho để xác định chính xác vị trí của thùng đinh vít.
Đánh giá sự cần thiết của từng chỉ số trong việc xác định vị trí của thùng.
Lời giải chi tiết:
a) Xác định vị trí của thùng đinh vít:
Chỉ số thứ nhất (5): Thùng đinh vít nằm ở giá số 5. Ta sẽ di chuyển từ trái sang phải dọc theo trục 𝑦 đến giá số 5.
Chỉ số thứ hai (3): Thùng đinh vít nằm ở ngăn số 3 của giá. Ta sẽ di chuyển từ bức tường phía trong ra ngoài dọc theo trục 𝑥 đến ngăn thứ 3.
Chỉ số thứ ba (2): Thùng đinh vít nằm ở tầng số 2 của giá. Ta sẽ di chuyển từ tầng thấp nhất lên tầng thứ 2 dọc theo trục 𝑧.
Vì vậy, để lấy thùng đinh vít, người trực kho cần di chuyển đến giá thứ 5 (theo trục 𝑦), tìm ngăn thứ 3 (theo trục 𝑥), và cuối cùng lấy thùng từ tầng thứ 2 (theo trục 𝑧).
b) Nếu bỏ đi một trong ba số này:
Nếu bỏ số chỉ giá (thứ 1): Việc xác định giá chứa thùng đinh vít sẽ rất khó khăn vì sẽ có nhiều giá hàng khác nhau, và việc tìm kiếm sẽ mất thời gian hơn.
Nếu bỏ số chỉ ngăn (thứ 2): Điều này cũng sẽ gây khó khăn tương tự, vì sẽ có nhiều ngăn khác nhau trên cùng một giá, việc xác định ngăn chứa thùng sẽ không còn chính xác.
Nếu bỏ số chỉ tầng (thứ 3): Nếu bỏ qua chỉ số tầng, ta sẽ không biết thùng đinh vít nằm ở tầng nào, dẫn đến việc phải kiểm tra tất cả các tầng của ngăn đã xác định, làm mất thời gian và công sức.
Trả lời câu hỏi Luyện tập 1 trang 68 SGK Toán 12 Cùng khám phá
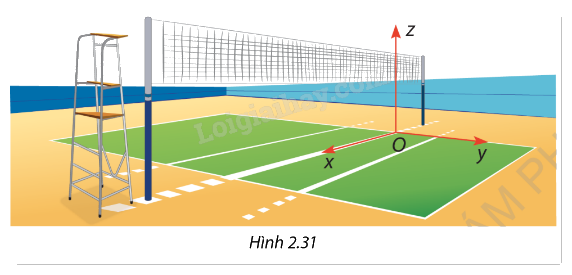
Một sân bóng chuyền với hệ tọa độ 𝑂𝑥𝑦𝑧 chọn như ở Hình 2.31. Về mặt kỹ thuật, khi dựng cột và căng lưới, người ta phải đảm bảo cho lưới nằm ở mặt phẳng tọa độ nào? Mặt phẳng đó có vuông góc với mặt sân không?
Phương pháp giải:
Dựa vào hình vẽ và mô tả, để xác định mặt phẳng chứa lưới.
Lời giải chi tiết:
Quan sát hình vẽ, ta thấy lưới bóng chuyền được căng dọc theo trục 𝑧, tức là mặt phẳng chứa lưới phải có dạng 𝑂𝑥𝑧. Như vậy, lưới nằm trên mặt phẳng 𝑂𝑥𝑧.
Mặt phẳng 𝑂𝑥𝑦 là mặt phẳng chứa mặt sân, và trục 𝑧 là trục vuông góc với mặt sân.
Mặt phẳng 𝑂𝑥𝑧 vuông góc với mặt phẳng 𝑂𝑥𝑦 tại đường thẳng giao nhau là trục 𝑂𝑥.
Mục 1 của SGK Toán 12 tập 1 thường tập trung vào các kiến thức nền tảng của một chương mới, thường là về giới hạn, đạo hàm hoặc tích phân. Việc nắm vững kiến thức này là vô cùng quan trọng để giải quyết các bài tập phức tạp hơn trong chương. Bài viết này sẽ đi sâu vào từng bài tập trong mục 1, trang 66, 67, 68, cung cấp lời giải chi tiết và các lưu ý quan trọng.
Bài tập về giới hạn thường yêu cầu học sinh vận dụng các định nghĩa và tính chất của giới hạn để tính giới hạn của một hàm số. Các dạng bài tập thường gặp bao gồm:
Ví dụ, để tính lim (x->2) (x^2 - 4) / (x - 2), ta có thể phân tích tử số thành (x - 2)(x + 2) và rút gọn với mẫu số, thu được lim (x->2) (x + 2) = 4.
Một hàm số được gọi là liên tục tại một điểm nếu giới hạn của hàm số tại điểm đó bằng giá trị của hàm số tại điểm đó. Việc xét tính liên tục của hàm số có ý nghĩa quan trọng trong việc nghiên cứu các tính chất của hàm số, như tính đơn điệu, cực trị.
Để xét tính liên tục của hàm số f(x) tại điểm x = a, ta cần kiểm tra:
Các bài tập tổng hợp thường kết hợp nhiều kiến thức và kỹ năng khác nhau về giới hạn. Để giải quyết các bài tập này, học sinh cần có khả năng phân tích bài toán, lựa chọn phương pháp phù hợp và thực hiện các phép tính chính xác.
Ví dụ, một bài tập có thể yêu cầu tính giới hạn của một hàm số phức tạp, hoặc chứng minh một biểu thức giới hạn. Trong trường hợp này, học sinh có thể cần sử dụng các định lý giới hạn, các phương pháp biến đổi đại số, hoặc các kỹ thuật tính giới hạn đặc biệt.
Ngoài SGK Toán 12 tập 1, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức về giới hạn:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 1 trang 66, 67, 68 SGK Toán 12 tập 1. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!