Chào mừng các em học sinh đến với bài giải bài tập 1.29 trang 45 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và phương pháp giải bài tập một cách hiệu quả.
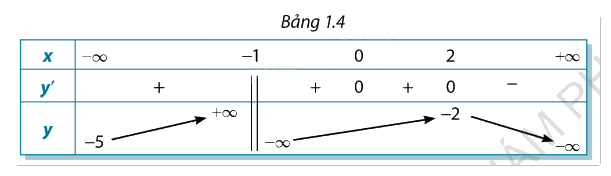
Cho hàm số \(y = f(x)\) liên tục trên các khoảng \(( - \infty ; - 1),( - 1; + \infty )\) và có bảng biến thiên như Bảng 1.4. Xác định các khoảng đồng biến, nghịch biến và cực trị của hàm số đã cho.
Đề bài
Cho hàm số \(y = f(x)\) liên tục trên các khoảng \(( - \infty ; - 1),( - 1; + \infty )\) và có bảng biến thiên như Bảng 1.4. Xác định các khoảng đồng biến, nghịch biến và cực trị của hàm số đã cho.
Phương pháp giải - Xem chi tiết
Dựa vào dấu của \(f'(x)\) trên từng khoảng để xác định chiều biến thiên và cực trị.
Lời giải chi tiết
- Hàm số \(y = f(x)\) đồng biến trên khoảng \(( - \infty ; - 1),( - 1;2)\)và nghịch biến trên khoảng \((2; + \infty )\).
- Hàm số đạt cực đại tại \(x = 2,{y_{CD}} = - 2\) và không có cực tiểu.
Bài tập 1.29 trang 45 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học môn Toán lớp 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, các em cần nắm vững các khái niệm cơ bản về đạo hàm, các quy tắc tính đạo hàm và các ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hàm số y = f(x) có đạo hàm f'(x) = (x-1)^2(x+2). Hỏi hàm số y = f(x) đồng biến trên khoảng nào?)
Để giải bài tập này, chúng ta cần xác định khoảng mà trên đó đạo hàm f'(x) dương. Vì f'(x) = (x-1)^2(x+2), ta cần xét dấu của f'(x). Lưu ý rằng (x-1)^2 luôn dương với mọi x khác 1. Do đó, dấu của f'(x) phụ thuộc vào dấu của (x+2).
Để hiểu rõ hơn về cách giải bài tập này, chúng ta hãy xem xét một ví dụ khác. (Nội dung ví dụ sẽ được chèn vào đây)
Ngoài bài tập 1.29, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 12 tập 1 để rèn luyện kỹ năng giải toán. Bên cạnh đó, các em cũng có thể tìm hiểu thêm về các ứng dụng của đạo hàm trong các lĩnh vực khác như vật lý, kinh tế, kỹ thuật,...
Bài tập 1.29 trang 45 SGK Toán 12 tập 1 là một bài toán quan trọng giúp các em củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với hướng dẫn chi tiết này, các em sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tốt!
| Quy tắc | Công thức |
|---|---|
| Đạo hàm của hằng số | (c)' = 0 |
| Đạo hàm của x^n | (x^n)' = nx^(n-1) |
| Đạo hàm của tổng | (u + v)' = u' + v' |