Giải bài tập 1.12 trang 14 SGK Toán 12 tập 1

Chào mừng các em học sinh đến với bài giải bài tập 1.12 trang 14 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về hàm số và đồ thị.

Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.

Trong các hình chữ nhật có chu vi bằng 18cm. Hãy tìm hình chữ nhật có diện tích lớn nhất

Đề bài

Trong các hình chữ nhật có chu vi bằng 18cm. Hãy tìm hình chữ nhật có diện tích lớn nhất

Phương pháp giải - Xem chi tiết Giải bài tập 1.12 trang 14 SGK Toán 12 tập 1 - Cùng khám phá 1

Bước 1: Lập công thức tính diện tích hình chữ nhật dưới dạng hàm số

Bước 2: Lập bảng biến thiên của hàm số

Bước 3: Tính diện tích lớn nhất của hình chữ nhật là tìm gía trị lớn nhất của hàm số

Lời giải chi tiết

Gọi x là chiều dài hình chữ nhật (0<x<9)

Khi đó chiều rộng hình chữ nhật là 9 - x ( > 0)

Diện tích hình chữ nhật là S(x) = x( 9 - x )

Ta có \({\rm{S'(x) = 9 - 2x}}\)

Xét \({\rm{S'(x) = 0}}\) \( \Rightarrow {\rm{x = }}\frac{{\rm{9}}}{{\rm{2}}}\)

Ta có bảng biến thiên là

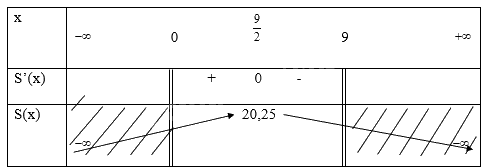
Giải bài tập 1.12 trang 14 SGK Toán 12 tập 1 - Cùng khám phá 2

Vậy diện tích lớn nhất của hình chữ nhật là 20,25 khi chiều dài và chiều rộng bằng nhau và bằng \(\frac{{\rm{9}}}{{\rm{2}}}\)

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 1.12 trang 14 SGK Toán 12 tập 1 - Cùng khám phá đặc sắc thuộc chuyên mục đề toán 12 trên nền tảng tài liệu toán. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 1.12 trang 14 SGK Toán 12 tập 1: Tổng quan

Bài tập 1.12 trang 14 SGK Toán 12 tập 1 yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, đặc biệt là các yếu tố như hệ số a, đỉnh của parabol, trục đối xứng và giao điểm với các trục tọa độ để xác định phương trình hàm số khi biết một số thông tin nhất định.

Phân tích đề bài và phương pháp giải

Để giải bài tập này một cách hiệu quả, học sinh cần:

Xác định dạng hàm số: Nhận biết đây là hàm số bậc hai có dạng y = ax² + bx + c.
Sử dụng các thông tin đã cho: Đề bài thường cung cấp các thông tin như tọa độ đỉnh, giao điểm với trục hoành, trục tung hoặc giá trị của hàm số tại một điểm cụ thể.
Lập hệ phương trình: Dựa vào các thông tin đã cho, lập hệ phương trình để tìm các hệ số a, b, c.
Giải hệ phương trình: Giải hệ phương trình để tìm ra giá trị của a, b, c.
Viết phương trình hàm số: Thay các giá trị a, b, c vừa tìm được vào dạng hàm số y = ax² + bx + c để có phương trình hàm số cần tìm.

Lời giải chi tiết bài tập 1.12 trang 14 SGK Toán 12 tập 1

(Ví dụ minh họa - cần thay thế bằng lời giải cụ thể của bài tập 1.12)

Giả sử đề bài yêu cầu tìm phương trình parabol có đỉnh I(1; -2) và đi qua điểm A(3; 2). Ta thực hiện như sau:

Dạng tổng quát của parabol: y = a(x - h)² + k, với I(h; k) là đỉnh của parabol.
Thay tọa độ đỉnh vào: y = a(x - 1)² - 2.
Thay tọa độ điểm A vào: 2 = a(3 - 1)² - 2.
Giải phương trình để tìm a: 2 = 4a - 2 => 4a = 4 => a = 1.
Phương trình parabol: y = (x - 1)² - 2 = x² - 2x - 1.

Các dạng bài tập tương tự và phương pháp giải

Ngoài bài tập 1.12, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai. Một số dạng bài tập phổ biến bao gồm:

Tìm tọa độ đỉnh của parabol: Sử dụng công thức h = -b/2a, k = -Δ/4a.
Tìm giao điểm của parabol với trục hoành và trục tung: Giải phương trình y = 0 để tìm giao điểm với trục hoành, và thay x = 0 vào phương trình để tìm giao điểm với trục tung.
Xác định khoảng đồng biến, nghịch biến của hàm số: Dựa vào dấu của hệ số a và tọa độ đỉnh.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: Dựa vào dấu của hệ số a và tọa độ đỉnh.

Mẹo giải nhanh và lưu ý quan trọng

Để giải các bài tập về hàm số bậc hai một cách nhanh chóng và chính xác, học sinh nên:

Nắm vững các công thức: Công thức tính tọa độ đỉnh, trục đối xứng, giao điểm với các trục tọa độ.
Sử dụng máy tính bỏ túi: Để tính toán nhanh chóng và chính xác.
Vẽ đồ thị hàm số: Để hình dung rõ hơn về tính chất của hàm số.
Kiểm tra lại kết quả: Để đảm bảo tính chính xác.

Bài tập luyện tập

Để củng cố kiến thức, các em có thể tự giải các bài tập sau:

Bài 1: Tìm phương trình parabol có đỉnh I(-2; 3) và đi qua điểm B(0; -1).
Bài 2: Tìm tọa độ đỉnh và trục đối xứng của hàm số y = 2x² - 4x + 1.
Bài 3: Tìm giao điểm của parabol y = x² - 3x + 2 với trục hoành.

Kết luận

Bài tập 1.12 trang 14 SGK Toán 12 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tốt!