Chào mừng các em học sinh đến với bài giải bài tập 3.10 trang 104 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
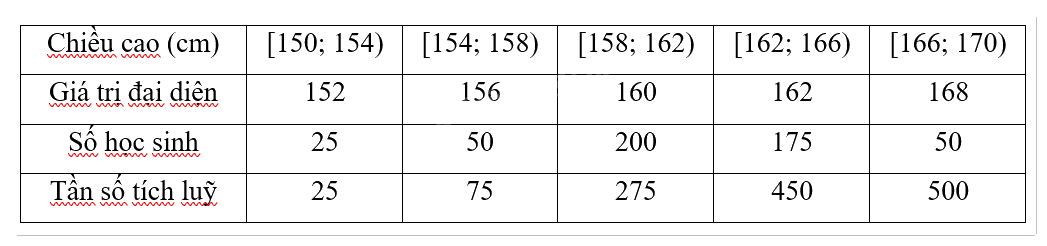
Chiều cao của 500 học sinh một trường trung học cơ sở được thống kê trong Bảng 3.25.
Đề bài
Chiều cao của 500 học sinh một trường trung học cơ sở được thống kê trong Bảng 3.25.

a) Tính khoảng tứ phân vị, trung bình và độ lệch chuẩn chiều cao của 500 học sinh.
b) Kết quả tìm được cho biết điều gì về chiều cao của 500 học sinh này?
Phương pháp giải - Xem chi tiết
a)
- Công thức tìm tứ phân vị: \({Q_x} = L + \left( {\frac{{{n_x} - F}}{f}} \right) \times h\)
- Khoảng tứ phân vị là khoảng giữa \({Q_3}\) và \({Q_1}\), ký hiệu là:\({\Delta _Q} = {Q_3} - {Q_1}\)
- Công thức tính trung bình là:
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{n_i}} \right)} }}{N}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {\overline {{x^2}} - {{\left( {\overline x } \right)}^2}} = \sqrt {\frac{{\sum {{f_i}x_i^2} }}{N} - {{\left( {\overline x } \right)}^2}} \)
b)
Trung bình: Cho biết giá trị trung bình chiều cao của 500 học sinh. Nếu trung bình cao, có thể suy ra rằng chiều cao của nhóm này nói chung là cao.
Độ lệch chuẩn: Cho biết mức độ phân tán của các chiều cao xung quanh giá trị trung bình. Nếu độ lệch chuẩn lớn, điều đó có nghĩa là chiều cao của các học sinh rất khác nhau. Ngược lại, độ lệch chuẩn nhỏ cho thấy chiều cao của học sinh khá đồng đều.
Khoảng tứ phân vị: Giúp xác định sự phân tán của phần lớn dữ liệu (tức là 50% giữa). Nếu khoảng tứ phân vị nhỏ, điều đó cho thấy rằng phần lớn học sinh có chiều cao gần nhau. Nếu khoảng tứ phân vị lớn, điều đó chỉ ra rằng có sự khác biệt lớn về chiều cao giữa các học sinh.
Lời giải chi tiết
a)
Tứ phân vị:
- \(\frac{N}{4} = 125\) rơi vào nhóm [158; 162)
\({Q_1} = 158 + \frac{{125 - 75}}{{200}}.4 = 159\)
- \(\frac{{3N}}{4} = 375\) rơi vào nhóm [162; 166)
\({Q_3} = 162 + \frac{{375 - 275}}{{175}}.4 = 164,29\)
Khoảng tứ phân vị:
\({\Delta _Q} = {Q_3} - {Q_1} = 164,29 - 159 \approx 5,29\)
Chiều cao trung bình:
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{n_i}} \right)} }}{N} = \frac{{152.25 + 156.50 + 160.200 + 164.175 + 168.50}}{{500}} = 161,4\)
Độ lệch chuẩn chiều cao của 500 học sinh:
- Tính \(\overline {{x^2}} \):
\(\overline {x_G^2} = \frac{{\sum {{f_i}.x_i^2} }}{N} = \frac{{{{152}^2}.25 + {{156}^2}.50 + {{160}^2}.200 + {{164}^2}.175 + {{168}^2}.50}}{{500}} = 26064,8\)
- Tính độ lệch chuẩn
\(S = \sqrt {\overline {{x^2}} - {{\left( {\overline x } \right)}^2}} = \sqrt {26064,8 - 161,{4^2}} \approx 3,85\)cm
b) Nhận xét về chiều cao của 500 học sinh:
Trung bình chiều cao là 161.4 cm, cho thấy chiều cao trung bình của nhóm học sinh này rơi vào khoảng giữa của dãy chiều cao đã cho.
Độ lệch chuẩn là 3.85 cm, điều này cho thấy có sự phân tán tương đối nhỏ về chiều cao giữa các học sinh. Phần lớn học sinh có chiều cao gần với giá trị trung bình.
Như vậy, các giá trị tứ phân vị cho thấy rằng 25% học sinh có chiều cao dưới 159 cm và 75% học sinh có chiều cao dưới 164.29 cm, với sự phân tán khoảng 5.29 cm giữa \({Q_1}\) và \({Q_3}\).
Bài tập 3.10 trang 104 SGK Toán 12 tập 1 thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để tìm cực trị của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Giả sử hàm số cần khảo sát là: y = x3 - 3x2 + 2
Hàm số y = x3 - 3x2 + 2 có tập xác định là D = R (tập hợp tất cả các số thực).
y' = 3x2 - 6x
Giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2 là các điểm dừng của hàm số.
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Dựa vào bảng biến thiên, ta có thể kết luận:
Ngoài bài tập 3.10, SGK Toán 12 tập 1 còn nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết. Các dạng bài tập này thường bao gồm:
Để giải quyết các bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bảng biến thiên và các phương pháp giải toán liên quan.
Khi giải bài tập về đạo hàm, học sinh cần lưu ý một số điểm sau:
Hy vọng với bài giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài tập 3.10 trang 104 SGK Toán 12 tập 1 và các bài tập tương tự. Chúc các em học tập tốt!