Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong SGK Toán 12 tập 2. Mục 1 của chương trình Toán 12 tập 2 tập trung vào các kiến thức quan trọng về đạo hàm, ứng dụng của đạo hàm trong việc khảo sát hàm số.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập phức tạp. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bộ giải chi tiết, giúp bạn hiểu rõ bản chất của từng bài toán.
Trong Hình 4.10, gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số (y = x - 3), trục hoành và các đường thẳng (x = 1) và (x = 6).
Trả lời câu hỏi Luyện tập 1 trang 23 SGK Toán 12 Cùng khám phá
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành và các đường thẳng \(x = - 3,x = 2\).
Phương pháp giải:
- Xác định ình phẳng cần tính diện tích.
- Phân tích dấu của hàm \(y = {x^3}\).
- Tìm biểu thức diện tích tổng quát.
- Tính các tích phân dựa trên biểu thức diện tích tổng quát.
Lời giải chi tiết:
Hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành \(y = 0\), và hai đường thẳng \(x = - 3\) và \(x = 2\). Tại các khoảng khác nhau, đồ thị có thể nằm bên trên hoặc bên dưới trục hoành, nên cần tính tích phân của giá trị tuyệt đối \(|{x^3}|\) để đảm bảo kết quả diện tích là dương.
- Từ \(x = - 3\) đến \(x = 0\), \(y = {x^3}\) là âm.
- Từ \(x = 0\) đến \(x = 2\), \(y = {x^3}\) là dương.
Diện tích hình phẳng được tính bằng cách lấy tích phân của \(|{x^3}|\) từ \(x = - 3\) đến \(x = 2\)
\(S = \int_{ - 3}^0 - {x^3}{\mkern 1mu} dx + \int_0^2 {{x^3}} {\mkern 1mu} dx\)
Trong khoảng \(x \in [ - 3,0]\), đổi dấu hàm số \({x^3}\) để đảm bảo diện tích là dương.
Tích phân của \( - {x^3}\) trong khoảng \([ - 3,0]\):
\(\int_{ - 3}^0 - {x^3}{\mkern 1mu} dx = - \left[ {\frac{{{x^4}}}{4}} \right]_{ - 3}^0 = - \left( {\frac{{{0^4}}}{4} - \frac{{{{( - 3)}^4}}}{4}} \right) = - \left( {0 - \frac{{81}}{4}} \right) = \frac{{81}}{4}\)
Tích phân của \({x^3}\) trong khoảng \(\left[ {0,{\rm{ }}2} \right]\):
\(\int_0^2 {{x^3}} {\mkern 1mu} dx = \left[ {\frac{{{x^4}}}{4}} \right]_0^2 = \frac{{{2^4}}}{4} - \frac{{{0^4}}}{4} = \frac{{16}}{4} = 4\)
Diện tích tổng cộng là tổng của hai kết quả tích phân:
\(S = \frac{{81}}{4} + 4 = \frac{{81}}{4} + \frac{{16}}{4} = \frac{{97}}{4}\)
Vậy, diện tích của hình phẳng là:
\(S = \frac{{97}}{4} = 24.25\).
Trả lời câu hỏi Hoạt động 1 trang 22 SGK Toán 12 Cùng khám phá
Trong Hình 4.10, gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y = x - 3\), trục hoành và các đường thẳng \(x = 1\) và \(x = 6\).
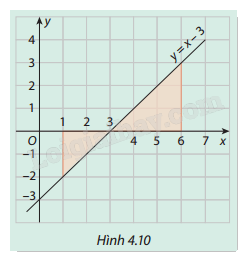
a) Tính diện tích của (H).
b) Tính các tích phân \(\int_1^6 {(x - 3)} {\mkern 1mu} dx\) và \(\int_1^6 | x - 3|{\mkern 1mu} dx\). So sánh hai tích phân này với kết quả tính được ở câu a và rút ra nhận xét.
Phương pháp giải:
a)
Diện tích (H) có thể tính bằng cách cộng diện tích của hai tam giác. Diện tích của tam giác được tính bằng công thức:
\(S = \frac{1}{2} \times h \times \)đáy
b)
- Tính trực tiếp các tích phân \(\int_1^6 {(x - 3)dx} \) và \(\int_1^6 {\left| {x - 3} \right|dx} \).
- So sánh kết quả của hai tích phân này với diện tích tính được ở câu a để rút ra nhận xét.
Lời giải chi tiết:
a)
Hình phẳng (H) trong đề bài là hai hình tam giác vuông, với các cạnh là:
- Đáy của tam giác thứ nhất: \(6 - 3 = 3\)
- Chiều cao của tam giác thứ nhất: \(3 - 0 = 3\)
- Đáy của tam giác thứ hai: \(3 - 1 = 2\)
- Chiều cao của tam giác thứ nhất: \(0 - ( - 2) = 2\)
Diện tích tam giác được tính theo công thức:
\(S = \frac{1}{2} \times 3 \times 3 + \frac{1}{2} \times 2 \times 2 = \frac{9}{2} + 2 = 6,5\)
b)
Tính tích phân thứ nhất:
\(\int_1^6 {(x - 3)} {\mkern 1mu} dx = \left[ {\frac{{{{(x - 3)}^2}}}{2}} \right]_1^6 = \frac{9}{2} - 2 = \frac{7}{2} = 2,5\)
Tính tích phân thứ hai:
\(\int_1^6 | x - 3|{\mkern 1mu} dx = \int_1^3 {(3 - x)} {\mkern 1mu} dx + \int_3^6 {(x - 3)} {\mkern 1mu} dx = 2 + \frac{9}{2} = 6,5\)
Nhận xét:
- Tích phân thứ nhất \(\int_1^6 {(x - 3)} {\mkern 1mu} dx = 3.5\) không phản ánh diện tích thực của hình phẳng, vì hàm số nhận giá trị âm trong khoảng từ 1 đến 3.
- Tích phân thứ hai \(\int_1^6 | x - 3|{\mkern 1mu} dx = 6.5\) chính là diện tích hình phẳng tính được ở câu a, vì nó tính giá trị tuyệt đối của hàm số, tức là cả phần âm và phần dương.
Trả lời câu hỏi Luyện tập 2 trang 26 SGK Toán 12 Cùng khám phá
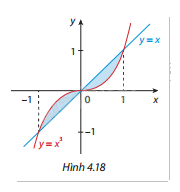
Tính diện tích hình phẳng được tô màu trong Hình 4.18.
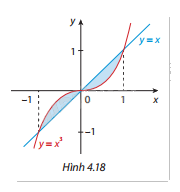
Phương pháp giải:
- Xác định giao điểm của hai đường \(y = {x^3}\) và \(y = x\) bằng cách giải phương trình: \({x^3} = x\)
- Diện tích hình phẳng giữa hai đường cong \(y = {x^3}\) và \(y = x\) trong khoảng từ \(x = - 1\) đến \(x = 1\) được tính bằng:
\(S = \int_{ - 1}^1 | x - {x^3}|{\mkern 1mu} dx\)
Lời giải chi tiết:
Giao điểm của hai đường \(y = {x^3}\) và \(y = x\) là:
\({x^3} = x \Leftrightarrow x({x^2} - 1) = 0\)
Suy ra: \(x = 0\), \(x = 1\), và \(x = - 1\).
Vì trên khoảng từ \( - 1\) đến 0, \(y = {x^3}\) nằm trên \(y = x\), và trên khoảng từ 0 đến 1, \(y = x\) nằm trên \(y = {x^3}\), ta có:
\(S = \int_{ - 1}^0 {({x^3} - x)} {\mkern 1mu} dx + \int_0^1 {(x - {x^3})} {\mkern 1mu} dx\)
Tính tích phân:
\(\int_{ - 1}^0 {({x^3} - x)} {\mkern 1mu} dx = \left[ {\frac{{{x^4}}}{4} - \frac{{{x^2}}}{2}} \right]_{ - 1}^0 = \left( {0 - 0} \right) - \left( {\frac{1}{4} - \frac{1}{2}} \right) = - \frac{1}{4} + \frac{1}{2} = \frac{1}{4}\)
\(\int_0^1 {(x - {x^3})} {\mkern 1mu} dx = \left[ {\frac{{{x^2}}}{2} - \frac{{{x^4}}}{4}} \right]_0^1 = \left( {\frac{1}{2} - \frac{1}{4}} \right) - (0 - 0) = \frac{1}{4}\)
Vậy diện tích hình phẳng là:
\(S = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\).
Trả lời câu hỏi Hoạt động 2 trang 24 SGK Toán 12 Cùng khám phá
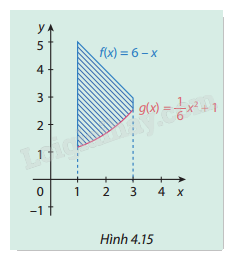
Cho hai hàm số \(f(x) = 6 - x\), \(g(x) = \frac{1}{6}{x^2} + 1\).
a) Tính \({S_1}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1,{\rm{ }}x = 3\) và đồ thị hàm số \(y = f\left( x \right).\)
b) Tính \({S_2}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1,{\rm{ }}x = 3\) và đồ thị hàm số \(y = g\left( x \right).\)
c) Qua \({S_1},\,\,{S_2}\) tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số
\(y = f\left( x \right),{\rm{ }}y = g\left( x \right)\) và các đường thẳng \(x = 1,{\rm{ }}x = 3\). (phần hình phẳng được gạch chéo trong Hình 4.15).
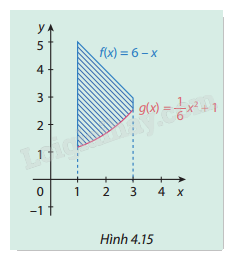
Phương pháp giải:
a) Tính diện tích \({S_1}\) bằng cách lấy tích phân của hàm số \(f(x) = 6 - x\) từ \(x = 1\) đến \(x = 3\)
b) Tính diện tích \({S_2}\) bằng cách lấy tích phân của hàm số \(g(x) = \frac{1}{6}{x^2} + 1\) từ \(x = 1\) đến \(x = 3\).
c) Tính diện tích hình phẳng giới hạn bởi hai đồ thị bằng cách lấy hiệu diện tích \({S_1} - {S_2}\).
Lời giải chi tiết:
a) Tính \({S_1}\)
Diện tích \({S_1}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1\), \(x = 3\) và đồ thị hàm số \(y = f(x)\):
\({S_1} = \int_1^3 {(6 - x)} dx\)
Tính tích phân:
\({S_1} = \left[ {6x - \frac{{{x^2}}}{2}} \right]_1^3\)
\({S_1} = \left( {6 \cdot 3 - \frac{{{3^2}}}{2}} \right) - \left( {6 \cdot 1 - \frac{{{1^2}}}{2}} \right)\)
\({S_1} = (18 - 4.5) - (6 - 0.5) = 13.5 - 5.5 = 8\)
b) Tính \({S_2}\)
Diện tích \({S_2}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1\), \(x = 3\) và đồ thị hàm số \(y = g(x)\):
\({S_2} = \int_1^3 {\left( {\frac{1}{6}{x^2} + 1} \right)} dx\)
Tính tích phân:
\({S_2} = \left[ {\frac{1}{6} \cdot \frac{{{x^3}}}{3} + x} \right]_1^3\)
\({S_2} = \left( {\frac{1}{6} \cdot \frac{{27}}{3} + 3} \right) - \left( {\frac{1}{6} \cdot \frac{1}{3} + 1} \right)\)
\({S_2} = \left( {\frac{9}{6} + 3} \right) - \left( {\frac{1}{{18}} + 1} \right)\)
\({S_2} = (1.5 + 3) - \left( {\frac{1}{{18}} + 1} \right) = 4.5 - \frac{{19}}{{18}} = \frac{{81}}{{18}} - \frac{{19}}{{18}} = \frac{{62}}{{18}} \approx 3,44\)
c) Tính diện tích hình phẳng giữa hai đồ thị
Diện tích hình phẳng giới hạn bởi hai đồ thị \(f(x)\) và \(g(x)\) trong khoảng \(x = 1\) đến \(x = 3\) là:
\(S = {S_1} - {S_2} = 8 - 3,44 = 4,56\)
Vậy, diện tích hình phẳng giữa hai đồ thị là \(S = 4,56\).
Trả lời câu hỏi Vận dụng 1 trang 24 SGK Toán 12 Cùng khám phá
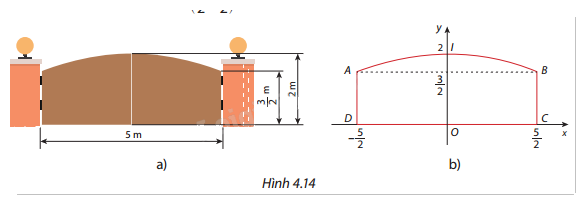
Một cái cổng có kích thước như Hình 4.14a. Vòm cổng có hình dạng một parabol có đỉnh \(I(0;2)\) và đi qua điểm \(B\left( {\frac{5}{2};\frac{3}{2}} \right)\) như Hình 4.14b. Tính diện tích hai cánh cửa cổng.
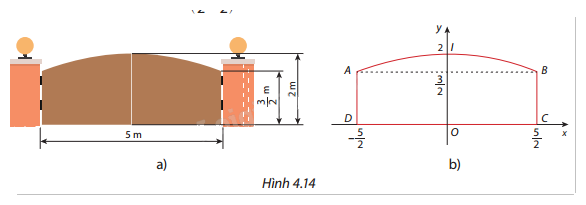
Phương pháp giải:
- Xác định phương trình parabol.
- Tính diện tích một cánh cửa cổng bằng cách tính tích phân diện tích hình phẳng giới hạn bởi parabol và trục hoành trong khoảng từ \(x = 0\) đến \(x = \frac{5}{2}\).
- Nhân diện tích một cánh cửa với 2 để ra diện tích hai cánh cửa cổng.
Lời giải chi tiết:
Xác định phương trình parabol đỉnh \(I(0;2)\) có dạng:
\(y = a{x^2} + 2\)
Sử dụng điểm \(B\left( {\frac{5}{2};\frac{3}{2}} \right)\) để tìm hệ số \(a\):
\(\frac{3}{2} = a{\left( {\frac{5}{2}} \right)^2} + 2\)
Giải ra ta được:
\(a = - \frac{2}{{25}}\)
Vậy phương trình của parabol là:
\(y = - \frac{2}{{25}}{x^2} + 2\)
Diện tích một cánh cửa là diện tích hình phẳng giới hạn bởi parabol và trục hoành trong khoảng từ \(x = 0\) đến \(x = \frac{5}{2}\), được tính bằng tích phân:
\(S = 2\int_0^{\frac{5}{2}} {\left( { - \frac{2}{{25}}{x^2} + 2} \right)} dx\)
Tính tích phân:
\(S = 2\left[ {\left( { - \frac{2}{{25}} \cdot \frac{{{x^3}}}{3} + 2x} \right)} \right]_0^{\frac{5}{2}}\)
\(S = 2\left[ { - \frac{2}{{25}} \cdot \frac{{125}}{{24}} + 2 \cdot \frac{5}{2}} \right]\)
\(S = 2\left( { - \frac{5}{{12}} + 5} \right) = 2\left( {\frac{{55}}{{12}}} \right) = \frac{{55}}{6}\)
Vậy, diện tích hai cánh cửa cổng là: \(9,167{{\rm{m}}^2}\).
Trả lời câu hỏi Hoạt động 1 trang 22 SGK Toán 12 Cùng khám phá
Trong Hình 4.10, gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y = x - 3\), trục hoành và các đường thẳng \(x = 1\) và \(x = 6\).
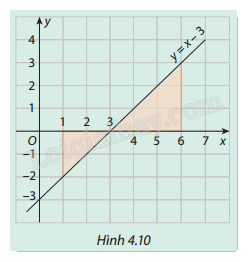
a) Tính diện tích của (H).
b) Tính các tích phân \(\int_1^6 {(x - 3)} {\mkern 1mu} dx\) và \(\int_1^6 | x - 3|{\mkern 1mu} dx\). So sánh hai tích phân này với kết quả tính được ở câu a và rút ra nhận xét.
Phương pháp giải:
a)
Diện tích (H) có thể tính bằng cách cộng diện tích của hai tam giác. Diện tích của tam giác được tính bằng công thức:
\(S = \frac{1}{2} \times h \times \)đáy
b)
- Tính trực tiếp các tích phân \(\int_1^6 {(x - 3)dx} \) và \(\int_1^6 {\left| {x - 3} \right|dx} \).
- So sánh kết quả của hai tích phân này với diện tích tính được ở câu a để rút ra nhận xét.
Lời giải chi tiết:
a)
Hình phẳng (H) trong đề bài là hai hình tam giác vuông, với các cạnh là:
- Đáy của tam giác thứ nhất: \(6 - 3 = 3\)
- Chiều cao của tam giác thứ nhất: \(3 - 0 = 3\)
- Đáy của tam giác thứ hai: \(3 - 1 = 2\)
- Chiều cao của tam giác thứ nhất: \(0 - ( - 2) = 2\)
Diện tích tam giác được tính theo công thức:
\(S = \frac{1}{2} \times 3 \times 3 + \frac{1}{2} \times 2 \times 2 = \frac{9}{2} + 2 = 6,5\)
b)
Tính tích phân thứ nhất:
\(\int_1^6 {(x - 3)} {\mkern 1mu} dx = \left[ {\frac{{{{(x - 3)}^2}}}{2}} \right]_1^6 = \frac{9}{2} - 2 = \frac{7}{2} = 2,5\)
Tính tích phân thứ hai:
\(\int_1^6 | x - 3|{\mkern 1mu} dx = \int_1^3 {(3 - x)} {\mkern 1mu} dx + \int_3^6 {(x - 3)} {\mkern 1mu} dx = 2 + \frac{9}{2} = 6,5\)
Nhận xét:
- Tích phân thứ nhất \(\int_1^6 {(x - 3)} {\mkern 1mu} dx = 3.5\) không phản ánh diện tích thực của hình phẳng, vì hàm số nhận giá trị âm trong khoảng từ 1 đến 3.
- Tích phân thứ hai \(\int_1^6 | x - 3|{\mkern 1mu} dx = 6.5\) chính là diện tích hình phẳng tính được ở câu a, vì nó tính giá trị tuyệt đối của hàm số, tức là cả phần âm và phần dương.
Trả lời câu hỏi Luyện tập 1 trang 23 SGK Toán 12 Cùng khám phá
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành và các đường thẳng \(x = - 3,x = 2\).
Phương pháp giải:
- Xác định ình phẳng cần tính diện tích.
- Phân tích dấu của hàm \(y = {x^3}\).
- Tìm biểu thức diện tích tổng quát.
- Tính các tích phân dựa trên biểu thức diện tích tổng quát.
Lời giải chi tiết:
Hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành \(y = 0\), và hai đường thẳng \(x = - 3\) và \(x = 2\). Tại các khoảng khác nhau, đồ thị có thể nằm bên trên hoặc bên dưới trục hoành, nên cần tính tích phân của giá trị tuyệt đối \(|{x^3}|\) để đảm bảo kết quả diện tích là dương.
- Từ \(x = - 3\) đến \(x = 0\), \(y = {x^3}\) là âm.
- Từ \(x = 0\) đến \(x = 2\), \(y = {x^3}\) là dương.
Diện tích hình phẳng được tính bằng cách lấy tích phân của \(|{x^3}|\) từ \(x = - 3\) đến \(x = 2\)
\(S = \int_{ - 3}^0 - {x^3}{\mkern 1mu} dx + \int_0^2 {{x^3}} {\mkern 1mu} dx\)
Trong khoảng \(x \in [ - 3,0]\), đổi dấu hàm số \({x^3}\) để đảm bảo diện tích là dương.
Tích phân của \( - {x^3}\) trong khoảng \([ - 3,0]\):
\(\int_{ - 3}^0 - {x^3}{\mkern 1mu} dx = - \left[ {\frac{{{x^4}}}{4}} \right]_{ - 3}^0 = - \left( {\frac{{{0^4}}}{4} - \frac{{{{( - 3)}^4}}}{4}} \right) = - \left( {0 - \frac{{81}}{4}} \right) = \frac{{81}}{4}\)
Tích phân của \({x^3}\) trong khoảng \(\left[ {0,{\rm{ }}2} \right]\):
\(\int_0^2 {{x^3}} {\mkern 1mu} dx = \left[ {\frac{{{x^4}}}{4}} \right]_0^2 = \frac{{{2^4}}}{4} - \frac{{{0^4}}}{4} = \frac{{16}}{4} = 4\)
Diện tích tổng cộng là tổng của hai kết quả tích phân:
\(S = \frac{{81}}{4} + 4 = \frac{{81}}{4} + \frac{{16}}{4} = \frac{{97}}{4}\)
Vậy, diện tích của hình phẳng là:
\(S = \frac{{97}}{4} = 24.25\).
Trả lời câu hỏi Vận dụng 1 trang 24 SGK Toán 12 Cùng khám phá
Một cái cổng có kích thước như Hình 4.14a. Vòm cổng có hình dạng một parabol có đỉnh \(I(0;2)\) và đi qua điểm \(B\left( {\frac{5}{2};\frac{3}{2}} \right)\) như Hình 4.14b. Tính diện tích hai cánh cửa cổng.
Phương pháp giải:
- Xác định phương trình parabol.
- Tính diện tích một cánh cửa cổng bằng cách tính tích phân diện tích hình phẳng giới hạn bởi parabol và trục hoành trong khoảng từ \(x = 0\) đến \(x = \frac{5}{2}\).
- Nhân diện tích một cánh cửa với 2 để ra diện tích hai cánh cửa cổng.
Lời giải chi tiết:
Xác định phương trình parabol đỉnh \(I(0;2)\) có dạng:
\(y = a{x^2} + 2\)
Sử dụng điểm \(B\left( {\frac{5}{2};\frac{3}{2}} \right)\) để tìm hệ số \(a\):
\(\frac{3}{2} = a{\left( {\frac{5}{2}} \right)^2} + 2\)
Giải ra ta được:
\(a = - \frac{2}{{25}}\)
Vậy phương trình của parabol là:
\(y = - \frac{2}{{25}}{x^2} + 2\)
Diện tích một cánh cửa là diện tích hình phẳng giới hạn bởi parabol và trục hoành trong khoảng từ \(x = 0\) đến \(x = \frac{5}{2}\), được tính bằng tích phân:
\(S = 2\int_0^{\frac{5}{2}} {\left( { - \frac{2}{{25}}{x^2} + 2} \right)} dx\)
Tính tích phân:
\(S = 2\left[ {\left( { - \frac{2}{{25}} \cdot \frac{{{x^3}}}{3} + 2x} \right)} \right]_0^{\frac{5}{2}}\)
\(S = 2\left[ { - \frac{2}{{25}} \cdot \frac{{125}}{{24}} + 2 \cdot \frac{5}{2}} \right]\)
\(S = 2\left( { - \frac{5}{{12}} + 5} \right) = 2\left( {\frac{{55}}{{12}}} \right) = \frac{{55}}{6}\)
Vậy, diện tích hai cánh cửa cổng là: \(9,167{{\rm{m}}^2}\).
Trả lời câu hỏi Hoạt động 2 trang 24 SGK Toán 12 Cùng khám phá
Cho hai hàm số \(f(x) = 6 - x\), \(g(x) = \frac{1}{6}{x^2} + 1\).
a) Tính \({S_1}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1,{\rm{ }}x = 3\) và đồ thị hàm số \(y = f\left( x \right).\)
b) Tính \({S_2}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1,{\rm{ }}x = 3\) và đồ thị hàm số \(y = g\left( x \right).\)
c) Qua \({S_1},\,\,{S_2}\) tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số
\(y = f\left( x \right),{\rm{ }}y = g\left( x \right)\) và các đường thẳng \(x = 1,{\rm{ }}x = 3\). (phần hình phẳng được gạch chéo trong Hình 4.15).
Phương pháp giải:
a) Tính diện tích \({S_1}\) bằng cách lấy tích phân của hàm số \(f(x) = 6 - x\) từ \(x = 1\) đến \(x = 3\)
b) Tính diện tích \({S_2}\) bằng cách lấy tích phân của hàm số \(g(x) = \frac{1}{6}{x^2} + 1\) từ \(x = 1\) đến \(x = 3\).
c) Tính diện tích hình phẳng giới hạn bởi hai đồ thị bằng cách lấy hiệu diện tích \({S_1} - {S_2}\).
Lời giải chi tiết:
a) Tính \({S_1}\)
Diện tích \({S_1}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1\), \(x = 3\) và đồ thị hàm số \(y = f(x)\):
\({S_1} = \int_1^3 {(6 - x)} dx\)
Tính tích phân:
\({S_1} = \left[ {6x - \frac{{{x^2}}}{2}} \right]_1^3\)
\({S_1} = \left( {6 \cdot 3 - \frac{{{3^2}}}{2}} \right) - \left( {6 \cdot 1 - \frac{{{1^2}}}{2}} \right)\)
\({S_1} = (18 - 4.5) - (6 - 0.5) = 13.5 - 5.5 = 8\)
b) Tính \({S_2}\)
Diện tích \({S_2}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1\), \(x = 3\) và đồ thị hàm số \(y = g(x)\):
\({S_2} = \int_1^3 {\left( {\frac{1}{6}{x^2} + 1} \right)} dx\)
Tính tích phân:
\({S_2} = \left[ {\frac{1}{6} \cdot \frac{{{x^3}}}{3} + x} \right]_1^3\)
\({S_2} = \left( {\frac{1}{6} \cdot \frac{{27}}{3} + 3} \right) - \left( {\frac{1}{6} \cdot \frac{1}{3} + 1} \right)\)
\({S_2} = \left( {\frac{9}{6} + 3} \right) - \left( {\frac{1}{{18}} + 1} \right)\)
\({S_2} = (1.5 + 3) - \left( {\frac{1}{{18}} + 1} \right) = 4.5 - \frac{{19}}{{18}} = \frac{{81}}{{18}} - \frac{{19}}{{18}} = \frac{{62}}{{18}} \approx 3,44\)
c) Tính diện tích hình phẳng giữa hai đồ thị
Diện tích hình phẳng giới hạn bởi hai đồ thị \(f(x)\) và \(g(x)\) trong khoảng \(x = 1\) đến \(x = 3\) là:
\(S = {S_1} - {S_2} = 8 - 3,44 = 4,56\)
Vậy, diện tích hình phẳng giữa hai đồ thị là \(S = 4,56\).
Trả lời câu hỏi Luyện tập 2 trang 26 SGK Toán 12 Cùng khám phá
Tính diện tích hình phẳng được tô màu trong Hình 4.18.
Phương pháp giải:
- Xác định giao điểm của hai đường \(y = {x^3}\) và \(y = x\) bằng cách giải phương trình: \({x^3} = x\)
- Diện tích hình phẳng giữa hai đường cong \(y = {x^3}\) và \(y = x\) trong khoảng từ \(x = - 1\) đến \(x = 1\) được tính bằng:
\(S = \int_{ - 1}^1 | x - {x^3}|{\mkern 1mu} dx\)
Lời giải chi tiết:
Giao điểm của hai đường \(y = {x^3}\) và \(y = x\) là:
\({x^3} = x \Leftrightarrow x({x^2} - 1) = 0\)
Suy ra: \(x = 0\), \(x = 1\), và \(x = - 1\).
Vì trên khoảng từ \( - 1\) đến 0, \(y = {x^3}\) nằm trên \(y = x\), và trên khoảng từ 0 đến 1, \(y = x\) nằm trên \(y = {x^3}\), ta có:
\(S = \int_{ - 1}^0 {({x^3} - x)} {\mkern 1mu} dx + \int_0^1 {(x - {x^3})} {\mkern 1mu} dx\)
Tính tích phân:
\(\int_{ - 1}^0 {({x^3} - x)} {\mkern 1mu} dx = \left[ {\frac{{{x^4}}}{4} - \frac{{{x^2}}}{2}} \right]_{ - 1}^0 = \left( {0 - 0} \right) - \left( {\frac{1}{4} - \frac{1}{2}} \right) = - \frac{1}{4} + \frac{1}{2} = \frac{1}{4}\)
\(\int_0^1 {(x - {x^3})} {\mkern 1mu} dx = \left[ {\frac{{{x^2}}}{2} - \frac{{{x^4}}}{4}} \right]_0^1 = \left( {\frac{1}{2} - \frac{1}{4}} \right) - (0 - 0) = \frac{1}{4}\)
Vậy diện tích hình phẳng là:
\(S = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\).
Mục 1 của SGK Toán 12 tập 2 là nền tảng quan trọng để học sinh nắm vững kiến thức về đạo hàm và ứng dụng của nó. Nội dung chính bao gồm các khái niệm cơ bản về đạo hàm, các quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc khảo sát hàm số. Việc hiểu rõ các khái niệm này là điều kiện tiên quyết để giải quyết các bài toán phức tạp hơn trong chương trình học.
Các bài tập trên trang 22 tập trung vào việc kiểm tra sự hiểu biết của học sinh về khái niệm đạo hàm, ý nghĩa hình học và vật lý của đạo hàm. Học sinh cần nắm vững định nghĩa đạo hàm và biết cách tính đạo hàm của một số hàm số đơn giản.
Trang 23 giới thiệu các quy tắc tính đạo hàm như quy tắc cộng, trừ, nhân, chia, quy tắc hàm hợp. Học sinh cần luyện tập thành thạo các quy tắc này để có thể tính đạo hàm của các hàm số phức tạp hơn.
Các trang 24, 25 và 26 tập trung vào việc ứng dụng đạo hàm để khảo sát hàm số, bao gồm tìm khoảng đồng biến, nghịch biến, cực trị, điểm uốn và vẽ đồ thị hàm số. Đây là phần quan trọng nhất của mục 1, đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm và kỹ năng phân tích hàm số.
| Bài tập | Nội dung |
|---|---|
| Bài 7 | Tìm khoảng đồng biến, nghịch biến của hàm số y = x3 - 3x2 + 2. |
| Bài 8 | Tìm cực đại, cực tiểu của hàm số y = x4 - 4x2 + 3. |
| Bài 9 | Tìm điểm uốn của hàm số y = x5 - 5x3. |
Để giải các bài tập trong mục 1 một cách hiệu quả, học sinh cần:
Đừng ngần ngại tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè nếu bạn gặp khó khăn trong quá trình học tập. Hãy dành thời gian ôn tập và làm thêm các bài tập để củng cố kiến thức. Sử dụng các công cụ hỗ trợ học tập trực tuyến như giaitoan.edu.vn để có thêm nguồn tài liệu và lời giải chi tiết.
Giải mục 1 trang 22, 23, 24, 25, 26 SGK Toán 12 tập 2 là bước quan trọng để học sinh làm chủ kiến thức về đạo hàm và ứng dụng của nó. Với sự hướng dẫn chi tiết và phương pháp giải bài tập hiệu quả, giaitoan.edu.vn hy vọng sẽ giúp bạn học tập tốt hơn và đạt kết quả cao trong môn Toán.