Chào mừng bạn đến với bài học về lý thuyết các quy tắc tính xác suất trong chương trình Toán 12. Đây là một phần kiến thức quan trọng, thường xuyên xuất hiện trong các đề thi THPT Quốc gia và các kỳ thi đại học. Bài học này sẽ cung cấp cho bạn một cái nhìn tổng quan và chi tiết về các quy tắc cơ bản, giúp bạn tự tin giải quyết các bài toán liên quan.
Giaitoan.edu.vn cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu, cùng với hệ thống bài tập đa dạng để bạn có thể luyện tập và củng cố kiến thức một cách hiệu quả.
1. Công thức xác suất toàn phần
1. Công thức xác suất toàn phần
Cho hai biến cố A và B với 0 < P(B) < 1. Khi đó \(P(A) = P(B).P(A|B) + P(\overline B ).P(A|\overline B )\) gọi là công thức xác suất toàn phần. |
Ví dụ 1: Người ta khảo sát khả năng chơi nhạc cụ của một nhóm học sinh tại trường X. Nhóm này có 60% học sinh là nam. Kết quả khảo sát cho thấy 20% học sinh nam và 15% học sinh nữ biết chơi ít nhất một nhạc cụ. Chọn ngẫu nhiên một sinh trong nhóm này. Tính xác suất để chọn được học sinh biết chơi ít nhất một nhạc cụ.
Giải:
Xét phép thử chọn ngẫu nhiên một học sinh trong nhóm.
Gọi A là biến cố "Chọn được một học sinh biết chơi ít nhất một nhạc cụ" và B, \(\overline B \) lần lượt là các biến cố "Chọn được học sinh nam" và "Chọn được một học sinh nữ".
Theo đề bài: \(P\left( B \right) = 60\% = 0,6\); \(P\left( {\overline B } \right) = 1 - 0,6 = 0,4\);
\(P(A\mid B) = 20\% = 0,2\); \(P(A\mid \overline B ) = 15\% = 0,15.\)
Áp dụng công thức xác suất toàn phần, ta có:
\(P\left( A \right) = P\left( B \right) \cdot P(A\mid B) + P\left( {\overline B } \right) \cdot P(A\mid \overline B ) = 0,6 \cdot 0,2 + 0,4 \cdot 0,15 = 0,18.\)
Vậy xác suất để chọn được một học sinh biết chơi nhạc cụ là 0,18 hay 18%.
Ví dụ 2: Có hai hộp đựng các viên bi cùng kích thước và khối lượng. Hộp thứ nhất chứa 5 viên bi đỏ và 5 viên bi xanh, hộp thứ hai chứa 6 viên bi đỏ và 4 viên bi xanh. Lấy ngẫu nhiên một viên bi từ hộp thứ nhất chuyển sang hộp thứ hai, sau đó lấy ra ngẫu nhiên một viên bi từ hộp thứ hai. Tính xác suất để viên bi được lấy ra từ hộp thứ hai là viên bi đỏ.
Giải:
Cách 1:
Gọi:
A là biến cố "Viên bi được lấy ra từ hộp thứ hai là bi đỏ";
B là biến cố "Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi đỏ";
\(\overline B \) là biến cố "Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh".
Ta có: \(P\left( B \right) = \frac{5}{{10}} = \frac{1}{2}\); \(P\left( {\overline B } \right) = \frac{5}{{10}} = \frac{1}{2}\).
Nếu viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi đỏ thì sau khi chuyển, hộp thứ hai có 7 bi đỏ và 4 bi xanh. Do đó \(P(A\mid B) = \frac{7}{{11}}\).
Nếu viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh thì sau khi chuyển, hộp thứ hai có 6 bi đỏ và 5 bi xanh. Do đó \(P(A\mid \overline B ) = \frac{6}{{11}}\).
Áp dụng công thức xác suất toàn phần, ta có:
\(P\left( A \right) = P\left( B \right) \cdot P(A\mid B) + P\left( {\overline B } \right) \cdot P(A\mid \overline B ) = \frac{1}{2} \cdot \frac{7}{{11}} + \frac{1}{2} \cdot \frac{6}{{11}} = \frac{{13}}{{22}}\).
Vậy xác suất để viên bi được lấy ra từ hộp thứ hai là bi đỏ bằng \(\frac{{13}}{{22}}\).
Cách 2:
Gọi:
A là biến cố "Viên bi được lấy ra từ hộp thứ hai là bi đỏ";
C là biến cố "Viên bi được lấy ra từ hộp thứ hai là bi của hộp thứ nhất";
\(\overline C \) là biến cố "Viên bi được lấy ra từ hộp thứ hai là bi của hộp thứ hai".
Sau khi chuyển một viên bi từ hộp thứ nhất sang hộp thứ hai thì hộp thứ hai có 11 viên bi.
Ta có: \(P\left( C \right) = \frac{1}{{11}}\); \(P\left( {\overline C } \right) = \frac{{10}}{{11}}\).
Xác suất để viên bi được lấy ra từ hộp thứ hai là bi đỏ của hộp thứ nhất: \(P(A\mid C) = \frac{5}{{10}} = \frac{1}{2}\).
Xác suất để viên bi được lấy ra từ hộp thứ hai là bi đỏ của hộp thứ hai: \(P(A\mid \overline C ) = \frac{6}{{10}} = \frac{3}{5}\).
Áp dụng công thức xác suất toàn phần, ta có:
\(P\left( A \right) = P\left( C \right) \cdot P(A\mid C) + P\left( {\overline C } \right) \cdot P(A\mid \overline C ) = \frac{1}{{11}} \cdot \frac{1}{2} + \frac{{10}}{{11}} \cdot \frac{3}{5} = \frac{{13}}{{22}}\).
Vậy xác suất để viên bi được lấy ra từ hộp thứ hai là bi đỏ bằng \(\frac{{13}}{{22}}\).
2. Công thức Bayes
Với hai biến cố A, B mà P(A) > 0: \(P(B|A) = \frac{{P(B).P(A|B)}}{{P(A)}}\) |
Lưu ý: Do \(P(A) = P(B).P(A|B) + P(\overline B ).P(A|\overline B )\) nên công thức Bayes còn có dạng \(P(B|A) = \frac{{P(B).P(A|B)}}{{P(B).P(A|B) + P(\overline B ).P(A|\overline B )}}\).
Ví dụ 1: Cho hai biến cố A, B sao cho P(A) = 0,6; P(B) = 0,4; P(A|B) = 0,3. Tính P(B|A).
Giải:
Áp dụng công thức Bayes, ta có: \(P(B|A) = \frac{{P(B).P(A|B)}}{{P(A)}} = \frac{{0,4.0,3}}{{0,6}} = 0,2\).
Ví dụ 2: Kết quả khảo sát tại một xã cho thấy có 20% cư dân hút thuốc lá. Tỉ lệ cư dân thường xuyên gặp các vấn đề sức khỏe về đường hô hấp trong số những người hút thuốc lá và không hút thuốc lá lần lượt là 70%, 15%.
a) Nếu ta gặp một cư dân của xã thì xác suất người đó thường xuyên gặp các vấn đề sức khỏe về đường hô hấp là bao nhiêu?
b) Nếu ta gặp một cư dân của xã thường xuyên gặp các vấn đề sức khỏe về đường hô hấp thì xác suất người đó có hút thuốc lá là bao nhiêu?
Giải:
Giả sử ta gặp một cư dân của xã, gọi A là biến cố "Người đó có hút thuốc lá" và B là biến cố "Người đó thường xuyên gặp các vấn đề sức khỏe về đường hô hấp". Ta có sơ đồ hình cây sau:
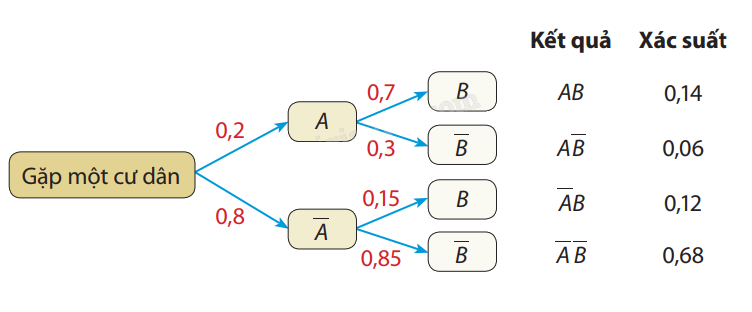
a) Ta có: \(P\left( B \right) = P\left( A \right).P(B\mid A) + P\left( {\overline A } \right).P(B\mid \overline A ) = 0,14 + 0,12 = 0,26.\)
Vậy nếu ta gặp một cư dân của xã thì xác suất người đó thường xuyên gặp các vấn đề sức khỏe về đường hô hấp là 26%.
b) Theo công thức Bayes, ta có: \(P(A\mid B) = \frac{{P\left( A \right)P(B\mid A)}}{{P\left( B \right)}} = \frac{{0,14}}{{0,26}} \approx 0,54.\) Vậy nếu ta gặp một cư dân của xã thường xuyên gặp các vấn đề sức khỏe về đường hô hấp thì xác suất người đó có hút thuốc lá là khoảng 54%.

Xác suất là một khái niệm quan trọng trong toán học, đặc biệt là trong chương trình Toán 12. Nó giúp chúng ta đánh giá khả năng xảy ra của một sự kiện nào đó. Để hiểu rõ hơn về xác suất, chúng ta cần nắm vững các quy tắc tính xác suất cơ bản.
Xác suất của một sự kiện A, ký hiệu là P(A), là một số thực nằm trong khoảng [0, 1]. P(A) cho biết khả năng xảy ra của sự kiện A. Nếu P(A) = 0, sự kiện A không thể xảy ra. Nếu P(A) = 1, sự kiện A chắc chắn xảy ra.
Ví dụ 1: Tung một con xúc xắc 6 mặt. Tính xác suất để tung được mặt 5.
Giải: Không gian mẫu của thí nghiệm là S = {1, 2, 3, 4, 5, 6}. Biến cố A là tung được mặt 5, A = {5}. Số phần tử của không gian mẫu là |S| = 6. Số phần tử của biến cố A là |A| = 1. Vậy, P(A) = |A| / |S| = 1/6.
Ví dụ 2: Rút một lá bài từ bộ bài 52 lá. Tính xác suất để rút được lá Át.
Giải: Không gian mẫu của thí nghiệm là S (tất cả 52 lá bài). Biến cố A là rút được lá Át, có 4 lá Át trong bộ bài. Vậy, P(A) = 4/52 = 1/13.
Để nắm vững lý thuyết các quy tắc tính xác suất, bạn cần luyện tập thường xuyên với các bài tập khác nhau. Hãy tìm kiếm các bài tập trên internet, trong sách giáo khoa hoặc các trang web học toán online như giaitoan.edu.vn. Đừng ngại hỏi thầy cô hoặc bạn bè nếu bạn gặp khó khăn.
Ngoài các quy tắc cơ bản, còn có nhiều khái niệm và công thức liên quan đến xác suất, như phân phối xác suất, biến ngẫu nhiên, kỳ vọng toán học, phương sai, độ lệch chuẩn,... Bạn có thể tìm hiểu thêm về các khái niệm này để nâng cao kiến thức về xác suất.
Xác suất có rất nhiều ứng dụng trong thực tế, như trong thống kê, kinh tế, tài chính, bảo hiểm, y học, khoa học tự nhiên,... Ví dụ, trong thống kê, xác suất được sử dụng để phân tích dữ liệu và đưa ra các kết luận về một tổng thể. Trong tài chính, xác suất được sử dụng để đánh giá rủi ro và lợi nhuận của các khoản đầu tư.
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết các quy tắc tính xác suất Toán 12. Chúc bạn học tập tốt và đạt kết quả cao trong kỳ thi!