Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 1 trang 59 sách bài tập Toán 8 Chân trời sáng tạo tập 2. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và phù hợp với trình độ của học sinh. Hãy cùng theo dõi bài viết để có được kết quả tốt nhất trong học tập!
Cho tam giác ABC, hãy vẽ tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số đồng dạng \(k = \frac{3}{5}\).
Đề bài
Cho tam giác ABC, hãy vẽ tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số đồng dạng \(k = \frac{3}{5}\).
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về định nghĩa hai tam giác đồng dạng để vẽ hình: Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu \(\widehat {A'} = \widehat A,\widehat {B'} = \widehat B,\widehat {C'} = \widehat C,\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\) (k gọi là tỉ số đồng dạng)
+ Sử dụng kiến thức về định lí về hai tam giác đồng dạng: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết
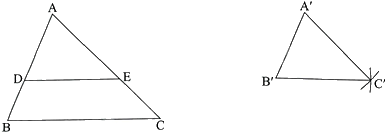
Trên cạnh AB lấy điểm D sao cho \(AD = \frac{3}{5}AB\).
Từ D kẻ đường thẳng song song với BC và cắt AC tại E.
Khi đó, tam giác ADE đồng dạng với tam giác ABC theo tỉ số đồng dạng \(k = \frac{3}{5}\)
Dựng \(\Delta A'B'C' = \Delta ADE\):
+ Dựng \(A'B' = AD\).
+ Dựng cung tròn tâm A’ bán kính AE và cung tròn tâm B’ bán kính DE, hai cung tròn này cắt nhau tại C’.
+ Nối B’C’, A’C’ ta được tam giác A’B’C’ phải dựng.
Ta có $\Delta ADE\backsim \Delta ABC$ theo tỉ số đồng dạng \(k = \frac{3}{5}\) nên tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số đồng dạng \(k = \frac{3}{5}\).
Bài 1 trang 59 sách bài tập Toán 8 Chân trời sáng tạo tập 2 thuộc chương trình học về các phép biến đổi đơn giản với đa thức. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài tập này thường yêu cầu học sinh thực hiện các phép toán đơn giản với đa thức, hoặc phân tích đa thức thành nhân tử để tìm ra nghiệm.
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết như sau:
Ví dụ:
Câu a yêu cầu thu gọn biểu thức: 3x2 + 2x - 5x2 + x + 1
Giải:
3x2 + 2x - 5x2 + x + 1 = (3x2 - 5x2) + (2x + x) + 1 = -2x2 + 3x + 1
Ví dụ:
Câu b yêu cầu tìm nghiệm của đa thức: x2 - 4 = 0
Giải:
x2 - 4 = 0 ⇔ x2 = 4 ⇔ x = ±2
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự sau:
Khi giải bài tập về đa thức, các em cần lưu ý những điều sau:
Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài 1 trang 59 sách bài tập Toán 8 Chân trời sáng tạo tập 2. Chúc các em học tập tốt!