Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 sách Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 2 trang 40, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
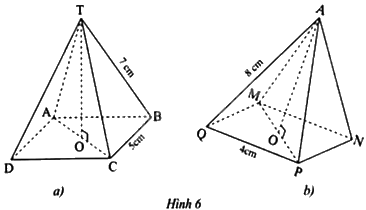
Hãy cho biết tên các mặt bên, mặt đáy, đường cao và độ dài cạnh bên, cạnh đáy của mỗi hình chóp tứ giác đều ở Hình 6.
Đề bài
Hãy cho biết tên các mặt bên, mặt đáy, đường cao và độ dài cạnh bên, cạnh đáy của mỗi hình chóp tứ giác đều ở Hình 6.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về hình chóp tứ giác đều để tìm mặt bên, mặt đáy, đường cao và độ dài cạnh bên, cạnh đáy của mỗi hình chóp tứ giác đều:
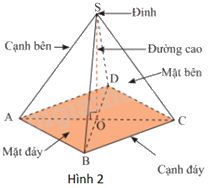Hình S.ABCD (Hình 2) là một hình chóp tứ giác đều. Trong hình này:
+ Mặt ABCD là một hình vuông và được gọi là mặt đáy (gọi tắt là đáy).
+ Các đoạn thẳng SA, SB, SC, SD bằng nhau và được gọi là các cạnh bên.
+ Ba mặt SAB, SDC, SBC, SAD là các tam giác cân đỉnh S bằng nhau và được gọi là bốn mặt bên.
+ Các đoạn thẳng AB, BC, CD, DA được gọi là cạnh đáy.
+ Gọi O là giao điểm của hai đường chéo của mặt đáy, khi đó SO gọi là đường cao, độ dài SO là chiều cao.
Lời giải chi tiết
* Hình a:
- Mặt bên: TAB, TCD, TBC, TDA
- Mặt đáy: ABCD
- Đường cao: TO
- Độ dài cạnh bên: 7cm
- Độ dài cạnh đáy: 5cm
* Hình b:
- Mặt bên: AMN, ANP, APQ, AQM
- Mặt đáy: MNPQ
- Đường cao: AO
- Độ dài cạnh bên: 8cm
- Độ dài cạnh đáy: 4cm
Bài 2 trang 40 sách bài tập Toán 8 Chân trời sáng tạo thuộc chương trình học về các phép biến đổi đơn giản với đa thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về thu gọn đa thức, tìm bậc của đa thức và các phép toán cộng, trừ đa thức để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương trình toán học nâng cao hơn.
Bài 2 trang 40 thường bao gồm các dạng bài tập sau:
Để giúp bạn giải bài 2 trang 40 một cách hiệu quả, chúng tôi sẽ cung cấp hướng dẫn chi tiết cho từng phần của bài tập. Dưới đây là một ví dụ minh họa:
Đề bài: Thu gọn đa thức sau: A = 3x2y + 2xy2 - 5x2y + 4xy2
Lời giải:
Áp dụng các bước trên, ta có:
A = (3x2y - 5x2y) + (2xy2 + 4xy2)
A = -2x2y + 6xy2
Vậy, đa thức A sau khi thu gọn là: -2x2y + 6xy2
Để giải các bài tập về đa thức một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo sau:
Việc học tốt các kiến thức về đa thức là rất quan trọng vì nó là nền tảng cho nhiều chương trình toán học nâng cao hơn, như giải phương trình, giải bất phương trình, và các bài toán về hàm số. Nếu bạn nắm vững kiến thức về đa thức, bạn sẽ có lợi thế lớn trong việc học tập các môn học khác liên quan đến toán học.
Hy vọng rằng với hướng dẫn chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong việc giải bài 2 trang 40 sách bài tập Toán 8 Chân trời sáng tạo. Hãy luyện tập thường xuyên để củng cố kiến thức và đạt kết quả tốt nhất trong học tập. Chúc bạn thành công!
