Giải bài 4 trang 52 Sách bài tập Toán 8 - Chân trời sáng tạo

Giải bài 4 trang 52 sách bài tập toán 8 - Chân trời sáng tạo

Giải bài 4 trang 52 Sách bài tập Toán 8 - Chân trời sáng tạo

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 sách Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 4 trang 52, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.

Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán.

Tính độ dài x trong Hình 6

Đề bài

Tính độ dài x trong Hình 6

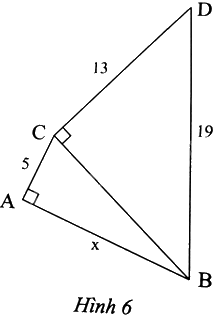
Giải bài 4 trang 52 sách bài tập toán 8 - Chân trời sáng tạo 1

Phương pháp giải - Xem chi tiết Giải bài 4 trang 52 sách bài tập toán 8 - Chân trời sáng tạo 2

Sử dụng kiến thức về định lí Pythagore vào tam giác vuông để tìm x: Trong một tam giác vuông, bình vuông độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.

Lời giải chi tiết

Áp dụng định lí Pythagore vào tam giác DBC vuông tại C có:

\(C{D^2} + B{C^2} = D{B^2}\), suy ra \(B{C^2} = D{B^2} - C{D^2} = {19^2} - {13^2} = 192\)

Áp dụng định lí Pythagore vào tam giác ABC vuông tại A có:

\(A{C^2} + A{B^2} = C{B^2}\), suy ra \(A{B^2} = C{B^2} - A{C^2} = 192 - {5^2} = 167\), do đó \(x = \sqrt {167} cm\)

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 4 trang 52 sách bài tập toán 8 - Chân trời sáng tạo đặc sắc thuộc chuyên mục giải sách giáo khoa toán 8 trên đề thi toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 4 trang 52 Sách bài tập Toán 8 - Chân trời sáng tạo: Tổng quan

Bài 4 trang 52 sách bài tập Toán 8 Chân trời sáng tạo thuộc chương trình học về các tứ giác đặc biệt, cụ thể là hình thang cân. Bài tập này thường yêu cầu học sinh vận dụng các tính chất của hình thang cân để giải quyết các vấn đề liên quan đến độ dài cạnh, góc, đường chéo và diện tích.

Nội dung bài tập

Bài 4 thường bao gồm các dạng bài tập sau:

Chứng minh một tứ giác là hình thang cân: Yêu cầu học sinh sử dụng các dấu hiệu nhận biết hình thang cân (hai cạnh đáy song song và hai cạnh bên bằng nhau, hoặc hai góc kề một cạnh bên bằng nhau).
Tính độ dài các cạnh, góc của hình thang cân: Dựa vào các tính chất của hình thang cân (hai cạnh bên bằng nhau, hai góc kề một cạnh bên bằng nhau, hai đường chéo bằng nhau) để tính toán.
Tính diện tích hình thang cân: Sử dụng công thức diện tích hình thang: S = (a + b)h/2, trong đó a và b là độ dài hai đáy, h là chiều cao.
Bài toán thực tế liên quan đến hình thang cân: Áp dụng kiến thức về hình thang cân để giải quyết các bài toán thực tế.

Hướng dẫn giải chi tiết bài 4 trang 52

Để giải bài 4 trang 52 sách bài tập Toán 8 Chân trời sáng tạo một cách hiệu quả, bạn cần:

Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán, các dữ kiện đã cho và những điều cần tìm.
Vẽ hình: Vẽ hình minh họa bài toán, chú thích các điểm và đường thẳng quan trọng.
Phân tích bài toán: Xác định các mối quan hệ giữa các yếu tố trong bài toán, lựa chọn phương pháp giải phù hợp.
Thực hiện giải bài: Áp dụng các kiến thức và công thức đã học để giải bài toán, trình bày lời giải một cách rõ ràng, logic.
Kiểm tra lại kết quả: Đảm bảo kết quả của bạn là chính xác và phù hợp với điều kiện của bài toán.

Ví dụ minh họa

Bài toán: Cho hình thang cân ABCD (AB // CD), AB = 6cm, CD = 10cm, AD = BC = 5cm. Tính chiều cao của hình thang.

Giải:

Kẻ AH và BK vuông góc với CD (H, K thuộc CD). Khi đó, AH = BK là chiều cao của hình thang.

Vì ABCD là hình thang cân nên DH = KC = (CD - AB)/2 = (10 - 6)/2 = 2cm.

Xét tam giác vuông ADH, ta có: AH² = AD² - DH² = 5² - 2² = 21.

Vậy, AH = √21 cm. Do đó, chiều cao của hình thang là √21 cm.

Các lưu ý khi giải bài tập về hình thang cân

Nắm vững các tính chất của hình thang cân.
Sử dụng các dấu hiệu nhận biết hình thang cân một cách linh hoạt.
Chú ý đến việc vẽ hình và phân tích bài toán một cách cẩn thận.
Kiểm tra lại kết quả sau khi giải bài.

Tài liệu tham khảo

Ngoài sách giáo khoa và sách bài tập, bạn có thể tham khảo thêm các tài liệu sau:

Các trang web học toán online uy tín.
Các video hướng dẫn giải bài tập Toán 8 trên YouTube.
Các diễn đàn trao đổi kiến thức Toán học.

Kết luận

Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 4 trang 52 sách bài tập Toán 8 Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!