Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 8. Bài viết này sẽ hướng dẫn bạn cách giải bài 6 trang 10 sách bài tập toán 8 - Chân trời sáng tạo tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Tìm tọa độ của các điểm A, B, C, D, E và F trong Hình 10.
Đề bài
Tìm tọa độ của các điểm A, B, C, D, E và F trong Hình 10.
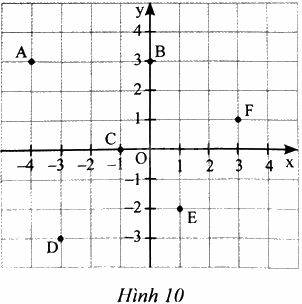
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức tọa độ của một điểm trong mặt phẳng tọa độ: Ta xác định vị trí của điểm P trong mặt phẳng tọa độ Oxy bằng cách sau: Từ P vẽ các đường vuông góc với các trục tọa độ cắt trục hoành tại điểm a và trục tung tại điểm b. Khi đó cặp số (a; b) gọi là tọa độ của điểm P và kí hiệu P (a; b). Số a gọi là hoành độ và số b gọi là tung độ của điểm P.
Lời giải chi tiết
\(A\left( { - 4;3} \right),{\rm{ }}B\left( {0;3} \right),{\rm{ }}C\left( { - 1;0} \right),{\rm{ }}D\left( { - 3; - 3} \right),{\rm{ }}E\left( {1; - 2} \right),F\left( {3;1} \right)\)
Bài 6 trang 10 sách bài tập toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các định lý liên quan.
Bài tập 6 yêu cầu học sinh chứng minh một số tính chất liên quan đến đường trung bình của tam giác và hình thang. Để giải bài tập này, học sinh cần:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ cung cấp hướng dẫn giải chi tiết cho từng câu hỏi:
Để chứng minh câu a, ta cần sử dụng định nghĩa đường trung bình của tam giác và các tính chất của hình bình hành. Cụ thể, ta có thể thực hiện các bước sau:
Để chứng minh câu b, ta cần sử dụng định nghĩa đường trung bình của hình thang và các tính chất của hình bình hành. Cụ thể, ta có thể thực hiện các bước sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ cung cấp một ví dụ minh họa:
Ví dụ: Cho tam giác ABC, M là trung điểm của AB và N là trung điểm của AC. Chứng minh MN song song với BC và MN = BC/2.
Giải:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể tự giải các bài tập tương tự trong sách bài tập toán 8 - Chân trời sáng tạo tập 2. Ngoài ra, học sinh cũng có thể tham khảo các tài liệu học tập khác trên internet hoặc tại các thư viện.
Bài 6 trang 10 sách bài tập toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh nắm vững kiến thức về đường trung bình của tam giác và hình thang. Hy vọng rằng, với hướng dẫn giải chi tiết và ví dụ minh họa trên, học sinh có thể tự tin giải bài tập này một cách hiệu quả.
| Công thức/Định lý | Nội dung |
|---|---|
| Đường trung bình của tam giác | Đường trung bình của tam giác là đoạn thẳng nối trung điểm của hai cạnh của tam giác. Đường trung bình song song với cạnh thứ ba và bằng một nửa cạnh thứ ba. |
| Đường trung bình của hình thang | Đường trung bình của hình thang là đoạn thẳng nối trung điểm của hai cạnh bên của hình thang. Đường trung bình song song với hai đáy và bằng trung bình cộng của hai đáy. |