Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 8 trang 64 sách bài tập Toán 8 - Chân trời sáng tạo tập 2. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 8 trang 64 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Cho tam giác đều ABC, từ B và C kẻ các đường thẳng song song với AC và AB, hai đường thẳng này cắt nhau tại M.
Đề bài
Cho tam giác đều ABC, từ B và C kẻ các đường thẳng song song với AC và AB, hai đường thẳng này cắt nhau tại M. Qua M kẻ đường thẳng cắt AB tại E và cắt AC tại F. Chứng minh rằng:
a) \(\frac{{CA}}{{CF}} = \frac{{ME}}{{MF}}\) và \(\frac{{BE}}{{BA}} = \frac{{ME}}{{MF}}\).
b) $\Delta BCE\backsim \Delta CFB$.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về trường hợp đồng dạng thứ hai của hai tam giác (c.g.c) để tính chứng minh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
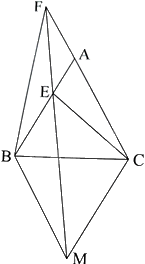
a) Tam giác FCM có AE//CM nên theo định lí Thalès ta có: \(\frac{{CA}}{{CF}} = \frac{{ME}}{{MF}}\)
Tam giác FAE có AF//BM nên theo hệ quả định lí Thalès ta có: \(\frac{{AE}}{{BE}} = \frac{{EF}}{{ME}}\)
Ta có: \(\frac{{AE}}{{BE}} + \frac{{BE}}{{BE}} = \frac{{EF}}{{ME}} + \frac{{ME}}{{ME}}\), suy ra \(\frac{{BA}}{{BE}} = \frac{{MF}}{{ME}}\) hay \(\frac{{BE}}{{BA}} = \frac{{ME}}{{MF}}\)
b) Ta có: \(\frac{{CA}}{{CF}} = \frac{{BE}}{{BA}}\left( { = \frac{{ME}}{{MF}}} \right)\), mà \(AB = AC = BC\)
Do đó, \(\frac{{BC}}{{CF}} = \frac{{BE}}{{CB}}\), lại có: \(\widehat {EBC} = \widehat {BCF}\) (do tam giác ABC đều) nên $\Delta BCE\backsim \Delta CFB\left( c.g.c \right)$
Bài 8 trang 64 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Bài tập yêu cầu học sinh chứng minh các tính chất, tính toán độ dài đoạn thẳng, góc và diện tích liên quan đến hình thang cân. Việc nắm vững kiến thức nền tảng và kỹ năng giải toán là yếu tố then chốt để hoàn thành bài tập này một cách hiệu quả.
Bài 8 trang 64 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thường bao gồm các dạng bài tập sau:
Để giải bài tập bài 8 trang 64 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Bài tập: Cho hình thang cân ABCD (AB // CD), AB = 5cm, CD = 10cm, AD = 6cm. Tính độ dài đường cao của hình thang.
Lời giải:
Kẻ AH và BK vuông góc với CD (H, K thuộc CD). Ta có: DH = KC = (CD - AB) / 2 = (10 - 5) / 2 = 2.5cm.
Xét tam giác vuông ADH, ta có: AH2 = AD2 - DH2 = 62 - 2.52 = 36 - 6.25 = 29.75.
Vậy, AH = √29.75 ≈ 5.45cm. Do đó, đường cao của hình thang là 5.45cm.
Để củng cố kiến thức và kỹ năng giải bài tập về hình thang cân, bạn có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 8 - Chân trời sáng tạo tập 2 và các nguồn tài liệu khác. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và tự tin hơn trong các bài kiểm tra.
Bài 8 trang 64 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hình thang cân và các tính chất của nó. Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, bạn sẽ tự tin hơn trong việc giải toán và đạt kết quả tốt trong học tập.