Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 48 sách bài tập Toán 8 - Chân trời sáng tạo tập 2. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 8.
Chúng tôi sẽ cung cấp đáp án, phương pháp giải bài tập một cách rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong các bài kiểm tra.
Cho hình bình hành ABCD có tia phân giác của góc A cắt đường chéo BD tại M và tia phân giác của góc D cắt đường chéo AC tại N. Chứng minh MN//AD.
Đề bài
Cho hình bình hành ABCD có tia phân giác của góc A cắt đường chéo BD tại M và tia phân giác của góc D cắt đường chéo AC tại N. Chứng minh MN//AD.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất của đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.
Lời giải chi tiết
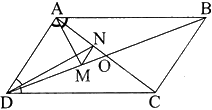
Gọi O là giao điểm của AC và BD nên \(AC = 2AO,BD = 2DO\)
Vì DN là phân giác của góc ADC trong tam giác ADC nên: \(\frac{{NA}}{{NC}} = \frac{{AD}}{{DC}}\)
Vì AM là phân giác của góc DAB trong tam giác ADB nên: \(\frac{{MD}}{{MB}} = \frac{{AD}}{{AB}} = \frac{{AD}}{{DC}}\)
Do đó, \(\frac{{NA}}{{NC}} = \frac{{MD}}{{MB}}\)
Suy ra: \(\frac{{NA}}{{MD}} = \frac{{NC}}{{MB}} = \frac{{NA + NC}}{{MD + MB}} = \frac{{AC}}{{BD}} = \frac{{AO}}{{DO}}\)
Do đó, \(\frac{{AN}}{{AO}} = \frac{{MD}}{{DO}}\)
Tam giác ADO có: \(\frac{{AN}}{{AO}} = \frac{{MD}}{{DO}}\) nên MN//AD (định lí Thalès đảo).
Bài 4 trang 48 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Bài tập yêu cầu học sinh phải hiểu rõ các định nghĩa, định lý liên quan đến hình thang cân để giải quyết các bài toán thực tế.
Bài 4 trang 48 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài 4 trang 48 sách bài tập Toán 8 - Chân trời sáng tạo tập 2, chúng ta sẽ đi vào phân tích từng phần của bài tập.
(Giả sử đề bài là: Cho hình thang cân ABCD (AB // CD), có AD = BC. Gọi E là giao điểm của AC và BD. Chứng minh rằng: a) ΔADE = ΔBCE; b) DE = EC.)
Đề bài yêu cầu chứng minh hai tam giác bằng nhau và chứng minh hai đoạn thẳng bằng nhau. Để chứng minh hai tam giác bằng nhau, chúng ta cần tìm ra các cặp cạnh tương ứng bằng nhau và góc tương ứng bằng nhau. Để chứng minh hai đoạn thẳng bằng nhau, chúng ta có thể sử dụng các tính chất của hình thang cân và các định lý đã học.
a) Chứng minh ΔADE = ΔBCE:
b) Chứng minh DE = EC:
Để củng cố kiến thức về hình thang cân, các em có thể làm thêm các bài tập tương tự sau:
Khi giải các bài tập về hình thang cân, các em cần lưu ý những điều sau:
Hy vọng với lời giải chi tiết và những lưu ý trên, các em sẽ tự tin hơn khi giải bài 4 trang 48 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 và các bài tập tương tự. Chúc các em học tốt!