Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 12 trang 93 sách bài tập Toán 8 - Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi và luyện tập để nắm vững kiến thức Toán 8 nhé!
Cho tấm bìa như Hình 1. Hùng xoay tấm bìa quanh tâm nó và quan sát xem khi tấm bìa dừng quay, mũi tên chỉ vào ô ghi số nào.
Đề bài
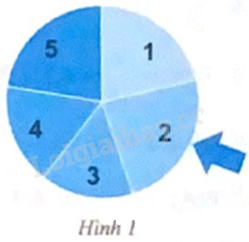
Cho tấm bìa như Hình 1. Hùng xoay tấm bìa quanh tâm nó và quan sát xem khi tấm bìa dừng quay, mũi tên chỉ vào ô ghi số nào. Hùng ghi lại kết quả của các lần xoay ở bảng sau:
Ô số | 1 | 2 | 3 | 4 | 5 |
Số lần | 34 | 38 | 25 | 27 | 36 |
a) Hãy tính xác suất thực nghiệm của các biến cố:
A: “Mũi tên chỉ vào ô ghi số 3”;
B: “Mũi tên chỉ vào ô ghi số chẵn”;
C: “Mũi tên chỉ vào ô ghi số lớn hơn 3”.
b) Nếu Hùng xoay tấm bìa 300 lần thì có khoảng bao nhiêu lần mũi tên chỉ vào ô ghi số 3.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về xác suất thực nghiệm của biến cố: Gọi P(A) là xác suất xuất hiện biến cố A khi thực hiện một phép thử. Gọi m(A) là số lần xuất hiện biến cố A khi thực hiện một phép thử đó m lần. Xác suất thực nghiệm của biến cố A là tỉ số \(\frac{{m\left( A \right)}}{m}\).
+ Sử dụng kiến thức về xác suất lí thuyết và xác suất thực nghiệm để tính: Giả sử xác suất của biến cố A là p. Khi thực hiện phép thử n lần thì số lần xuất hiện biến cố A sẽ gần bằng (nhưng không nhất thiết phải bằng) np.
Lời giải chi tiết
a) Tổng số lần quay là: \(34 + 38 + 25 + 27 + 36 = 160\)
Ta có 25 lần xảy ra biến cố A trong 160 lần thử nên xác suất thực nghiệm của các biến cố A sau 160 lần thử là: \(\frac{{25}}{{160}} = \frac{5}{{32}}\)
Ta có \(38 + 27 = 65\) lần xảy ra biến cố B trong 160 lần thử nên xác suất thực nghiệm của các biến cố B sau 160 lần thử là: \(\frac{{65}}{{160}} = \frac{{13}}{{32}}\)
Ta có \(27 + 36 = 63\) lần xảy ra biến cố C trong 160 lần thử nên xác suất thực nghiệm của các biến cố C sau 160 lần thử là: \(\frac{{63}}{{160}}\)
b) Vì Hùng xoay tấm bìa 300 lần nên số lần mũi tên chỉ vào ô ghi số 3 là: \(300.\frac{5}{{32}} \approx 47\) (lần)
Bài 12 trang 93 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Bài tập yêu cầu học sinh phải hiểu rõ các định lý, tính chất đã học để giải quyết các bài toán thực tế.
Bài 12 trang 93 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 12 trang 93 sách bài tập Toán 8 - Chân trời sáng tạo tập 2, chúng tôi xin trình bày lời giải chi tiết như sau:
(Giả sử đề bài là: Cho hình thang cân ABCD (AB // CD), có AB = 5cm, CD = 10cm, AD = 6cm. Tính độ dài đường cao AH của hình thang.)
Đề bài yêu cầu tính độ dài đường cao AH của hình thang cân ABCD. Để giải bài toán này, chúng ta cần sử dụng các tính chất của hình thang cân, đặc biệt là tính chất hai cạnh bên bằng nhau và hai góc kề một cạnh bên bằng nhau. Ngoài ra, chúng ta cũng cần sử dụng định lý Pitago để tính toán độ dài các đoạn thẳng.
Kẻ AH vuông góc với CD (H thuộc CD). Do ABCD là hình thang cân nên DH = (CD - AB) / 2 = (10 - 5) / 2 = 2.5cm.
Xét tam giác ADH vuông tại H, ta có: AH2 + DH2 = AD2 (định lý Pitago)
=> AH2 = AD2 - DH2 = 62 - 2.52 = 36 - 6.25 = 29.75
=> AH = √29.75 ≈ 5.45cm
Vậy độ dài đường cao AH của hình thang cân ABCD là khoảng 5.45cm.
Để giải các bài tập về hình thang cân một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
Các em có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Học Toán 8 đòi hỏi sự chăm chỉ, kiên trì và tư duy logic. Hãy dành thời gian ôn tập bài cũ, làm bài tập đầy đủ và tìm kiếm sự giúp đỡ của thầy cô giáo khi gặp khó khăn. Chúc các em học tập tốt!