Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 10 trang 64 sách bài tập Toán 8 - Chân trời sáng tạo tập 2. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp các bước giải dễ hiểu, kèm theo giải thích chi tiết để bạn nắm vững kiến thức. Hãy cùng giaitoan.edu.vn khám phá lời giải ngay nhé!
Trong Hình 10, cho biết \(AB = 4,2,IA = 6,IC = 10,\widehat {ABI} = {60^0}\), \(\widehat {CDx} = {120^0}\). Tính độ dài CD.
Đề bài
Trong Hình 10, cho biết \(AB = 4,2,IA = 6,IC = 10,\widehat {ABI} = {60^0}\), \(\widehat {CDx} = {120^0}\). Tính độ dài CD.
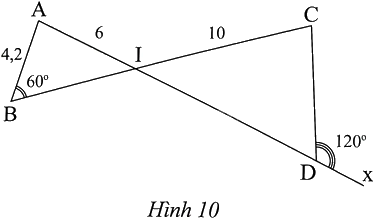
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g.g) để tính: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
Ta có: \(\widehat {CDI} = {180^0} - \widehat {CDx} = {60^0}\)
Tam giác ABI và tam giác CDI có: \(\widehat B = \widehat {CDI}\left( { = {{60}^0}} \right),\widehat {AIB} = \widehat {CID}\) (hai góc đối đỉnh)
Do đó, $\Delta ABI\backsim \Delta CDI\left( g.g \right)$. Suy ra: \(\frac{{AB}}{{CD}} = \frac{{AI}}{{CI}}\), hay \(\frac{{4,2}}{{CD}} = \frac{6}{{10}}\), suy ra \(CD = \frac{{4,2.10}}{6} = 7\)
Bài 10 trang 64 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Bài tập này yêu cầu học sinh phải hiểu rõ các định lý, tính chất đã học để giải quyết các bài toán thực tế.
Bài 10 trang 64 thường xoay quanh việc chứng minh một hình thang cân, tính độ dài các cạnh, đường cao hoặc các góc của hình thang cân. Đôi khi, bài tập còn yêu cầu học sinh sử dụng các công thức tính diện tích để giải quyết vấn đề.
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài tập. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, chúng ta có thể đưa ra một số hướng giải chung:
Giả sử bài tập yêu cầu chứng minh một hình thang cân. Chúng ta có thể sử dụng các tính chất sau:
Để củng cố kiến thức và kỹ năng giải bài tập hình thang cân, bạn có thể luyện tập thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. Hãy chú trọng vào việc hiểu rõ bản chất của bài toán và áp dụng các phương pháp giải phù hợp.
Hình học là một trong những phần quan trọng của chương trình Toán học. Việc học tốt hình học không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa mà còn phát triển tư duy logic, khả năng không gian và khả năng giải quyết vấn đề. Những kỹ năng này rất hữu ích trong cuộc sống và công việc.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục Toán học. Chúng tôi cung cấp các lời giải chi tiết, dễ hiểu, các bài tập luyện tập và các tài liệu tham khảo hữu ích. Hãy truy cập giaitoan.edu.vn để học Toán hiệu quả hơn!
| Tính chất | Mô tả |
|---|---|
| Hai cạnh bên bằng nhau | AB = CD |
| Hai góc kề một đáy bằng nhau | ∠A = ∠D, ∠B = ∠C |
| Hai đường chéo bằng nhau | AC = BD |