Bài 3 trang 63 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến các ứng dụng của hàm số bậc nhất. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về hàm số, cách xác định hệ số góc và tung độ gốc, cũng như khả năng vận dụng vào giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 trang 63 sách bài tập Toán 8 - Chân trời sáng tạo tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
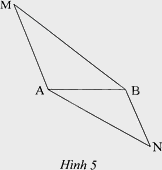
Cho tam giác MAB và ABN như Hình 5. Biết \(MA = 10cm,MB = 15cm,AB = 8cm,NA = 12cm,NB = 6,4cm\). Chứng minh rằng:
Đề bài
Cho tam giác MAB và ABN như Hình 5. Biết \(MA = 10cm,MB = 15cm,AB = 8cm,NA = 12cm,NB = 6,4cm\). Chứng minh rằng:
a) $\Delta MAB\backsim \Delta ABN$.
b) Tứ giác AMBN là hình thang.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về trường hợp đồng dạng thứ nhất của hai tam giác (c.c.c) để chứng minh: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
a) Xét tam giác MAB và tam giác ABN có: \(\frac{{MA}}{{AB}} = \frac{{AB}}{{BN}} = \frac{{MB}}{{AN}}\left( { = \frac{5}{4}} \right)\) Do đó, $\Delta MAB\backsim \Delta ABN\left( c.c.c \right)$
b) Vì $\Delta MAB\backsim \Delta ABN\left( cmt \right)$ nên \(\widehat {MAB} = \widehat {NBA}\), mà hai góc này ở vị trí so le trong nên MA//NB. Suy ra, tứ giác AMBN là hình thang.
Bài 3 trang 63 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc xác định hàm số bậc nhất biểu diễn mối quan hệ giữa hai đại lượng. Để giải bài toán này, chúng ta cần phân tích đề bài, xác định các yếu tố quan trọng và áp dụng các kiến thức đã học về hàm số bậc nhất.
Trước khi bắt đầu giải bài toán, chúng ta cần đọc kỹ đề bài và xác định rõ các thông tin sau:
Để giải bài toán này, chúng ta cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết bài 3 trang 63 sách bài tập Toán 8 - Chân trời sáng tạo tập 2:
(Nội dung lời giải chi tiết bài toán sẽ được trình bày tại đây, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Ví dụ: Giả sử đề bài cho một bảng số liệu về quãng đường đi được của một chiếc xe theo thời gian. Lời giải sẽ hướng dẫn học sinh cách xác định hai điểm thuộc đồ thị hàm số, tính hệ số góc a và tung độ gốc b, từ đó xác định được hàm số bậc nhất biểu diễn mối quan hệ giữa quãng đường và thời gian.)
Để giúp các em học sinh hiểu rõ hơn về cách giải bài toán, chúng ta cùng xem xét một ví dụ minh họa sau:
(Nội dung ví dụ minh họa sẽ được trình bày tại đây, bao gồm một bài toán tương tự bài 3 trang 63, nhưng có số liệu khác. Lời giải sẽ được trình bày chi tiết, giúp học sinh tự tin áp dụng vào giải bài toán gốc.)
Để rèn luyện kỹ năng giải bài toán, các em học sinh có thể tự giải các bài tập tương tự sau:
Khi giải bài toán về hàm số bậc nhất, các em học sinh cần lưu ý những điều sau:
Bài 3 trang 63 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Hy vọng với lời giải chi tiết và ví dụ minh họa trên, các em học sinh sẽ hiểu rõ phương pháp giải và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục môn Toán. Chúc các em học tập tốt!