Bài 6 trang 45 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các phép biến đổi đại số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 45 sách bài tập Toán 8 - Chân trời sáng tạo tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM//QO\(\left( {M \in OP} \right)\), IN//PO \(\left( {N \in QO} \right)\). Chứng minh:
Đề bài
Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM//QO\(\left( {M \in OP} \right)\), IN//PO \(\left( {N \in QO} \right)\). Chứng minh:
a) Tam giác IMN cân tại I.
b) OI là đường trung trực của MN.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về đường trung bình của tam giác để chứng minh: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
+ Sử dụng kiến thức về tính chất của đường trung bình của tam giác để chứng minh: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết
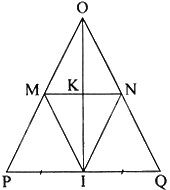
a) Tam giác OPQ có: \(IP = IQ\), IM//QO nên \(MO = MP\)
Tam giác OPQ có: \(IP = IQ\), \(MO = MP\) nên IM là đường trung bình của tam giác OPQ, suy ra \(IM = \frac{1}{2}QO\)
Tương tự ta có: \(IN = \frac{1}{2}PO\).
Mà \(PO = QO\) (do tam giác POQ cân tại O) nên \(IM = IN\), suy ra tam giác IMN cân tại I.
b) Gọi K là giao điểm của IO và MN.
Tam giác OPQ có: \(MO = MP\), \(NO = NQ\) nên MN là đường trung bình của tam giác OPQ, suy ra MN//PQ (1).
Tam giác OPQ cân tại O có OI là đường trung tuyến nên OI cũng là đường cao của tam giác OPQ.
Suy ra: \(OI \bot PQ\) (2)
Từ (1) và (2) suy ra: \(MN \bot OI\) tại K hay \(MN \bot IK\)
Mà tam giác IMN cân tại I nên IK là đường trung trực của MN hay OI là đường trung trực của MN.
Bài 6 trang 45 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học về các phép biến đổi đại số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản như:
Dưới đây là đề bài và lời giải chi tiết bài 6 trang 45 sách bài tập Toán 8 - Chân trời sáng tạo tập 2:
(Đề bài cụ thể của bài 6 trang 45 sẽ được chèn vào đây. Ví dụ: Phân tích các đa thức sau thành nhân tử: a) x2 - 4; b) x2 + 2x + 1; c) 4x2 - 9)
a) x2 - 4
Áp dụng hằng đẳng thức hiệu hai bình phương: a2 - b2 = (a - b)(a + b)
Ta có: x2 - 4 = x2 - 22 = (x - 2)(x + 2)
b) x2 + 2x + 1
Áp dụng hằng đẳng thức bình phương của một tổng: (a + b)2 = a2 + 2ab + b2
Ta có: x2 + 2x + 1 = x2 + 2.x.1 + 12 = (x + 1)2
c) 4x2 - 9
Áp dụng hằng đẳng thức hiệu hai bình phương: a2 - b2 = (a - b)(a + b)
Ta có: 4x2 - 9 = (2x)2 - 32 = (2x - 3)(2x + 3)
Kết luận:
Để hiểu rõ hơn về cách giải các bài tập phân tích đa thức thành nhân tử, các em có thể tham khảo thêm các bài giảng và tài liệu học tập khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Ngoài ra, các em có thể sử dụng các công cụ hỗ trợ giải toán online để kiểm tra lại kết quả của mình. Tuy nhiên, việc tự mình giải bài tập vẫn là cách học hiệu quả nhất.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết bài 6 trang 45 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 này sẽ giúp các em học sinh học tập tốt hơn. Chúc các em thành công!
Các bài tập tương tự:
Lưu ý:
Lời giải trên chỉ mang tính chất tham khảo. Các em nên tự mình giải bài tập để hiểu rõ hơn về kiến thức và rèn luyện kỹ năng giải toán.
| Hằng đẳng thức | Công thức |
|---|---|
| Bình phương của một tổng | (a + b)2 = a2 + 2ab + b2 |
| Bình phương của một hiệu | (a - b)2 = a2 - 2ab + b2 |
| Hiệu hai bình phương | a2 - b2 = (a - b)(a + b) |