Giải bài 1 trang 60 Sách bài tập Toán 8 - Chân trời sáng tạo

Giải bài 1 trang 60 sách bài tập toán 8 - Chân trời sáng tạo

Giải bài 1 trang 60 Sách bài tập Toán 8 - Chân trời sáng tạo

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 sách Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 1 trang 60, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.

Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán.

Cho tứ giác ABCD có \(AB = BC\) và AC là tia phân giác của góc A. Chứng minh tứ giác ABCD là hình thang.

Đề bài

Cho tứ giác ABCD có \(AB = BC\) và AC là tia phân giác của góc A. Chứng minh tứ giác ABCD là hình thang.

Phương pháp giải - Xem chi tiết Giải bài 1 trang 60 sách bài tập toán 8 - Chân trời sáng tạo 1

Sử dụng kiến thức về dấu hiệu nhận biết hình thang để chứng minh: Tứ giác có hai cạnh đối song song là hình thang.

Lời giải chi tiết

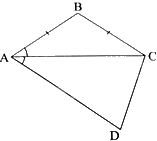
Giải bài 1 trang 60 sách bài tập toán 8 - Chân trời sáng tạo 2

Tam giác ABC có: \(AB = BC\) nên tam giác ABC cân tại B. Do đó, \(\widehat {BAC} = \widehat {BCA}\)

Vì AC là tia phân giác của góc BAD nên \(\widehat {BAC} = \widehat {CAD}\)

Do đó, \(\widehat {CAD} = \widehat {BCA}\), mà hai góc này ở vị trí so le trong nên BC//AD

Tứ giác ABCD có: BC//AD nên tứ giác ABCD là hình thang.

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 1 trang 60 sách bài tập toán 8 - Chân trời sáng tạo đặc sắc thuộc chuyên mục bài tập sách giáo khoa toán 8 trên môn toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 1 trang 60 Sách bài tập Toán 8 - Chân trời sáng tạo: Tổng quan

Bài 1 trang 60 sách bài tập Toán 8 Chân trời sáng tạo thuộc chương trình học về các phép biến đổi đơn giản với đa thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về thu gọn đa thức, tìm bậc của đa thức và xác định hệ số của đa thức. Việc nắm vững các khái niệm này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.

Nội dung bài 1 trang 60 Sách bài tập Toán 8 - Chân trời sáng tạo

Bài 1 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh thực hiện các thao tác sau:

Thu gọn các đa thức đã cho.
Xác định bậc của mỗi đa thức sau khi thu gọn.
Tìm hệ số của các hạng tử trong đa thức.

Hướng dẫn giải chi tiết bài 1 trang 60 Sách bài tập Toán 8 - Chân trời sáng tạo

Câu a)

Đa thức cần thu gọn: 3x² - 2x + 5x⁴ - 3x² + 1

Thu gọn các hạng tử đồng dạng: 3x² - 3x² = 0
Đa thức sau khi thu gọn: 5x⁴ - 2x + 1
Bậc của đa thức: 4 (là số mũ lớn nhất của biến x)
Hệ số của x⁴: 5
Hệ số của x: -2
Hệ số tự do: 1

Câu b)

Đa thức cần thu gọn: 1/2 x³ + 2x² - x + 1/2 x³ - 3x²

Thu gọn các hạng tử đồng dạng: 1/2 x³ + 1/2 x³ = x³; 2x² - 3x² = -x²
Đa thức sau khi thu gọn: x³ - x² - x
Bậc của đa thức: 3
Hệ số của x³: 1
Hệ số của x²: -1
Hệ số của x: -1

Câu c)

Đa thức cần thu gọn: 4x² - 3x + x² - 5 + 2x - x²

Thu gọn các hạng tử đồng dạng: 4x² + x² - x² = 4x²; -3x + 2x = -x
Đa thức sau khi thu gọn: 4x² - x - 5
Bậc của đa thức: 2
Hệ số của x²: 4
Hệ số của x: -1
Hệ số tự do: -5

Lưu ý khi giải bài tập về đa thức

Luôn thu gọn đa thức trước khi xác định bậc và hệ số.
Chú ý các dấu âm và dương khi cộng trừ các hạng tử đồng dạng.
Kiểm tra lại kết quả sau khi giải để đảm bảo tính chính xác.

Ứng dụng của việc giải bài tập về đa thức

Việc giải bài tập về đa thức không chỉ giúp học sinh nắm vững kiến thức về đa thức mà còn là nền tảng để giải quyết các bài toán phức tạp hơn trong chương trình Toán học. Kỹ năng thu gọn đa thức, tìm bậc của đa thức và xác định hệ số của đa thức được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như vật lý, hóa học, kinh tế học và khoa học máy tính.

Tổng kết

Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 1 trang 60 sách bài tập Toán 8 Chân trời sáng tạo. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình. Chúc bạn học tập tốt!