Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 8 trang 19 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp học sinh hiểu bài và làm bài tập một cách hiệu quả.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, chính xác và dễ hiểu nhất để hỗ trợ các em học sinh trong quá trình học tập môn Toán.
Đoạn thẳng trong hình vẽ bên là tập hợp những điểm (x; y) thỏa mãn điều kiện nào dưới đây? A. \( - 1 \le y \le 3\) và \(x = 2\). B. \( - 1 \le x \le 3\) và \(y \le 2\). C. \( - 1 \le x \le 3\) và \(y = 2\). D. \(x \ge - 1\) và \(y = 2\).
Đề bài
Đoạn thẳng trong hình vẽ bên là tập hợp những điểm (x; y) thỏa mãn điều kiện nào dưới đây?
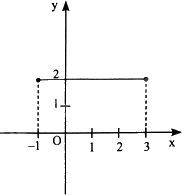
A. \( - 1 \le y \le 3\) và \(x = 2\).
B. \( - 1 \le x \le 3\) và \(y \le 2\).
C. \( - 1 \le x \le 3\) và \(y = 2\).
D. \(x \ge - 1\) và \(y = 2\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về đồ thị hàm số để tìm đáp án đúng: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\)
Lời giải chi tiết
Nhìn vào đồ thị ta thấy cặp số (x; y) thỏa mãn điều kiện: \( - 1 \le x \le 3\) và \(y = 2\)
Chọn C
Bài 8 trang 19 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức đã học về các phép biến đổi đơn giản với phân thức đại số. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như phân thức, điều kiện xác định của phân thức, và các quy tắc cộng, trừ, nhân, chia phân thức.
Bài 8 bao gồm một số câu hỏi và bài tập yêu cầu học sinh thực hiện các phép toán với phân thức. Cụ thể, các em sẽ cần:
Để rút gọn phân thức, ta cần phân tích tử thức và mẫu thức thành nhân tử. Sau đó, ta tìm các nhân tử chung của tử thức và mẫu thức và chia cả tử và mẫu cho nhân tử chung đó. Ví dụ, nếu ta có phân thức A/B, và cả tử và mẫu đều chia hết cho C, thì ta có thể rút gọn phân thức thành (A/C) / (B/C).
Để quy đồng mẫu số của các phân thức, ta cần tìm mẫu số chung nhỏ nhất (MSC) của các phân thức. Sau đó, ta nhân cả tử và mẫu của mỗi phân thức với một số sao cho mẫu số của chúng bằng MSC. Ví dụ, nếu ta có hai phân thức A/B và C/D, và MSC là M, thì ta sẽ quy đồng hai phân thức thành (A * (M/B)) / M và (C * (M/D)) / M.
Các phép cộng, trừ, nhân, chia phân thức được thực hiện tương tự như các phép toán với số. Tuy nhiên, trước khi thực hiện các phép toán, ta cần đảm bảo rằng các phân thức có cùng mẫu số (đối với phép cộng và trừ) hoặc mẫu số khác 0 (đối với phép nhân và chia).
Giả sử ta có phân thức (x^2 - 1) / (x + 1). Để rút gọn phân thức này, ta phân tích tử thức thành nhân tử: x^2 - 1 = (x - 1)(x + 1). Sau đó, ta chia cả tử và mẫu cho x + 1, ta được phân thức rút gọn là x - 1.
Khi giải bài tập về phân thức, học sinh cần chú ý đến điều kiện xác định của phân thức. Mẫu số của phân thức không được bằng 0. Nếu mẫu số bằng 0, phân thức không xác định.
Để củng cố kiến thức và kỹ năng giải bài tập về phân thức, học sinh có thể tự giải thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác.
Bài 8 trang 19 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về phân thức. Bằng cách nắm vững lý thuyết, phương pháp giải và thực hành giải nhiều bài tập, các em sẽ có thể tự tin giải quyết các bài toán tương tự trong các kỳ thi và bài kiểm tra.
| Phân thức | Điều kiện xác định |
|---|---|
| A/B | B ≠ 0 |