Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 4 trang 60 sách bài tập Toán 8 Chân trời sáng tạo. Chúng tôi hiểu rằng việc giải bài tập có thể gặp nhiều khó khăn, vì vậy chúng tôi luôn cố gắng trình bày các bước giải một cách rõ ràng và logic nhất.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức Toán 8, tự tin giải quyết các bài tập và đạt kết quả tốt trong học tập.
Hình thang ABCD (AB//CD) có \(\widehat {ACD} = \widehat {BDC}\). Chứng minh tứ giác ABCD là hình thang cân.
Đề bài
Hình thang ABCD (AB//CD) có \(\widehat {ACD} = \widehat {BDC}\). Chứng minh tứ giác ABCD là hình thang cân.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về dấu hiệu nhận biết hình thang cân để chứng minh: Hình thang có hai đường chéo bằng nhau là hình thang cân.
Lời giải chi tiết
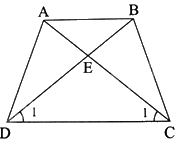
Gọi E là giao điểm của AC và BD.
Tam giác EDC có: \(\widehat {{C_1}} = \widehat {{D_1}}\) nên tam giác EDC cân tại E. Do đó, \(EC = DE\) (1)
Vì AB//CD nên \(\widehat {{D_1}} = \widehat {EBA};\widehat {{C_1}} = \widehat {EAB}\)
Mà \(\widehat {{C_1}} = \widehat {{D_1}}\) nên \(\widehat {EAB} = \widehat {ABE}\)
Do đó, tam giác ABE cân tại E. Do đó: \(EA = EB\) (2)
Từ (1) và (2) ta có: \(EC + AE = DE + EB\)
Suy ra: \(AC = BD\)
Hình thang ABCD có: \(AC = BD\) nên tứ giác ABCD là hình thang cân.
Bài 4 trang 60 sách bài tập Toán 8 Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Bài tập này yêu cầu học sinh phải hiểu rõ các định nghĩa, định lý và tính chất của các hình này để giải quyết các bài toán liên quan đến tính độ dài đoạn thẳng, số đo góc và diện tích.
Bài 4 trang 60 thường bao gồm các dạng bài tập sau:
Giả sử bài 4 yêu cầu tính độ dài đường chéo của một hình chữ nhật có chiều dài 8cm và chiều rộng 6cm. Để giải bài này, ta sử dụng định lý Pitago trong tam giác vuông tạo bởi chiều dài, chiều rộng và đường chéo của hình chữ nhật. Đường chéo sẽ là cạnh huyền của tam giác vuông đó.
Áp dụng định lý Pitago, ta có: Đường chéo2 = Chiều dài2 + Chiều rộng2 = 82 + 62 = 64 + 36 = 100
Vậy, Đường chéo = √100 = 10cm.
Để hiểu sâu hơn về các hình bình hành, hình chữ nhật, hình thoi và hình vuông, bạn có thể tìm hiểu thêm về:
Giaitoan.edu.vn là một nguồn tài liệu học Toán 8 uy tín và chất lượng. Chúng tôi cung cấp đầy đủ các lời giải bài tập, các bài giảng video, các bài kiểm tra và các tài liệu tham khảo khác để giúp bạn học Toán 8 một cách hiệu quả nhất. Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều tài liệu hữu ích khác!
| Hình | Công thức tính diện tích |
|---|---|
| Hình bình hành | S = h * a (h là chiều cao, a là cạnh đáy) |
| Hình chữ nhật | S = a * b (a là chiều dài, b là chiều rộng) |
| Hình thoi | S = (d1 * d2) / 2 (d1, d2 là độ dài hai đường chéo) |
| Hình vuông | S = a2 (a là cạnh) |