Chào mừng các em học sinh đến với lời giải chi tiết bài 9 trang 75 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 8.
Chúng tôi sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để các em hiểu rõ bản chất của bài toán.
Cho tam giác ABC vuông tại A và đường cao AH. a) Chứng minh rằng \(A{B^2} = BH.BC\).
Đề bài
Cho tam giác ABC vuông tại A và đường cao AH.
a) Chứng minh rằng \(A{B^2} = BH.BC\).
b) Chứng minh rằng \(A{H^2} = BH.CH\).
c) Trên tia đối của tia AC lấy điểm D \(\left( {AD < AC} \right)\). Đường thẳng qua H và song song với AC cắt AB, BD lần lượt tại M, N. Chứng minh rằng \(\frac{{MN}}{{MH}} = \frac{{AD}}{{AC}}\).
d) Vẽ AE vuông góc với BD tại E. Chứng minh rằng \(\widehat {BEH} = \widehat {BAH}\).
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g.g) để tính: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
+ Sử dụng kiến thức về trường hợp đồng dạng thứ hai của hai tam giác (c.g.c) để tính chứng minh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
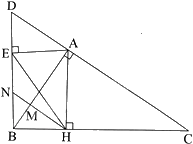
a) Chứng minh được $\Delta ABC\backsim \Delta HBA\left( g.g \right)$ nên \(\frac{{AB}}{{HB}} = \frac{{BC}}{{AB}}\), do đó, \(A{B^2} = BH.BC\)
b) Chứng minh được $\Delta HBA\backsim \Delta HAC\left( g.g \right)$ nên \(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\), do đó \(A{H^2} = BH.CH\).
c) Tam giác ABD có MN//AD nên \(\frac{{MN}}{{AD}} = \frac{{BM}}{{BA}}\left( 1 \right)\)
Tam giác ABC có MH//AC nên \(\frac{{MH}}{{AC}} = \frac{{BM}}{{BA}}\left( 2 \right)\)
Từ (1) và (2) ta có: \(\frac{{MN}}{{AD}} = \frac{{MH}}{{AC}}\) hay \(\frac{{MN}}{{MH}} = \frac{{AD}}{{AC}}\)
d) Chứng minh được $\Delta ABD\backsim \Delta EBA\left( g.g \right)$, suy ra \(\frac{{AB}}{{BE}} = \frac{{BD}}{{AB}}\) hay \(A{B^2} = BE.BD\)
Mà \(A{B^2} = BH.BC\) nên \(BE.BD = BH.BC\), hay \(\frac{{BH}}{{BD}} = \frac{{BE}}{{BC}}\)
Xét tam giác BEH và tam giác BCD ta có: \(\frac{{BH}}{{BD}} = \frac{{BE}}{{BC}}\) góc DBC chung. Do đó, $\Delta BEH\backsim \Delta BCD\left( c.g.c \right)$
Suy ra \(\widehat {BEH} = \widehat {BCD}\). Mà \(\widehat {BAH} = \widehat {BCD}\) (cùng phụ với góc HAC). Vậy \(\widehat {BEH} = \widehat {BAH}\)
Bài 9 trang 75 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân và ứng dụng vào giải quyết các bài toán thực tế.
Để giải bài 9 trang 75, chúng ta cần xem xét kỹ đề bài và áp dụng các kiến thức đã học về hình thang cân. Dưới đây là giải chi tiết từng phần của bài toán:
(Nội dung câu a của bài 9 sẽ được giải thích chi tiết ở đây, bao gồm các bước giải, công thức sử dụng và kết quả cuối cùng.)
(Nội dung câu b của bài 9 sẽ được giải thích chi tiết ở đây, bao gồm các bước giải, công thức sử dụng và kết quả cuối cùng.)
(Nội dung câu c của bài 9 sẽ được giải thích chi tiết ở đây, bao gồm các bước giải, công thức sử dụng và kết quả cuối cùng.)
Để giúp các em hiểu rõ hơn về cách giải bài tập hình thang cân, chúng ta cùng xem xét một ví dụ minh họa sau:
Bài tập: Cho hình thang cân ABCD (AB // CD), AB = 10cm, CD = 20cm, AD = BC = 13cm. Tính chiều cao của hình thang.
Giải:
Để củng cố kiến thức và kỹ năng giải bài tập về hình thang cân, các em có thể tự giải thêm các bài tập sau:
Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em đã hiểu rõ cách giải bài 9 trang 75 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!