Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 sách Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 3 trang 57, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán.
Cho tứ giác ABCD như Hình 12. a) Tính độ dài hai đường chéo và cạnh còn lại của tứ giác ABCD.
Đề bài
Cho tứ giác ABCD như Hình 12.
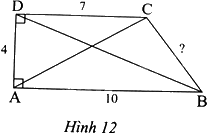
a) Tính độ dài hai đường chéo và cạnh còn lại của tứ giác ABCD.
b) Cho biết góc B bằng \({53^0}\). Tìm số đo góc C.
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về định lí Pythagore vào tam giác vuông để tính: Trong một tam giác vuông, bình vuông độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.
b) Sử dụng kiến thức về tổng các góc của một tứ giác để tính góc C: Tổng số đo các góc của một tứ giác bằng 360 độ.
Lời giải chi tiết
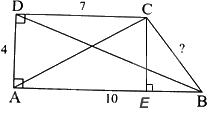
a) Áp dụng định lí Pythagore vào tam giác ADC vuông tại D có:
\(A{C^2} = A{D^2} + D{C^2} = {4^2} + {7^2} = 65\), suy ra \(AC = \sqrt {65} \)
Áp dụng định lí Pythagore vào tam giác ADB vuông tại A có:
\(B{D^2} = A{D^2} + A{B^2} = {4^2} + {10^2} = 116\), suy ra \(BD = \sqrt {116} \)
Kẻ CE \( \bot \) AB. Do AD \( \bot \) AB suy ra CE // AD.
Suy ra \(\widehat {DAC} = \widehat {ACE}\) (hai góc so le trong)
Xét \(\Delta ADC\) và \(\Delta CEA\) có:
\(\widehat D = \widehat E = {90^o}\)
\(\widehat {DAC} = \widehat {ACE}\)(cmt)
AC chung
=> \(\Delta ADC\) = \(\Delta CEA\) (cạnh huyền – góc nhọn)
=> AD = CE = 4, DC = AE = 7 (các cặp cạnh tương ứng)
Ta có AE + EB = AB => EB = AB – AE = 10 – 7 = 3
Áp dụng định lí Pythagore vào tam giác CEB vuông tại E, ta có:
\(C{E^2} + E{B^2} = {4^2} + {3^2} = 25 = {5^2} = B{C^2}\), suy ra BC = 5
b) Tứ giác ABCD có: \(\widehat {DCB} = {360^0} - \widehat {DAB} - \widehat {ADC} - \widehat {ABC} = {360^0} - {90^0} - {90^0} - {53^0} = {127^0}\)
Bài 3 trang 57 sách bài tập Toán 8 Chân trời sáng tạo thuộc chương trình học về các hình khối trong không gian, cụ thể là hình lăng trụ đứng và hình chóp. Bài tập này yêu cầu học sinh vận dụng kiến thức về diện tích xung quanh, diện tích đáy và thể tích của các hình này để giải quyết các bài toán thực tế.
Bài 3 thường bao gồm các dạng bài tập sau:
Để giải bài 3 trang 57 một cách hiệu quả, bạn cần nắm vững các công thức sau:
Để giúp bạn hiểu rõ hơn, chúng ta sẽ cùng nhau giải chi tiết từng phần của bài 3 trang 57:
Bước 1: Xác định chu vi đáy của hình lăng trụ đứng. Ví dụ, nếu đáy là hình vuông có cạnh 5cm, thì chu vi đáy là 5cm * 4 = 20cm.
Bước 2: Xác định chiều cao của hình lăng trụ đứng. Ví dụ, chiều cao là 8cm.
Bước 3: Áp dụng công thức tính diện tích xung quanh: Diện tích xung quanh = Chu vi đáy * Chiều cao = 20cm * 8cm = 160cm2.
Bước 1: Tính diện tích đáy của hình chóp. Ví dụ, nếu đáy là hình tam giác vuông có hai cạnh góc vuông là 3cm và 4cm, thì diện tích đáy là (1/2) * 3cm * 4cm = 6cm2.
Bước 2: Xác định chiều cao của hình chóp. Ví dụ, chiều cao là 5cm.
Bước 3: Áp dụng công thức tính thể tích: Thể tích = (1/3) * Diện tích đáy * Chiều cao = (1/3) * 6cm2 * 5cm = 10cm3.
Để giải nhanh các bài tập về hình lăng trụ đứng và hình chóp, bạn nên:
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự sau:
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 3 trang 57 sách bài tập Toán 8 Chân trời sáng tạo. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất trong học tập. Chúc bạn thành công!