Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 59 sách bài tập Toán 8 Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu bài và làm bài tập một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy cùng chúng tôi khám phá lời giải bài tập này ngay bây giờ!
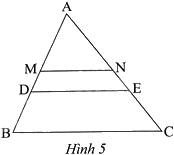
Trong Hình 5, cho biết MN là đường trung bình của tam giác ABC. Tam giác ADE đồng dạng với tam giác ABC theo tỉ số \(k = \frac{2}{3}\).
Đề bài
Trong Hình 5, cho biết MN là đường trung bình của tam giác ABC. Tam giác ADE đồng dạng với tam giác ABC theo tỉ số \(k = \frac{2}{3}\).
a) Chứng minh rằng $\Delta ADE\backsim \Delta AMN$.
b) Tính tỉ số đồng dạng của tam giác ADE và tam giác AMN.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về định lí về hai tam giác đồng dạng: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
+ Sử dụng kiến thức về tính chất của hai tam giác đồng dạng để chứng minh: Nếu $\Delta A'B'C'\backsim \Delta A''B''C''$ và $\Delta A''B''C''\backsim \Delta ABC$ thì $\Delta A'B'C'\backsim \Delta ABC$
Lời giải chi tiết
a) Vì MN là đường trung bình của tam giác ABC nên MN//BC. Do đó,
Theo giả thiết, \(\Delta ADE\backsim \Delta ABC\) nên $\Delta ADE\backsim \Delta AMN$
b) \(\Delta ADE\backsim \Delta ABC\) theo tỉ số đồng dạng \(\frac{{AD}}{{AB}} = \frac{2}{3}\)
$\Delta ABC\backsim \Delta AMN$ theo tỉ số đồng dạng \(\frac{{AB}}{{AM}} = 2\)
Do đó, \(\frac{{AD}}{{AB}}.\frac{{AB}}{{AM}} = \frac{2}{3}.2\), suy ra \(\frac{{AD}}{{AM}} = \frac{4}{3}\)
Do đó, $\Delta ADE\backsim \Delta AMN$ theo tỉ số đồng dạng \(\frac{4}{3}\).
Bài 2 trang 59 sách bài tập Toán 8 Chân trời sáng tạo tập 2 thuộc chương trình học về các tứ giác đặc biệt. Để giải bài tập này, học sinh cần nắm vững kiến thức về:
Bài tập 2 yêu cầu học sinh xác định các hình thang cân và hình bình hành trong một hình vẽ cho trước, dựa trên các thông tin về độ dài cạnh và số đo góc. Bài tập này rèn luyện khả năng vận dụng các tính chất của các tứ giác đặc biệt để giải quyết vấn đề.
Để giải bài tập này, chúng ta sẽ tiến hành theo các bước sau:
Ví dụ minh họa (giả sử hình vẽ có các điểm A, B, C, D):
Nếu AB // CD và AD = BC, thì tứ giác ABCD là hình thang cân.
Nếu AB // CD và AB = CD, thì tứ giác ABCD là hình bình hành.
Để giải các bài tập tương tự, học sinh cần:
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Các em có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 8:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh đã hiểu rõ cách giải bài 2 trang 59 sách bài tập Toán 8 Chân trời sáng tạo tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!