Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 10 sách bài tập Toán 8 Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu bài và làm bài tập một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy cùng chúng tôi khám phá lời giải bài tập này ngay bây giờ!
Tìm tọa độ của các điểm A, B, C, D, E trong Hình 8.
Đề bài
Tìm tọa độ của các điểm A, B, C, D, E trong Hình 8.
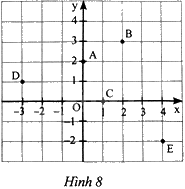
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức tọa độ của một điểm trong mặt phẳng tọa độ: Ta xác định vị trí của điểm P trong mặt phẳng tọa độ Oxy bằng cách sau: Từ P vẽ các đường vuông góc với các trục tọa độ cắt trục hoành tại điểm a và trục tung tại điểm b. Khi đó cặp số (a; b) gọi là tọa độ của điểm P và kí hiệu P (a; b). Số a gọi là hoành độ và số b gọi là tung độ của điểm P.
Lời giải chi tiết
\(A\left( {0;2} \right);B\left( {2;3} \right);C\left( {1;0} \right);D\left( { - 3;1} \right);E\left( {4; - 2} \right)\)
Bài 1 trang 10 sách bài tập Toán 8 Chân trời sáng tạo tập 2 thuộc chương trình học về các phép biến đổi đơn giản với đa thức. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài tập yêu cầu học sinh thực hiện các phép toán đơn giản với đơn thức và đa thức, đồng thời áp dụng các hằng đẳng thức để rút gọn biểu thức.
Dưới đây là lời giải chi tiết cho từng phần của bài 1:
Đề bài: Thực hiện phép tính: 3x2 + 2x - 5 + x2 - 3x + 2
Lời giải:
3x2 + 2x - 5 + x2 - 3x + 2 = (3x2 + x2) + (2x - 3x) + (-5 + 2) = 4x2 - x - 3
Đề bài: Thực hiện phép tính: 5xy - 2x2 + 3xy + x2 - 4
Lời giải:
5xy - 2x2 + 3xy + x2 - 4 = (5xy + 3xy) + (-2x2 + x2) - 4 = 8xy - x2 - 4
Đề bài: Thực hiện phép tính: (x2 - 2x + 1) - (x2 + x - 3)
Lời giải:
(x2 - 2x + 1) - (x2 + x - 3) = x2 - 2x + 1 - x2 - x + 3 = (x2 - x2) + (-2x - x) + (1 + 3) = -3x + 4
Để giải các bài tập tương tự, học sinh cần:
Thực hiện phép tính: 2x3 - 5x2 + 3x + 1 - (x3 + 2x2 - x + 5)
Lời giải:
2x3 - 5x2 + 3x + 1 - (x3 + 2x2 - x + 5) = 2x3 - 5x2 + 3x + 1 - x3 - 2x2 + x - 5 = (2x3 - x3) + (-5x2 - 2x2) + (3x + x) + (1 - 5) = x3 - 7x2 + 4x - 4
Để củng cố kiến thức và kỹ năng giải bài tập, học sinh có thể tự luyện tập thêm với các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác.
Bài 1 trang 10 sách bài tập Toán 8 Chân trời sáng tạo tập 2 là một bài tập cơ bản về các phép toán với đơn thức và đa thức. Việc nắm vững lý thuyết và phương pháp giải sẽ giúp học sinh giải quyết bài tập một cách nhanh chóng và chính xác. Chúc các em học tập tốt!